Qiskitで勾配降下法を実装してみる

モチベーション

qiskitのgraidient FW がいまいち動作が遅いようだったので、自分で組んでみます。
https://qiita.com/notori48/items/905f55bc7215fdd05817

ここでは最小限のものしか組みませんが、応用すると色々な回路で勾配降下出来ると思います。
Pennylaneのチュートリアルを見ると良いでしょう。
https://pennylane.ai/qml/glossary/parameter_shift.html

サンプル問題

パウリ$Z$の期待値を最小化してみます。明らかに最小値は-1です。

実装

先人のコピペをベースにします。
https://www.investor-daiki.com/it/qiskit-parameter-shift

ただしqiskit.aquaはもう廃止になっているので、import先を読み替えています。
https://qiskit.org/documentation/aqua_tutorials/Qiskit%20Algorithms%20Migration%20Guide.html#QuantumInstance

from qiskit import Aer
from qiskit.circuit import QuantumCircuit, ParameterVector
from qiskit.utils import QuantumInstance
from qiskit.opflow import I,X, Y, Z, StateFn, CircuitStateFn
from qiskit.opflow.expectations import PauliExpectation, AerPauliExpectation
from qiskit.opflow.converters import CircuitSampler

import numpy as np
%matplotlib inline

てきとーな変分回路を作り、1量子ビット目の$Z$期待値を取ります。

# インスタンスを定義
backend = Aer.get_backend('qasm_simulator') 
q_instance = QuantumInstance(backend, shots=1024)

# ハミルトニアンの期待値
def cost_function(params):
    n = 3 # num of paramers per layers
    qc = QuantumCircuit(n)
    param_list = ParameterVector('Parameter', 2*n) #two layers

    for i in range(len(param_list)//n):
        qc.rx(param_list[3*i], 0)
        qc.ry(param_list[3*i+1], 1)
        qc.rz(param_list[3*i+2], 2)

        qc.cnot(0, 1)
        qc.cnot(1, 2)
        qc.cnot(2, 0)

    param_dict = dict(zip(param_list.params, params))
    qc.assign_parameters(param_dict, inplace=True)

    op = Z ^ I ^ I # ハミルトニアンを定義
    psi = CircuitStateFn(qc) # 状態ベクトルを定義
    measurable_expression = StateFn(op, is_measurement=True).compose(psi) 

    # 期待値を計算
    expectation = AerPauliExpectation().convert(measurable_expression)
    sampler = CircuitSampler(q_instance).convert(expectation) 

    return sampler.eval().real

cost_function(params=[1, 0.5, -0.765, 0.1, 0, -0.654])
0.8731983044562818

勾配なし最適化

from scipy.optimize import minimize
import time
np.random.seed(0)

var_init = np.random.uniform(low=-1, high=1, size=(2*3)) # one-dimensional array
hist_cost = []
var = var_init

count = 0
def cbf(Xi):
    global count
    global hist_cost
    cost_now = cost_function(Xi)
    hist_cost.append(cost_now)
    print('iter = '+str(count)+' | cost = '+str(cost_now))
    count += 1


t1 = time.time()
result = minimize(fun=cost_function, x0=var_init, method='Nelder-Mead', callback=cbf, options={"maxiter":100})
# 処理後の時刻
t2 = time.time() 
# 経過時間を表示
elapsed_time = t2-t1
print(f"経過時間：{elapsed_time}")

iter = 0 | cost = 0.8855733931478532
iter = 1 | cost = 0.8855733931478532
iter = 2 | cost = 0.8855733931478532
iter = 3 | cost = 0.8855733931478532
iter = 4 | cost = 0.8787580617400559
iter = 5 | cost = 0.8787580617400559
...
iter = 93 | cost = -0.96745572333234
iter = 94 | cost = -0.9677905905486676
iter = 95 | cost = -0.9698397198474791
iter = 96 | cost = -0.9720836918454269
iter = 97 | cost = -0.9764200253312859
iter = 98 | cost = -0.9764200253312859
経過時間：4.2200000286102295

import matplotlib.pyplot as plt
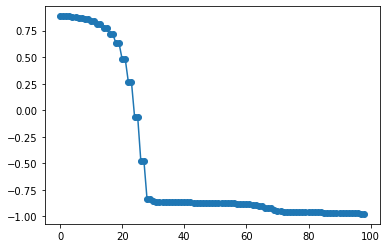
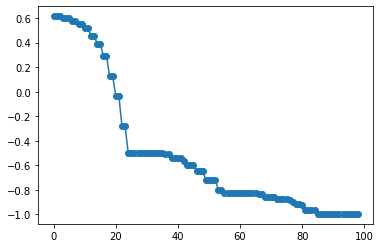
plt.plot(hist_cost,'o-')

期待通り-1に収束していますが、30 iterations　要しています。
初期値を変えて何度かやってみます。

最低 20 iterations かかるようです。

勾配降下

勾配はparameter-shift rule により実装します。

def my_grad(params):
    gradient = np.zeros_like(params) # 結果格納用のリスト
    for i in range(len(params)):
        shifted = params.copy()
        shifted[i] += np.pi/2
        forward = cost_function(shifted)

        shifted[i] -= np.pi
        backward = cost_function(shifted)

        gradient[i] = 0.5 * (forward - backward)
    return gradient

勾配をもとに、共役勾配法(CG)で下ります。

from scipy.optimize import minimize
import time
np.random.seed(0)

var_init = np.random.uniform(low=-1, high=1, size=(2*3)) # one-dimensional array
hist_cost = []
var = var_init

count = 0
def cbf(Xi):
    global count
    global hist_cost
    cost_now = cost_function(Xi)
    hist_cost.append(cost_now)
    print('iter = '+str(count)+' | cost = '+str(cost_now))
    count += 1


t1 = time.time()
result = minimize(fun=cost_function, x0=var_init, method='CG', jac = my_grad, callback=cbf, options={"maxiter":200})
# 処理後の時刻
t2 = time.time() 
# 経過時間を表示
elapsed_time = t2-t1
print(f"経過時間：{elapsed_time}")

iter = 0 | cost = -0.46493436931195825
iter = 1 | cost = -0.6894640555873099
iter = 2 | cost = -0.9591867276137335
iter = 3 | cost = -0.9999742163624832
iter = 4 | cost = -0.9999999999999901
経過時間：1.575000286102295

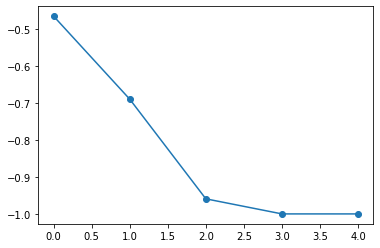
import matplotlib.pyplot as plt
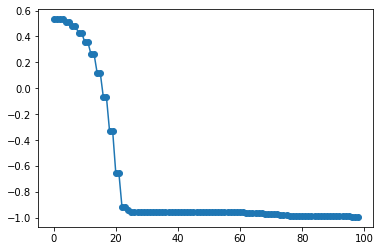
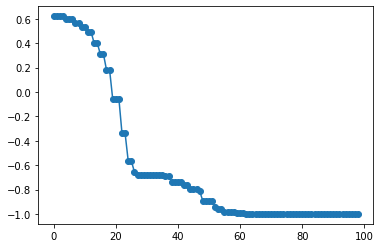
plt.plot(hist_cost,'o-')

あっという間に収束しました。

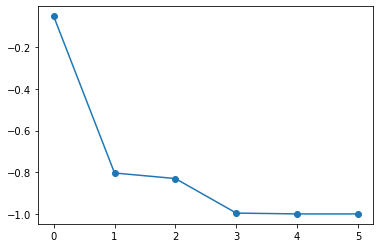
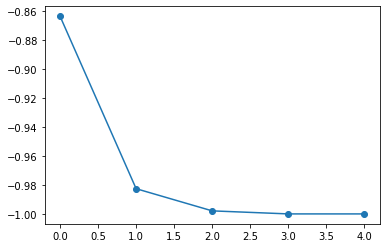
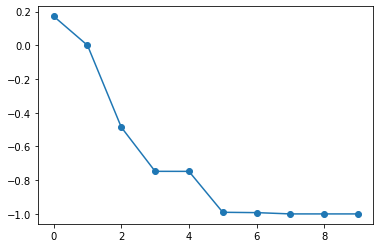
一応、初期値を変えて何度かやってみます。

10未満のiterationsで十分です。
やはり勾配降下は早いです。

まとめ

勾配降下は必須のツール？