周期グラフ上の離散時間量子ウォーク(Qiskit)

量子ウォーク

量子ウォークは、色々と応用が広い（らしい）量子問題です。
今回は簡単な例をqiskitで実装したサンプルコードを使って勉強します。
https://github.com/qiskit-community/qiskit-community-tutorials/blob/master/terra/qis_adv/quantum_walk.ipynb

なお上記サンプルコードにはtypoらしきものがあるので、修正していきます。

What is 量子ウォーク

8ノードの周期グラフ上の量子ウォークを考えます。

量子力学っぽい言い方をします。
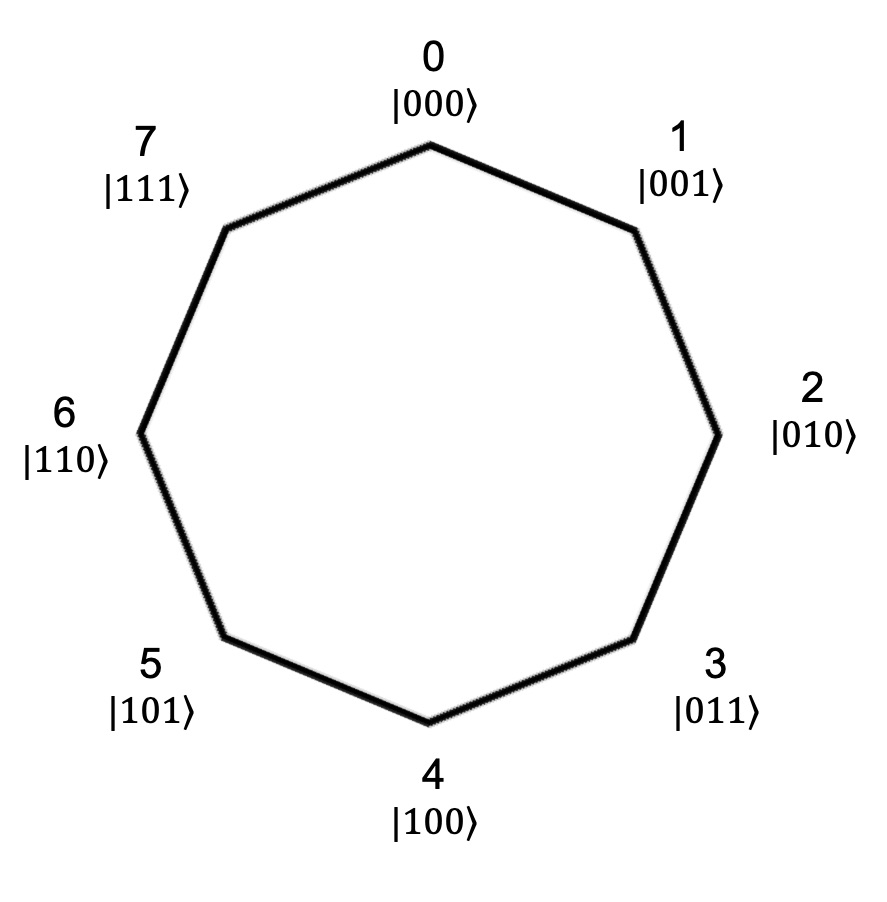
1量子の量子状態$|\psi \rangle$を考える。量子は8通りの位置のどこかに（一般には重ね合わせも許して）住んでいる。
つまり、{$|x=1\rangle, |x=2\rangle,...., |x=8\rangle$} を基底に持つ（位置基底）。¹
これを2進数表記すると、上記グラフのようになる。
また、量子はカイラリティと呼ばれる自由度{$|R\rangle, |L \rangle$}も持っている。
つまりこの1量子の量子状態の（カイラリティも含む）基底は　
{$|x=1\rangle \otimes |R \rangle, |x=1\rangle \otimes |L \rangle, |x=2\rangle \otimes |R \rangle...., |x=8\rangle \otimes |L \rangle$}
となる。

状態が定義できたので、次にこのグラフ上を”ウォーク”するシフト作用$S$を定義します。

• 量子状態が $|x=k\rangle \otimes |R \rangle$ であるとき(kは何でも良い）、このグラフ上を”右に”動く; $|x=k+1\rangle \otimes |R \rangle$
• 量子状態が $|x=k\rangle \otimes |L \rangle$ であるとき(kは何でも良い）、このグラフ上を”左に”動く; $|x=k-1\rangle \otimes |L \rangle$

もちろん、一般の量子状態は位置に関して重ね合わせされていますので、それらが同時に動くことになります。
”衝突”するのでは？と思いますが、そのとおりです。
線形性から、”衝突”した場合は、振幅が足し合わされることになります。干渉が起きるわけですね。

次に、コイン作用素$C$を定義します。
こちらは簡単で、

• 量子状態が $|x=k\rangle \otimes |W \rangle$ であるとき(k,Wは何でも良い）、カイラリティ次元に$H$を作用させる; $|x=k\rangle \otimes H|W \rangle$

となります。
位置はそのままで、カイラリティを変える、例えば$L$と$R$を入れ替えたり、$L$だけの状態を$R$と$L$の重ね合わせにしたりします。
$H$としては好きなユニタリ行列を考えましょう。何にしたかによって量子ウォークの挙動が変わります。
サンプルではアダマールゲートとしています。

量子ウォークでは、上記のコイン作用素$C$とシフト作用素$S$を1セットとして、繰り返します。
はじめに原点$|x=0 \rangle$に局在していたカイラリティ$|L \rangle$の状態が、ウォークと共に拡散していくこととなります。²

量子ビットと量子ゲートによる実装

上記問題を量子ビットで表現します。位置の量子ビットとしては3 bit、カイラリティとしては1 bitあればよいでしょう。³
コイン作用素は簡単で、カイラリティ次元の量子ビットにゲート$H$をかけてやればよいです。
シフト作用素は、カイラリティ次元の量子ビットを制御ビットとする”制御位置シフトゲート”をかけてやればよいです。
位置のシフトとは、カイラリティがRのときは位置(2進数表示)に1を足すことになりますので、加算器の応用で作れるでしょう。
例えば000が001へ行き、111が000へ行くようなゲートです。
カイラリティがLのときは減算器になるでしょう。
step = 2 のイメージ図です。

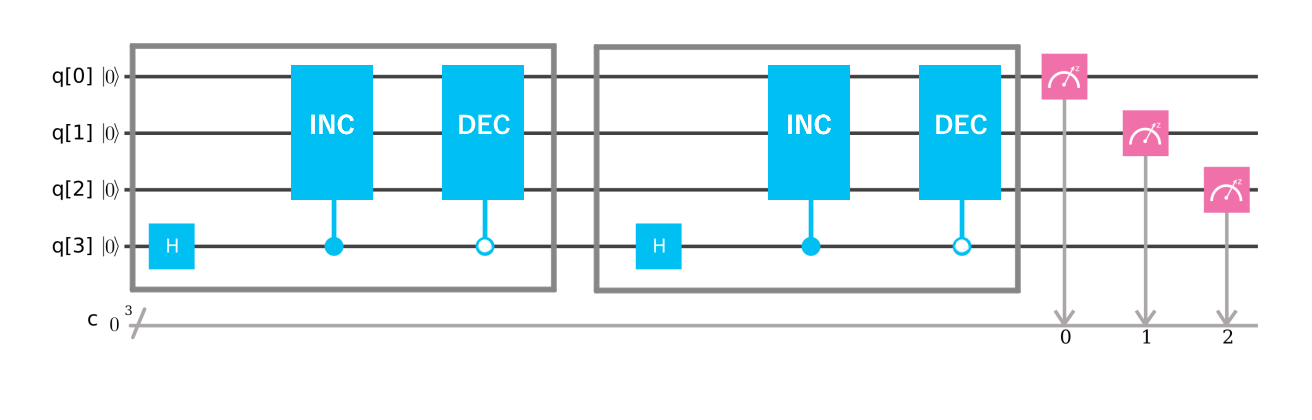
やってみますと、以下のようになります。
加算器・減算器を作るためにはマルチ制御ノットゲートCNXが必要なので、最初にそれを定義して、あとは組み合わせです。

import numpy as np
from qiskit import IBMQ, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import plot_histogram
from qiskit import Aer

n=3

def cnx(qc, *qubits):
    if len(qubits) >= 3:
        last = qubits[-1]
        # A matrix: (made up of a  and Y rotation, lemma4.3)
        qc.crz(np.pi/2, qubits[-2], qubits[-1])
        qc.cu3(np.pi/2, 0, 0, qubits[-2],qubits[-1])
        
        # Control not gate
        cnx(qc,*qubits[:-2],qubits[-1])
        
        # B matrix (pposite angle)
        qc.cu3(-np.pi/2, 0, 0, qubits[-2], qubits[-1])
        
        # Control
        cnx(qc,*qubits[:-2],qubits[-1])
        
        # C matrix (final rotation)
        qc.crz(-np.pi/2,qubits[-2],qubits[-1])
    elif len(qubits)==3:
        qc.ccx(*qubits)
    elif len(qubits)==2:
        qc.cx(*qubits)

def increment_gate(qwc, q, subnode):
  
  cnx(qwc, subnode, q[2], q[1], q[0])
  cnx(qwc, subnode, q[2], q[1])
  cnx(qwc, subnode, q[2])
  qwc.barrier()
  return qwc

def decrement_gate(qwc, q, subnode):
  
  qwc.x(subnode)
  qwc.x(q[2])
  qwc.x(q[1])
  cnx(qwc, subnode, q[2], q[1], q[0])
  qwc.x(q[1])
  cnx(qwc, subnode, q[2], q[1])
  qwc.x(q[2])
  cnx(qwc, subnode, q[2])
  qwc.x(subnode)
  return qwc
  
def ibmsim(circ):
  ibmqBE = Aer.get_backend('qasm_simulator')
  return execute(circ,ibmqBE, shots=1000).result().get_counts(circ)  

qnodes = QuantumRegister(n,'qc')
qsubnodes = QuantumRegister(1,'qanc')
#csubnodes = ClassicalRegister(1,'canc')
cnodes = ClassicalRegister(n,'cr')

qwc = QuantumCircuit(qnodes, qsubnodes, cnodes)


def runQWC(qwc, times):
    for i in range(times):
        qwc.h(qsubnodes)
        increment_gate(qwc, qnodes, qsubnodes)
        decrement_gate(qwc,qnodes,qsubnodes)
        qwc.barrier()
        qwc.measure(qnodes, cnodes)

    return qwc

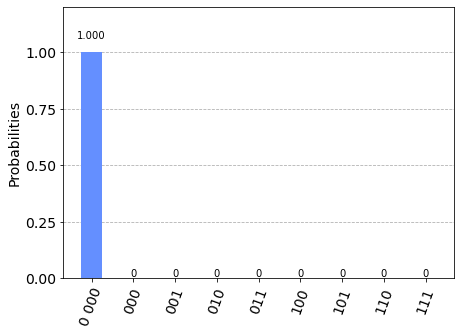
できました。初期状態 step = 0 をみてみます。

import matplotlib as mpl

# zero-padding
def zero_padding_counts(counts):
    nqubits = n
    for i in range (2**nqubits):
        counts.setdefault(format(i, '0'+str(nqubits)+'b'),0)

step = 0
qwc = QuantumCircuit(qnodes, qsubnodes, cnodes, csubnodes) # initialize
qwc = runQWC(qwc, step)
result = ibmsim(qwc)
zero_padding_counts(result)
plot_histogram(result)

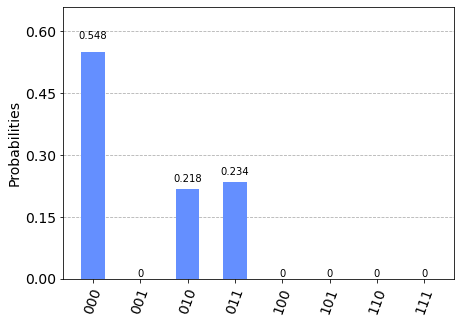
位置(3量子ビット)を測定した結果、初期状態では原点$|x = 0 \rangle = |000 \rangle$ にいます。

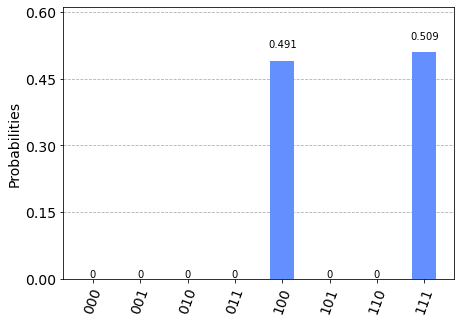
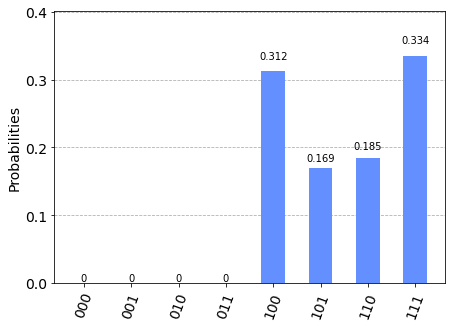
次にstep = 1 です。

注意点として、bitの桁は上から下に向かって読んでください。qiskitの仕様です。
001と111に居る、となっていますね。
原点にいた量子に対して、$H$ゲートでカイラリティがRとLの重ね合わせになった後、シフト作用素をかけますので、50%/50%の重みで000と111へいくわけですね。

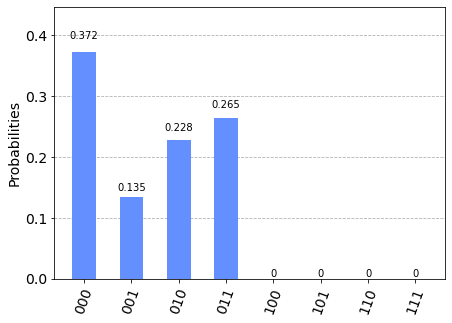
次にstep = 2です。

もうよくわからないのですが、おそらく000のところで同位相で”衝突”しています。
010と011は、もともと空席だったので、そのまま着地していますね。

step = 3です。

step = 4です。

step = 5です。

実はstep=3の状態に戻ってきています。
これ以上繰り返しても、周期的に繰り返されます。
循環グラフ上で「定在波ができた」と考えてよいかと思います。

まとめ

循環グラフ上の量子ウォークを実装した。
これで何ができるのかはわからないので、もっと勉強します。

1. 位置基底で表示した時の振幅値を、波動関数といいます。大学で少し量子力学を触った方は、波動関数が量子状態と教わったかもしれません。正確には、量子状態を”位置”という基底で展開した時の姿が波動関数なのであって、波動関数を基礎に置きすぎることはよくありません。 ↩

2. もしコイン作用素がない場合はどうなるでしょう？　量子は左方向へ動き続けるため、位置が局在したままぐるぐる回ることになりますね。もしシフト作用素がない場合はどうなるでしょう？量子の位置は原点から動かないまま、カイラリティだけが変わることになります。 ↩

3. (念の為)位置は8量子ビットではありません。あくまで、1量子の位置状態が8通りあるだけで、8量子ビットが相互作用する問題を考えているわけでは有りません。また、Rが$|1 \rangle$でLが$|0 \rangle$となるように定義します。 ↩