Go to Qiita Advent Calendar 2024 Top
LoginSignup
2
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@notdeclared(NeeeeT)

競プロのTLE解法を救いたい with FPGA ~HLS編~

Last updated at Posted at 2021-03-09

#はじめに
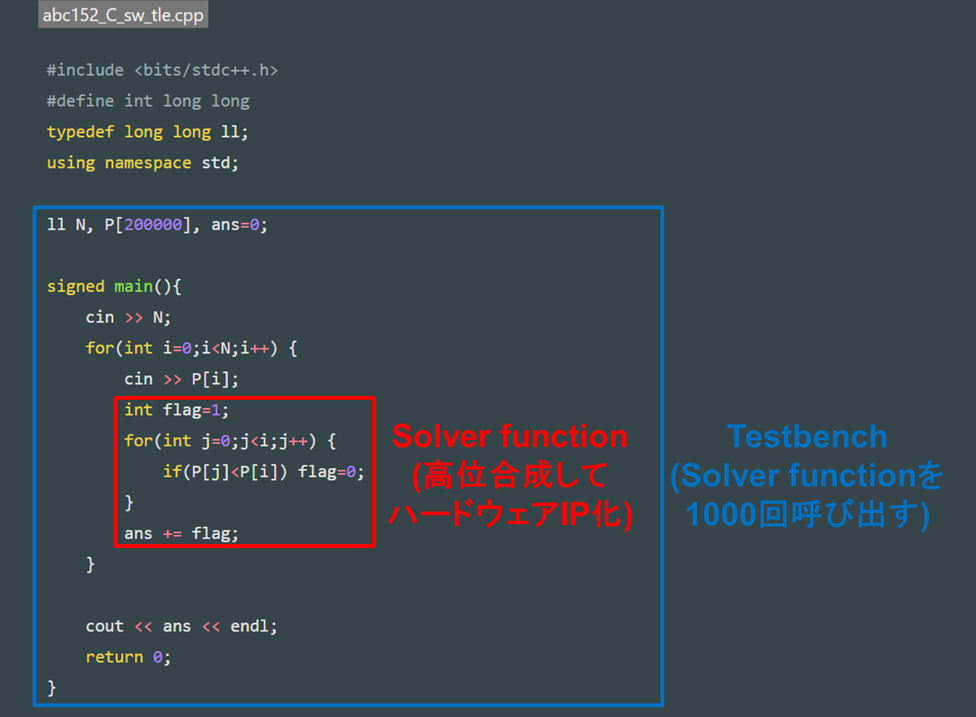
この記事は、ソフトウェア技術者(競プロ勢含む)へのハードウェアアクセラレータ開発への導入とハードウェア技術者へのXilinx FPGA (Field Programmable Gate Array) を用いたアーキテクチャのチューニング手法の提示を目的として作成しました。この記事では、atcoder beginners contest 152のC問題でTLE (Time Limit Exceeded) したCプログラムをHLS (High Level Synthesis) で並列化、パイプライン化し、Xilinx FPGAで動作するatcoder beginners contest 152のC問題のソルバーIP (Intellectual Property) を作っていきます。すでに、Verilog HDLを用いた記事はありますが、今回はFPGAを使うのが初めてのソフトウェアエンジニアの方にも読みやすいように全ての開発をC++言語縛りとし、HLSでチューニングを行い、ソルバーIPを作成し、ZYNQと組み合わせて、実際に制限時間内に収まるのか実機検証していきます。

今回はHLS編として、前回の記事で説明したTLE解法を記述したC++プログラムをベースとしてVivado HLSを使ってチューニングを行い、Xilinx FPGAで動作する最適化したatcoder beginners contest 152のC問題のソルバーIPを作っていきます。

Flow_2.png

#用語の説明
##HLS (High Level Synthesis : 高位合成)
HLSとは、C/C++言語から論理回路を生成する設計手法。HDLでは必要となるクロックごとの処理を記述する必要があるのに対し、HLSでは、クロックを意識する必要がありません。また、C/C++言語で処理を記述することができるため、同等の処理をHDLで記述するより少ない記述量ですませることができます。これらのメリットから、HLSを使うことによりソフトウェア開発に近い感覚で設計を行うことができ、開発期間を短縮することができます。

##HDL (Hardware Description Language : ハードウェア記述言語)
HDLとは、論理回路設計のためのプログラミング言語。HDLではクロックごとの処理を記述する必要があります。HDLは抽象度の低いプログラミング言語であるため、処理に対し記述量が多くなってしまいます。

#ソフトウェアの役割
##Vivado
・HDLやブロックデザインを使ったハードウェア設計
・FPGAに実装する際に必要となるピン配置などの制約を生成
・FPGAのコンフィグレーションに必要となるビットストリームを生成

##Vivado HLS
・C/C++言語で記述された処理をHDLに変換
・C/C++言語で記述されたテストベンチと組み合わせたシミュレーション
・IPとしてVivadoにエクスポート

##Vivado SDK
・ZYNQ内蔵のARM CPUで動作するソフトウェア設計
・Terminal等を用いた動作検証

#HLSを使ったソルバーIP設計 (1)
##TLE解法をIP化してみる
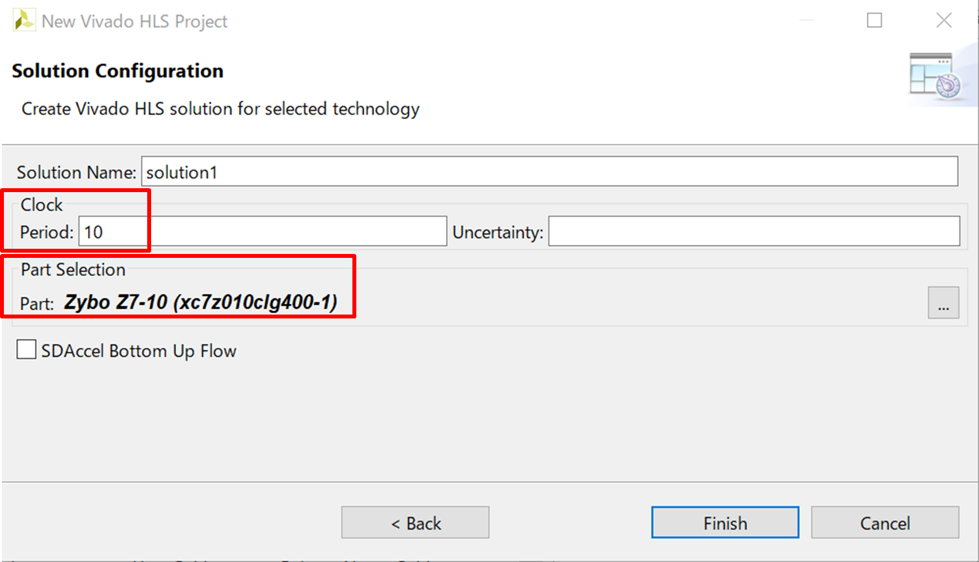
ここでは、前回の記事で説明したTLE解法を記述したC++プログラムを高位合成していきます。HLSでは、処理をC/C++言語で記述し、インターフェースやハードウェア構成等をプラグマ (指示子) で与えていきます。今回はインターフェースのみ指定し、ハードウェア構成を最適化しないままIP化していきます。最適化の効果を分かりやすくするため、データの入力サイズSIZEを200000から1000に変更しました。Clock→Periodを10nsec、PartSelection→PartをZYBO (Z7-10) に設定してプロジェクトを作成します。ソルバーIPとテストベンチのC++プログラムを以下に記載します。

ProjectSettings.png

HLS_1.png

abc152_C_zybo_1.cpp
// Define input size as 1000.
#define SIZE 1000

// Define my "solver" function.
void solver(volatile int *P, int i, int *ans) {
#pragma HLS INTERFACE m_axi port=P depth=1000 offset=slave bundle=array // Set interface of port "P" as axi interface and data size as 1000.
#pragma HLS INTERFACE s_axilite port=i // Set interface of port "i" as axilite interface.
#pragma HLS INTERFACE s_axilite port=ans // Set interface of port "ans" as axilite interface.
#pragma HLS INTERFACE s_axilite port=return // Control my "solver" IP using axilite.

	int flag=1;
	loop1: for(int j=0;j<SIZE;j++) {
		if(P[j]<P[i]) flag=0;
	}
	*ans += flag;
}
abc152_C_zybo_1_tb.cpp
#include <iostream>

// Define input size as 1000.
#define SIZE 1000

// declare my "solver" function
void solver(volatile int *P, int i, int *ans);

int main() {
	int P[SIZE]; // Variable "P" is an array for input of my "solver" function.
	int I[SIZE]; // Variable "I" is an array to keep sample cases.
	int ans=0; // Variable "ans" is the result of this testbench.

	// Initialize array "P".
	for(int i=0;i<SIZE;i++) {
		P[i] = 200001;
	}

	// Initialize array "I".
	for(int i=0;i<SIZE;i++) {
		I[i] = 200001;
	}
	/* sample case 1, ans : 3
	I[0] = 4;
	I[1] = 2;
	I[2] = 5;
	I[3] = 1;
	I[4] = 3;
	*/
	/* sample case 2, ans : 4
	I[0] = 4;
	I[1] = 3;
	I[2] = 2;
	I[3] = 1;
	*/
	/* sample case 3, ans : 1
	I[0] = 1;
	I[1] = 2;
	I[2] = 3;
	I[3] = 4;
	I[4] = 5;
	I[5] = 6;
	*/
	/* sample case 4 , ans : 4*/
	I[0] = 5;
	I[1] = 7;
	I[2] = 4;
	I[3] = 2;
	I[4] = 6;
	I[5] = 8;
	I[6] = 1;
	I[7] = 3;

	/* sample case 5, ans : 1
	I[0] = 1;
	*/

	// Repeat a SIZE(1000) times, substituting a sample case array for an input array of my "solver" function and calling my "solver" function.
	for(int i=0;i<SIZE;i++) {
		P[i] = I[i];
		solver(&P[0], i, &ans);
	}

	// Display the result of this testbench.
	std::cout << "ans : " << ans << std::endl;

	return 0;
}

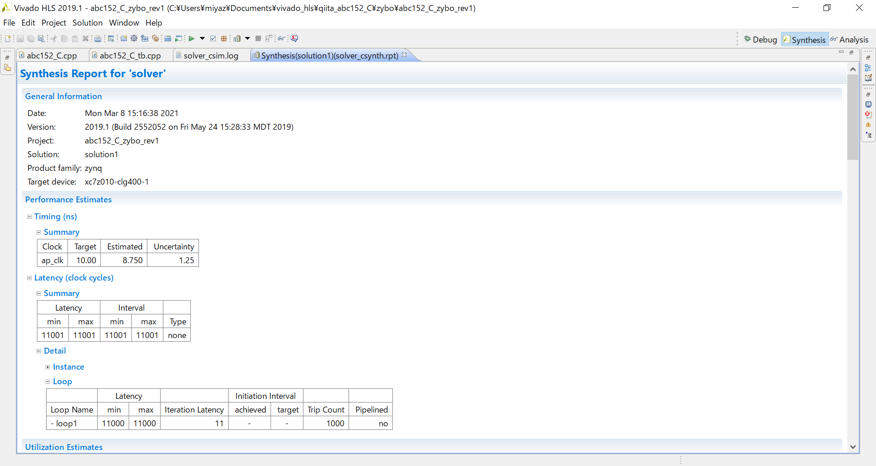
高位合成した結果は以下のようになりました。

HLS_1_synth.png

Loop1のIteration Latencyが11となっています。これは、ソルバーIP内のLoop1内の1回の処理に11クロック分の時間がかかることを意味します。よって、ソルバーIPの1回あたりの実行時間を概算すると、データの入力サイズをSIZEとした時に、SIZE回だけ処理を行うため11SIZE回程度のクロック分の時間がかかることになります。そして、テストベンチからソルバーIPをSIZE回呼び出すため、全部で11SIZE2回程度のクロック分の時間を要します。今回は、クロックを100MHzに設定しているため、データの入力サイズをSIZEとした時に、全体の処理時間TALLは以下の式で表すことができます。

T_{ALL} = 11SIZE^{2}/10^{8} (sec)

よって、データの入力サイズSIZEを1000、200000とした時には、それぞれ0.11sec、4.4×103sec程度となり、入力サイズSIZEが200000の時には、1時間以上の時間を要することが分かります。

#HLSを使ったソルバーIP設計 (2)
##ソルバーIPの高速化
ソルバーIPを高速化するにあたり、重要な点を3つにまとめます。

1. DDRアクセス回数の削減
2. UNROLLプラグマを用いた処理の並列化
3. ARRAY_PARTITIONプラグマを用いたメモリの広帯域化

これらの3つの要素を、ソルバーIPに対して適用していきたいと思います。まず、現状の構成ではテストベンチから入力データサイズSIZEと等しい回数だけソルバーIPが呼び出され、AXIインターフェースで配列Pが、AXI LITEインターフェースでiとansが転送されています。毎回、PS側にあるDDRとPLの間でデータ転送をするのは、効率が悪いので、ソルバーIPの呼び出しを1回として、データ転送にかかる時間を大幅に削減します。次に、現状の構成ではソルバーIPを呼び出すと、入力データサイズSIZEと等しい回数だけPi ＞ Pjの結果に応じて、フラグを下げる処理を逐次的に行っていましたが、UNROLLプラグマを利用して、並列的に処理を行います。最後に、FPGA上にもBRAMというメモリが存在しますが、現状の構成では、処理を並列化してもBRAMからデータを逐次的に読み出し/書き込みを行っているため、メモリアクセスがボトルネックとなってしまいますが、ARRAY_PARTITIONプラグマを利用して、BRAMからデータを並列的に読み出し/書き込みを行います。

コードの変更点を簡単にまとめます。

・PSからソルバーIPをデータの入力サイズSIZEと等しい回数だけ呼び出すのではなく、ソルバーのラッパーIPを生成し、ラッパーIPからソルバーをデータの入力サイズSIZEと同じだけ呼び出すことにします。これにより、PSからソルバーのラッパーIPへの1回だけのアクセスで済みますが、ソルバーを呼び出すごとに、PL内部の配列Pを更新していく必要があるため、新しい静的配列Pが必要となる。(BRAMの使用率が高くなる)
・配列P[SIZE]をP[TIMES][PSIZE]と2次元化しました。PSIZEは並列度を表しており、配列Pの2次元目はすべての処理が並列に行われています。今回は、SIZEとPSIZEをそれぞれ1000、50であり、1000回の処理を50並列で行うため、Loop4のループ回数TIMESは20となります。
・その他にも、intからboolに変更したり、多ビット演算をビット演算で置き換えることによって、論理回路の高速化と省面積化を行っています。

Clock→Periodを10nsec、PartSelection→PartをZYBO (Z7-10) に設定してプロジェクトを作成します。ソルバーIPとテストベンチのC++プログラムを以下に記載します。

abc152_C_zybo_2.cpp
// Define loop times as 20.
#define TIMES 20
// Define the parallel degree as 50.
#define PSIZE 50

// Define my "solver" function.
void solver(int i, int pi, int *ans) {
#pragma HLS inline
	// "P" is a temporary array that is initialized as 200001s.
	static int P[TIMES][PSIZE] = {{200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}, {200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001, 200001}};

#pragma HLS ARRAY_PARTITION variable=P complete dim=2 // P[j][k] (0≦k≦PSIZE-1) can be accessed at a time.

	int tmp1 = i/PSIZE; // Calculate the index of dim 1 of 2D array "P".
	int tmp2 = i%PSIZE; // Calculate the index of dim 2 of 2D array "P".

	P[tmp1][tmp2] = pi; // Substitute variable "pi" for a temporary array "P".

	bool tmp = 0; // Variable "tmp" acts as flag, initialized as 0.
	loop3: for(int j=0;j<TIMES;j++) {
		loop4: for(int k=0;k<PSIZE;k++) {
#pragma HLS UNROLL // PSIZE calculations of Loop4 are processed in parallel.
			tmp |= (P[j][k] < pi); // If P[j][k] is less than pi, variable "tmp" is set as 0.
		}
	}
	*ans += !tmp; // If tmp is 0, ans is increased by 1.
}

// Define new wrapper function that calls my "solver" function N times.
int solver_wrapper(volatile int *A) {
#pragma HLS INTERFACE s_axilite port=return // Control my "solver" IP using axilite.
#pragma HLS INTERFACE m_axi port=A depth=1000 offset=slave bundle=array // Set interface of port "P" as axi interface and data size as 1000.
	int ans=0; // Variable "ans" is the result of this "solver_wrapper" function.

	// Repeat a TIMES(20)*PSIZE(50) times, calling my "solver" function.
	loop1: for(int i=0;i<TIMES*PSIZE;i++) {
		solver(i, A[i], &ans);
	}
	return ans;
}
abc152_C_zybo_2_tb.cpp
#include <iostream>

// Define loop times as 20.
#define TIMES 20
// Define the parallel degree as 50.
#define PSIZE 50

// Declare my "solver_wrapper" function.
int solver_wrapper(volatile int *A);

int main() {
	int I[TIMES*PSIZE]; // Variable "I" is an array to keep sample cases.
	int ans=0; // Variable "ans" is the result of this testbench.

	// Initialize array "I".
	for(int i=0;i<TIMES*PSIZE;i++) {
		I[i] = 200001;
	}
	/* sample case 1, ans : 3
	I[0] = 4;
	I[1] = 2;
	I[2] = 5;
	I[3] = 1;
	I[4] = 3;
	*/
	/* sample case 2, ans : 4
	I[0] = 4;
	I[1] = 3;
	I[2] = 2;
	I[3] = 1;
	*/
	/* sample case 3, ans : 1
	I[0] = 1;
	I[1] = 2;
	I[2] = 3;
	I[3] = 4;
	I[4] = 5;
	I[5] = 6;
	*/
	/* sample case 4, ans : 4 */
	I[0] = 5;
	I[1] = 7;
	I[2] = 4;
	I[3] = 2;
	I[4] = 6;
	I[5] = 8;
	I[6] = 1;
	I[7] = 3;

	/* sample case 5, ans : 1
	I[0] = 1;
	*/
	
	// Display the result of this testbench.
	std::cout << "ans : " << solver_wrapper(I) << std::endl;

	return 0;
}

高位合成した結果は以下のようになりました。

HLS_2_synth.png

Loop1のIteration Latencyが43となっています。これは、ソルバーのラッパーIP内のLoop1内の1回の処理に43クロック分の時間がかかることを意味します。よって、ソルバーの1回あたりの実行時間が43クロック分の時間であることを意味します。高速化する前のソルバーの1回あたりの実行時間は11000クロック分の時間だったので、250倍以上の高速化となっていることが分かります。並列度は50に設定しましたが、並列度だけでなくビット数、演算子、メモリアクセスを変更することによってさらに高速化を行うことができたことが分かります。

#データサイズを1000から200000に変更すると…
ここまでは、データの入力サイズSIZEを1000として、ソルバーIPを設計してきました。あとは、データの入力サイズSIZEを200000として、高位合成をするだけで機能的には正しく動作するものが作れるでしょう。では、データの入力サイズSIZEを200000として、高位合成したらどのような合成結果が得られるでしょうか。結果から言うと、BRAMの使用率が100%を大幅に超えます。今回の問題設定では、メモリ制限は1024MBとなっているのに対し、ZYBO (Z7-10) のBRAM容量MCは、0.26MBしかないため、時間制限だけでなく、メモリ制限も非常に厳しい制約となっていることが分かります。

MC = 120(個数)×18k(b)/8M(b/MB) = 120×18×1024/(8×1024×1024) = 0.26 (MB)

データの入力サイズSIZEを200000とした時の、static intで宣言している配列Pに必要となるBRAMの個数Nを計算してみると、BRAMを最大効率で使用しても348個必要となってしまい、ZYBO (Z7-10) が持つ120個のBRAMには収まりません。

N = 200000×32(b)/18k(b) = 200000×32(b)/(18×1024) = 347.2

また、BRAMを並列にアクセスするためにBRAMを細かく分割して使用しているため、BRAMを最大効率で使用することはできません。例えば、並列度PSIZEを50とした時は、50の倍数だけBRAMが必要となってしまうため、400個以上のBRAMが必要になると考えられます。内部のメモリを小さくしてしまうと、PLからPS側のDDRへのアクセス回数が増えてしまい、時間制限である2secを満たすことができません。 (実際にいろいろ試してみましたが、2secを満たすことはできませんでした。) このあたりが、ZYBO (Z7-10) のリソースと実行速度のトレードオフになると私は思っています。 (合成結果のリソースの使用率がアンバランスであり、上手にバランスをとればメモリ制限と時間制限を同時に満たすことができるかもしれないので、断定はできませんが…)

#結局は…
さらに最適化を行い、ZYBO (Z7-10) でメモリ制限と時間制限を同時に満たすことができる可能性はありますが、高度な技術と長い開発時間を要する上に、できる保証もありません。そこで、解決策の一例として、私がとった解決策を提示したいと思います。432個のBRAMを持つUltra96 v2 Evaluation Boardを購入しました。いろいろ試してみましたが、結局、お金が全て解決してくれました。世知辛い…

#HLSを使ったソルバーIP設計 (3)
参考までに、Ultra96 v2 Evaluation Boardを使うと、高位合成の結果はどうなるのかを検証していきます。コードの変更点を簡単にまとめます。

・配列P[SIZE]をP[TIMES][PSIZE]と2次元化しました。PSIZEは並列度を表しており、配列Pの2次元目はすべての処理が並列に行われています。今回は、SIZEとPSIZEをそれぞれ200000、1000であり、200000回の処理を1000並列で行うため、Loop4のループ回数TIMESは200となります。
・ARRAY_PARTITIONプラグマをcomplete dim=2からcyclic factor=200 dim=2へと変更しました。complete (1000並列) では、1000個のBRAM必要となり、BRAMが不足してしまったため、200並列でBRAMアクセスをしたところ400個のBRAMで収まりました。

Clock→Periodを10nsec、PartSelection→PartをUltra96v2 Evaluation Platformに設定してプロジェクトを作成します。ソルバーIPとテストベンチのC++プログラムを以下に記載します。(abc152_C_ultra_1.cppの配列Pを全て200001で初期化して使ってください。要素数が多く記事のロード時間が長くなってしまったので、このような構成に変更しました。配列Pの初期化用のPythonスクリプトも記載しておきます。)

ProjectSettings_ultra.png

abc152_C_ultra_1.cpp
// Define loop times as 200.
#define TIMES 200
// Define the parallel degree as 1000.
#define PSIZE 1000

// Define my "solver" function.
void solver(int i, int pi, int *ans) {
#pragma HLS inline
	// "P" is a temporary array that is initialized as 200001s.
	static int P[TIMES][PSIZE] = {/*全て200001で初期化*/};

// P[j][k] (0≦k≦199) can be accessed at a time.
#pragma HLS ARRAY_PARTITION variable=P cyclic factor=200 dim=2 // 400 BRAM18K
// #pragma HLS ARRAY_PARTITION variable=P cyclic factor=250 dim=2 // 500 BRAM18K
// #pragma HLS ARRAY_PARTITION variable=P cyclic factor=500 dim=2 // 1000 BRAM18K

	int tmp1 = i/PSIZE; // Calculate the index of dim 1 of 2D array "P".
	int tmp2 = i%PSIZE; // Calculate the index of dim 2 of 2D array "P".

	P[tmp1][tmp2] = pi; // Substitute variable "pi" for a temporary array "P".

	bool tmp = 0; // Variable "tmp" acts as flag, initialized as 0.
	loop3: for(int j=0;j<TIMES;j++) {
		loop4: for(int k=0;k<PSIZE;k++) {
#pragma HLS UNROLL // PSIZE calculations of Loop4 are processed in parallel.
			tmp |= (P[j][k] < pi); // If P[j][k] is less than pi, variable "tmp" is set as 0.
		}
	}
	*ans += !tmp; // If tmp is 0, ans is increased by 1.
}

// Define new wrapper function that calls my "solver" function TIMES*PSIZE times.
int solver_wrapper(volatile int *A) {
#pragma HLS INTERFACE s_axilite port=return // Control my "solver" IP using axilite.
#pragma HLS INTERFACE m_axi port=A depth=200000 offset=slave bundle=array // Set interface of port "P" as axi interface and data size as 200000.
	int ans=0; // Variable "ans" is the result of this "solver_wrapper" function.

// Repeat a TIMES(200)*PSIZE(1000) times, calling my "solver" function.
	loop1: for(int i=0;i<TIMES*PSIZE;i++) {
		solver(i, A[i], &ans);
	}
	return ans;
}
abc152_C_ultra_1_tb.cpp
#include <iostream>

// Define loop times as 200.
#define TIMES 200
// Define the parallel degree as 1000.
#define PSIZE 1000

// Declare my "solver_wrapper" function.
int solver_wrapper(volatile int *A);

int main() {
	int I[TIMES*PSIZE]; // Variable "I" is an array to keep sample cases.
	int ans=0; // Variable "ans" is the result of this testbench.

	// Initialize array "I".
	for(int i=0;i<TIMES*PSIZE;i++) {
		I[i] = 200001;
	}
	/* sample case 1, ans : 3
	I[0] = 4;
	I[1] = 2;
	I[2] = 5;
	I[3] = 1;
	I[4] = 3;
	*/
	/* sample case 2, ans : 4
	I[0] = 4;
	I[1] = 3;
	I[2] = 2;
	I[3] = 1;
	*/
	/* sample case 3, ans : 1
	I[0] = 1;
	I[1] = 2;
	I[2] = 3;
	I[3] = 4;
	I[4] = 5;
	I[5] = 6;
	*/
	/* sample case 4, ans : 4 */
	I[0] = 5;
	I[1] = 7;
	I[2] = 4;
	I[3] = 2;
	I[4] = 6;
	I[5] = 8;
	I[6] = 1;
	I[7] = 3;

	/* sample case 5, ans : 1
	I[0] = 1;
	*/
	
	// Display the result of this testbench.
	std::cout << "ans : " << solver_wrapper(I) << std::endl;

	return 0;
}
static_initialize.ipynb
TIMES = 200
PSIZE = 1000
str_tmp = 'static int P[TIMES][PSIZE] = {'
for i in range(TIMES):
    str_tmp += '{200001'
    for j in range(PSIZE-1):
        str_tmp += ', 200001'
    str_tmp += '}, '
    
str_tmp = str_tmp.rstrip(", ")
str_tmp += '};'
print(str_tmp)

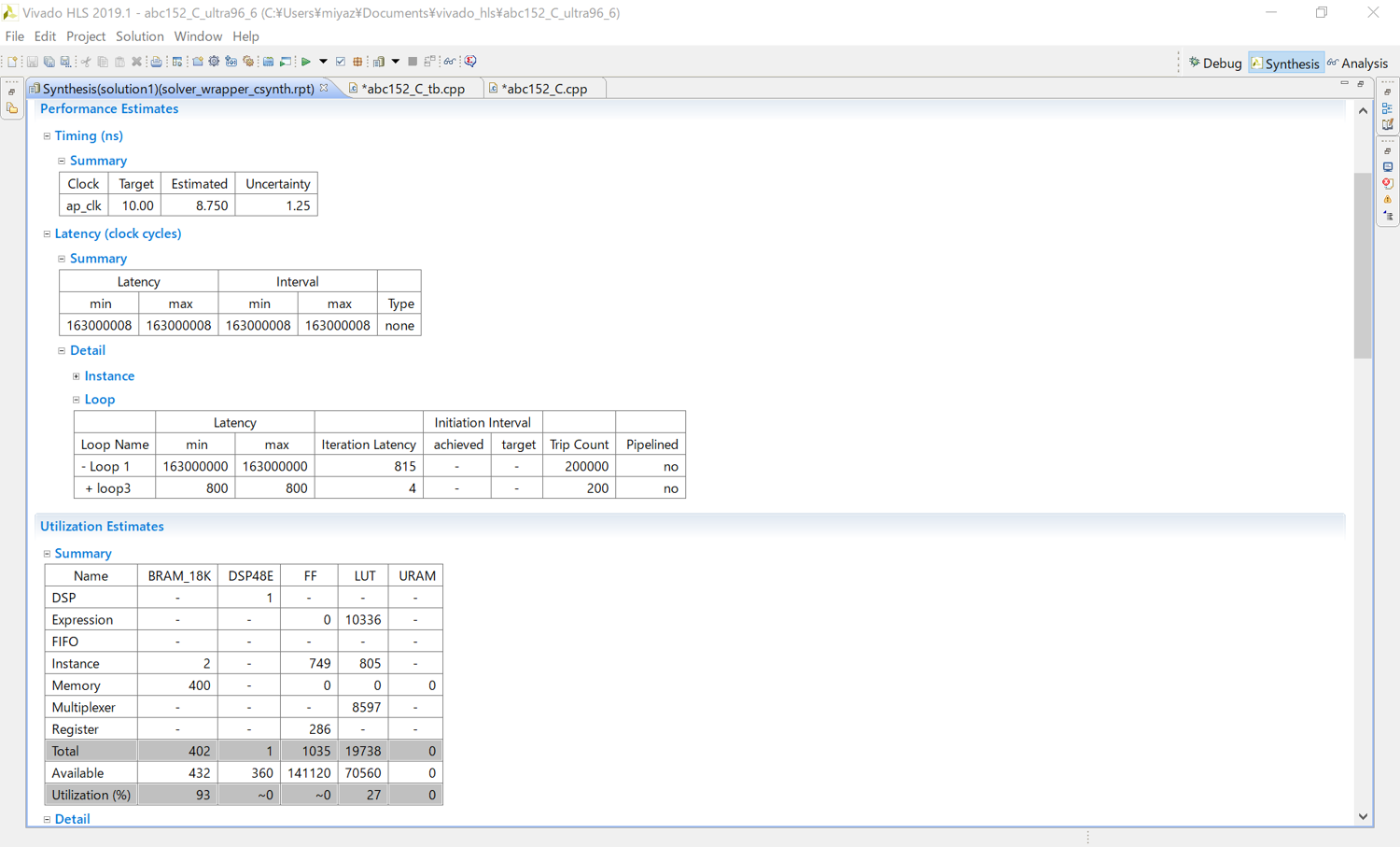
高位合成した結果は以下のようになりました。

HLS_3_synth.png

BRAMの使用率は93%となり、ギリギリ収まっていることが分かります。Latencyは163000008となっています。これは、ソルバーのラッパーIPの処理に163000008回のクロック分の時間がかかることを意味します。今回は、クロックを100MHzに設定しているため、処理時間は1.63secとなります。時間制限である2secの実行時間もギリギリ満たしていることが分かります。

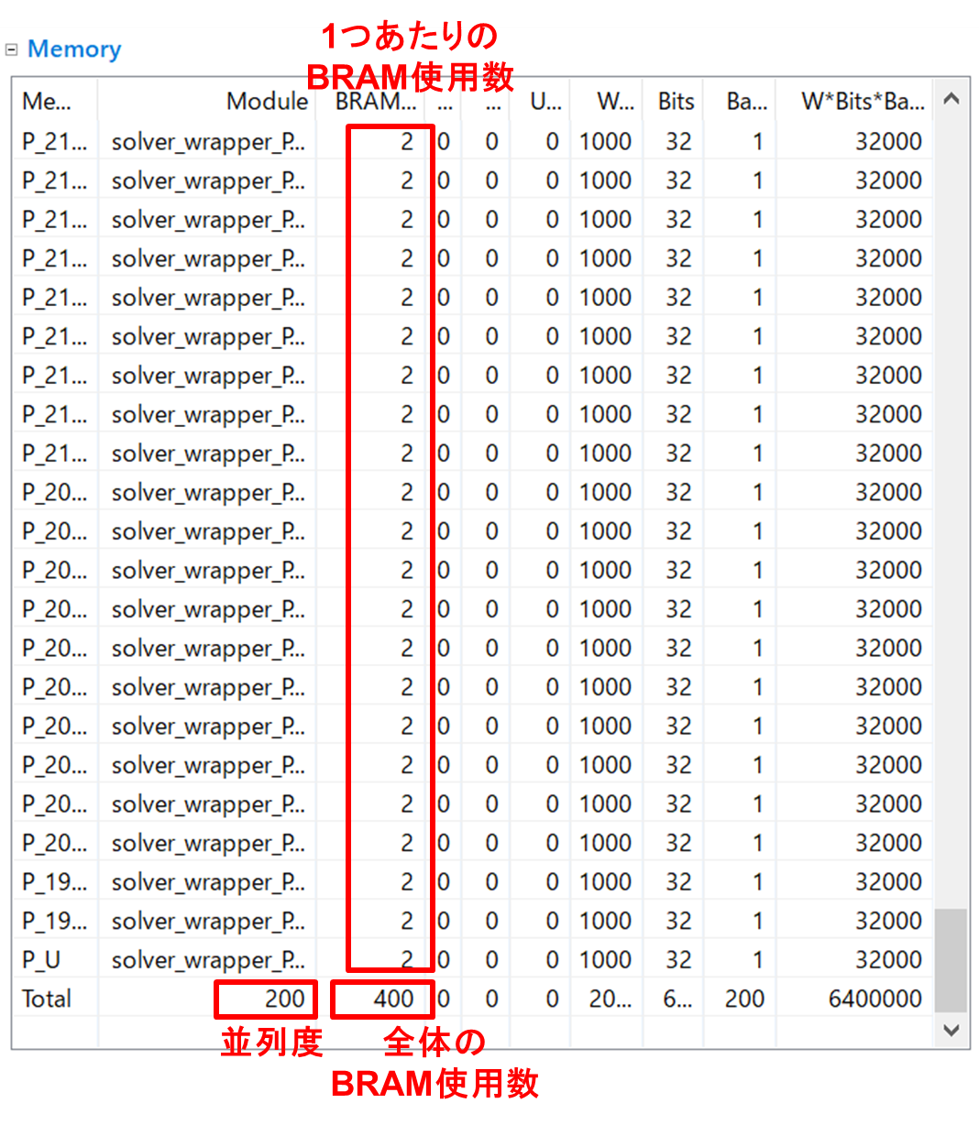
もう少し詳細な合成結果を見てみると、BRAMの使用数に関しては、並列度200で並列化されており、並列化されたそれぞれの配列が2つのBRAMで収まっているため、400個のBRAMで収まっています。並列度1000で並列化すると、並列化されたそれぞれの配列のデータ数が1/5になるため、1つのBRAMで収まりますが、全体で1000個のBRAMが必要になるため、BRAMが不足することが分かります。

HLS_3_synth_BRAM.png

実行時間に関しては、並列度1000で並列化されており、1000回の計算を4クロックサイクルで全て計算することができます。あとは、この1000回の計算を200回繰り返し、さらに200000回繰り返すと163000008クロックサイクルのLatencyとなることが分かります

HLS_3_synth_TIME.png

#おわりに
今回の記事ではHLS編ということで、UNROLLプラグマを用いた処理の並列化とARRAY_PARTITIONプラグマを用いたメモリの広帯域化を適用して、atcoder beginners contest 152のC問題のソルバーの高速化を行い、時間制限を満たしました。そして、ZYBO (Z7-10) からUltra96 v2 Evaluation Boardに変更することでリソースの制約を満たしました。次の記事で、VIvadoを使って、今回作成したソルバーIPとZYNQと組み合わせてハードウェアを作成し、Xilinx SDKを使って、ARMプロセッサ上で動作するプログラムを作成し、制限時間内に収まるのか実機検証していきます。

"TLE解法を救いたい"

2
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?