はじめに
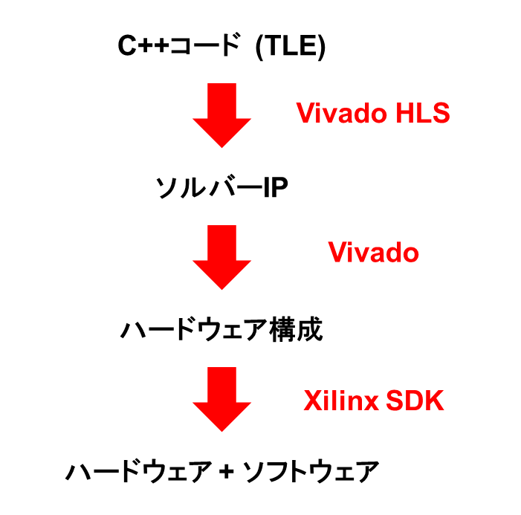
この記事は、ソフトウェア技術者(競プロ勢含む)へのハードウェアアクセラレータ開発への導入とハードウェア技術者へのXilinx FPGA (Field Programmable Gate Array) を用いたアーキテクチャのチューニング手法の提示を目的として作成しました。この記事では、atcoder beginners contest 152のC問題でTLE (Time Limit Exceeded) したC++プログラムをHLS (High Level Synthesis) で並列化、パイプライン化し、Xilinx FPGAで動作するatcoder beginners contest 152のC問題のソルバーIP (Intellectual Property) を作っていきます。すでに、Verilog HDLを用いた記事はありますが、今回はFPGAを使うのが初めてのソフトウェアエンジニアの方にも読みやすいように全ての開発をC++言語縛りとし、HLSでチューニングを行い、ソルバーIPを作成し、ZYNQと組み合わせて、実際に制限時間内に収まるのか実機検証していきます。
今回は導入編として、atcoder beginners contest 152のC問題の問題概要を説明した後に、よくあるTLE解法とAtCoderで推奨されているAC (Accepted) 解法の比較を行いたいと思います。
速度性能向上へのアプローチ
何かのアプリケーションを作ろうとした時には、必ず仕様というものが存在します。速度性能の仕様を満たせない場合はどうなるでしょうか。
自動運転のアプリケーションの場合は、制御システムの応答時間が長くなると治安が悪くなります。AtCoderのコンテストに出ていた場合は、TLEでペナルティを受け、レートが溶けます。AtCoderのペナルティはUnratedに一縷の望みを託しますが、交通事故にUnratedはありませんので避けるべきでしょう。このように、アプリケーションの制御システムの応答時間を短縮する必要がある場合は日常的に起こります。そこで、アプリケーションの制御システムの応答時間を決める要素はいくつか考えられますが、今回はアプリケーションに必要となる計算にかかる処理時間を短縮することにより応答時間の短縮することを考えていきます。
1. 計算量の少ないアルゴリズムを選択 (ソフトウェアレベル)
2. スループットの高いアーキテクチャを作成 (ハードウェアレベル)
1つ目は競技プログラミングで多く用いられるアプローチです。アプリケーション実装に必要な作業は、CPU上で動作するプログラムを作成することであるので、非常に汎用性の高いアプローチと言えると思います。こちらのアプローチに関しては、書籍やAtCoder社の解説PDFで分かりやすく解説してありますので、そちらを参照してください。
2つ目のアプローチは、必要となる計算に最適なアーキテクチャを生成する必要があります。計算に必要となるデータの依存性等を考慮し、並列構成やパイプライン構成のアーキテクチャを作成していきます。アプリケーションの実装は多くの場合、FPGAを使います。Xilinx社のZYBOというFPGAは、PS (Processing System) というCPUとPL (Programmable Logic) というHDL (Hardware Description Language) を使って書き換え可能なハードウェアが入っており、合わせてSoC (System On Chip) と呼ばれたりします。一般的なFPGAを用いたアプリケーション実装に必要な作業としては、HDLを用いてPLを書き換え、PSと接続し、SDK (Software Development Kit) を用いてPSのARMプロセッサ上で動作するプログラムを作成する必要があります。チューニングを繰り返し、アプリケーションに適したSoCを探索する必要があり、ほとんど特注のようなアーキテクチャとなるため、DSA (Domain Specific Architecture) と呼ばれたりします。当然、真の最適なアーキテクチャを探索するには無限時間かかってしまうので、一般的にはアプリケーションの処理時間のボトルネックとなる処理のみをPLにオフロードすることで妥協します。しかし、アプリケーションの処理時間はボトルネックに大きく依存する場合が多く、ボトルネックをオフロードするだけでも十分な高速化が見込めます。主な応用例として、FPGAは機械学習のアクセラレータとしてよく用いられており、処理時間のボトルネックとなる畳み込み層をPLにオフロードにすることにより、アプリケーションの速度性能を大幅に向上させています。こちらのアプローチに関しては、書籍で分かりやすく解説してありますので、そちらを参照してください。
問題概要
ABC 152 C - Low Elements
問題文
1,...,Nの順列P1,...,PNが与えられます。
次の条件を満たす整数i (1≦i≦N)の個数を数えてください。
・任意の j (1≦j≦i) に対して、Pi ≦ Pj
制約
・1≦N≦2×105
・P1,...,PNは1,...,Nの順列である。
・入力はすべて整数である。
・時間制限 : 2 sec
・メモリ制限 : 1024 MB
アルゴリズムの選択
TLE解法
まず、この問題の解法として、iを1からNまで変化させ、iより小さい番地j (1≦j≦i) のPjとPiの大小比較していき、Piよりも小さいPjが存在した場合は、フラグを下げるといったような解法が思いつきます。このような解法のC++プログラムを以下に記載します。
# include <bits/stdc++.h>
# define int long long
typedef long long ll;
using namespace std;
ll N, P[200000], ans=0;
signed main(){
cin >> N;
for(int i=0;i<N;i++) {
cin >> P[i];
int flag=1;
for(int j=0;j<i;j++) {
if(P[j]<P[i]) flag=0;
}
ans += flag;
}
cout << ans << endl;
return 0;
}
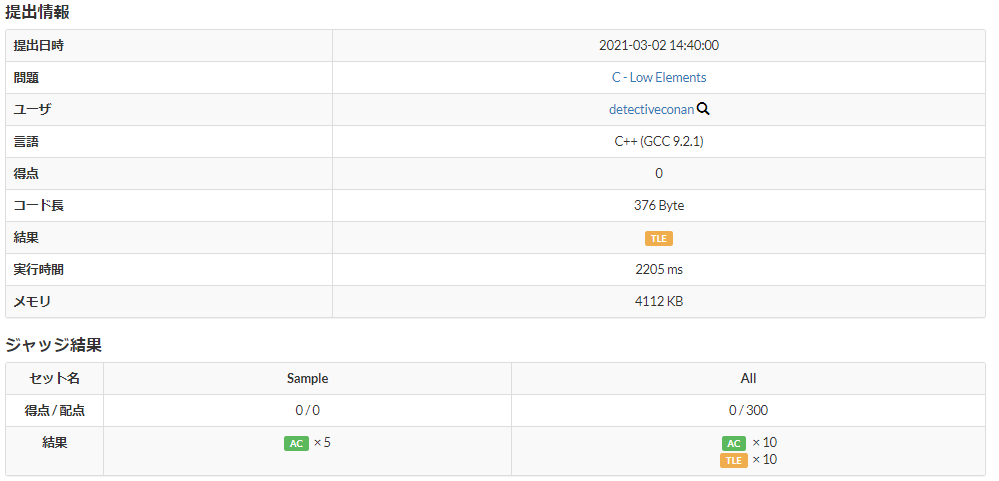
しかし、こちらのC++プログラムは2重ループが入っており、計算量はO(N2)となるため、Nの制約 (1≦N≦2×105) から2秒以内にプログラムを終了することができず、TLEとなってしまいます。
AC解法
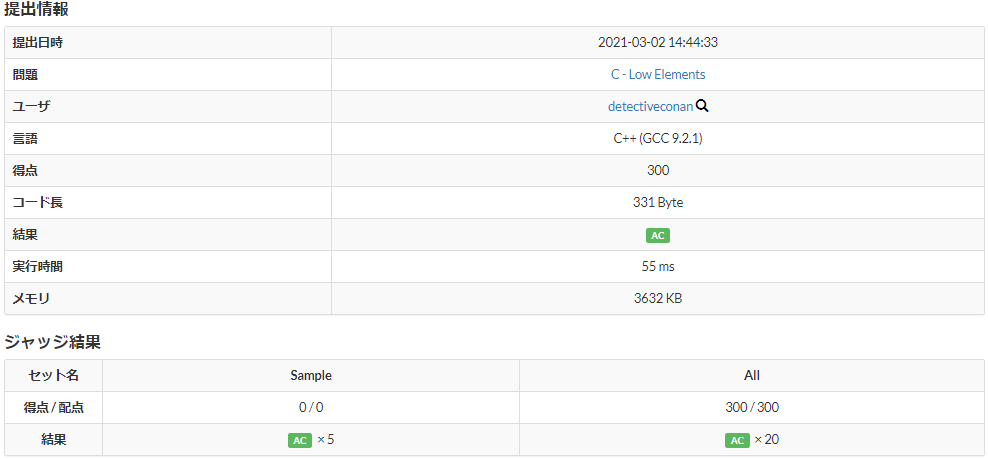
1つ目のソフトウェアレベルのアプローチでこの問題を考えていくと、AtCoderの公式解答解説にも書いてある通り、i番地までの最小値を記憶しながら、Piと比較することによって解くことができるため2重ループは不要となり、計算量はO(N)となります。このように、より計算量の少ないアルゴリズムを選択することによって、2秒というプログラムの実行速度要件を満たすことができます。
# include <bits/stdc++.h>
# define int long long
typedef long long ll;
using namespace std;
ll N, minv = 200000, ans=0;
signed main(){
cin >> N;
for(int i=0;i<N;i++) {
int a;
cin >> a;
minv = min(minv, a);
if(a<=minv) ans++;
}
cout << ans << endl;
return 0;
}
こうして、TLEしてしまったC++プログラムはなかったことにされるわけですが、この記事では、TLEしてしまったC++プログラムをHLSを使ってチューニングを行い、ハードウェア化することによって実行速度を向上させていきます。
おわりに
今回の記事では導入編ということで、アプリケーション高速化の2通りのアプローチとソフトウェアレベルでのプログラムの高速化について説明しました。次の記事で、HLSを使ったアルゴリズムのハードウェア化について説明していきます。
"TLE解法を救いたい"