【ライブラリは使わない!?】NNをライブラリなしで実装してみよう

内容

MNISTの数字識別をTensorFlowやPyTorch, scikit-learnなどのニューラルネット用ライブラリを使わずに実装してみたものです.
一度NumPyだけで実装してみると中で何を行っているのか分かって良い経験になります.
ただし, NumPyなどの基本的なライブラリは使用してもよいことにします.
ニューラルネットのブラックボックスを理解することを目的とします.

参考図書 : oreilly-japan/deep-learning-from-scratch

ディレクトリ構造

次のようにディレクトリを作成しました.

~/mnist

mnist
├── data
│   ├── arr
│   │   ├── params
│   │   ├── test
│   │   └── train
│   ├── output
│   └── ubyte
└── src
    ├── compare.py
    ├── func.py
    ├── layers.py
    ├── learning.py
    ├── make_dataset.py
    ├── make_noise.py
    └── research.ipynb

データセットのnumpy.ndarrayへの変換

今回はデータセットとして, MNISTを用います.
THE MNIST DATABASE of handwritten digits

(oreilly-japan/deep-learning-from-scratchでは関数が用意されていますが, これは基本ライブラリではないため, 今回は使用不可としました)

まずは, byte形式でデータセットをダウンロードします. ~/mnist/data/ubyte/で以下を実行します.

MacOSの場合

$ curl -O http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
$ curl -O http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
$ curl -O http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
$ curl -O http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz

Linuxの場合

$ wget http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz

これをnumpy.ndarrayに変換します.

ファイルのフォーマットは先のMNISTのサイトから見れます.

ザッとまとめると, labelの方はoffsetが8, imageの方がoffsetが16になっています.
labelは0~9の数字が入っているので基本的にはone_hot表現を, imagesは行をデータ数, 列をデータ次元(ピクセル数)にし, 0~255の画素値を0~1の浮動小数に正規化するように前処理しておきましょう. 後にノイズ耐性を見るためにノイズを加えたデータも処理するので, ファイル名を統一しておいた方が可読性が上がります. ということで"_noise0%"が付いています.

make_arr.py

import numpy as np
import gzip


def load_label(one_hot=True, label_num=10):
    filename_lst = ['train-labels-idx1-ubyte.gz', 't10k-labels-idx1-ubyte.gz']

    for filename in filename_lst:
        filepath = "../data/ubyte/"+filename

        with gzip.open(filepath, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)

        if one_hot:
            labels = np.eye(label_num)[labels]

        if "train" in filename: savepath = "../data/arr/train/train_T.npy"
        else: savepath = "../data/arr/test/test_T.npy"

        np.save(savepath, labels)


def load_image():
    filename_lst = ['train-images-idx3-ubyte.gz', 't10k-images-idx3-ubyte.gz']

    for filename in filename_lst:
        filepath = "../data/ubyte/"+filename

        with gzip.open(filepath, 'rb') as f:
            images = np.frombuffer(f.read(), np.uint8, offset=16)

        images = images.reshape(-1, 28*28)

        images = images/255

        if "train" in filename: savepath = "../data/arr/train/train_X_noise0%.npy"
        else: savepath = "../data/arr/test/test_X_noise0%.npy"

        np.save(savepath, images)


if __name__ == "__main__":
    load_label()
    load_image()

これを実行すると, 次のように~/mnist/data/arr/のところにnpyファイルが出来るはずです.

~/mnist/data/arr/

arr
├── test_X_noise0%.npy #評価用の入力データ
├── test_T.npy # 評価用の教師ラベルデータ
├── train_X_noise0%.npy #訓練用の入力データ
└── train_T.npy # 訓練用の教師ラベルデータ

これらのデータは次のような形式になっています.

  X =  \left(
    \begin{array}{c}
      \text{img array 1} \\
      \text{img array 2} \\
      \vdots \\
      \text{img array N} \\
    \end{array}
  \right) 
  \in \Re^{\text{データ数}N\times \text{次元}d}

今回の次元は, $d = 28\times28=784$になります. ndarray.shapeをすると確認出来ます.
以降, データ処理はほぼほぼ行列形式で行うことになります.

なお, 教師ラベルはone_hot=Trueとすることで, one-hot表現になっています.

出力関数の作成

出力関数は, "恒等関数"と"softmax関数"の2種類があります. 分類問題では後者の関数を使います.
これは分類結果の確率を表現しています.

\text{softmax} (\boldsymbol{x}) = \displaystyle \frac{\exp(\boldsymbol{x})}{\sum \exp(\boldsymbol{x})}

ベクトルを入力してベクトルが返ってきます. これをデータごとに行います. すなわち,

\text{softmax}(X) = \left(
    \begin{array}{c}
      \frac{\exp(\text{img array 1})}{\sum \exp(\text{img array 1})} \\
      \frac{\exp(\text{img array 2})}{\sum \exp(\text{img array 2})} \\
      \vdots \\
      \frac{\exp(\text{img array N})}{\sum \exp(\text{img array N})} \\
    \end{array}
  \right)
        = 
 \left(
    \begin{array}{c}
      \text{softmax(img arr 1)} \\
      \text{softmax(img arr 2)}\\
      \vdots \\
      \text{softmax(img arr N)}\\
    \end{array}
  \right) \in \Re^{\text{データ数}N\times\text{分類数}10}

softmax(img arr 1)は画像データ1に対して, (0の確率, 1の確率, ... , 9の確率) のような行ベクトルになっています.
これをnumpyを使って簡潔に書いていきます. 実際にこれを素直に書いてみるとオーバーフローしてしまうので,

\begin{aligned} 
\text{softmax} (\boldsymbol{x})_k =
\frac { \exp \left( \boldsymbol{x} _ { k } \right) } { \sum _ { i = 1 } ^ { n } \exp \left( \boldsymbol{x} _ { i } \right) } & = \frac { C \exp \left( \boldsymbol{x} _ { k } \right) } { C \sum _ { i = 1 } ^ { n } \exp \left( \boldsymbol{x} _ { i } \right) } \\ & = \frac { \exp \left( \boldsymbol{x} _ { k } + \log C \right) } { \sum _ { i = 1 } ^ { n } \exp \left( \boldsymbol{x} _ { i } + \log C \right) } \\ & = \frac { \exp \left( \boldsymbol{x} _ { k } + C ^ { \prime } \right) } { \sum _ { i = 1 } ^ { n } \exp \left( \boldsymbol{x} _ { i } + C ^ { \prime } \right) } \end{aligned}

を使って変形します. 具体的には$C$を各行の最大値とするのが良さそうです.
以下, 行列処理です.

oreilly-japan/deep-learning-from-scratchでは次のようになっています.

func.py

def softmax2(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

もう少し直感的に書き直してみたところ, 若干こちらの方が早かったです. 簡単なarrayを作ってみて試してみると簡単にわかります.

func.py

def softmax(Z):
    # 1次元ベクトルの場合
    if Z.ndim == 1:
        const = np.nanmax(Z)
        return np.exp(Z-const)/np.sum(np.exp(Z-const))
    # 行列の場合
    elif Z.ndim == 2:
        Z = (Z.T-np.max(Z,axis=1)).T
        Y = np.exp(Z)/np.sum(np.exp(Z), axis=1).reshape(Z.shape[0],-1)
        return Y
    # テンソルの場合
    else:
        raise ValueError
        print("Dimension Error !")

損失関数の作成

分類問題では損失関数は$E = - \frac { 1 } { N } \displaystyle\sum _ { n } \sum _ { k } t _ { n k } \log y _ { n k }$なる交差エントロピー誤差関数を用います.

func.py

def cross_entropy_error(Y, T):
    # 1次元ベクトルの場合
    if Y.ndim == 1:
        T = T.reshape(1, T.size)
        Y = Y.reshape(1, Y.size)
    
    batch_size = Y.shape[0]
    delta = 1e-7
    
    return -np.sum(T*np.log(Y+delta)) / batch_size

1次元の場合も行列と同じように計算できるようにするために, 見た目の形は変わらないものの, reshapeしてデータ形式を変えておきます.
行列はそのまま掛け算するとアダマール積$\bigodot$となります.

>>> x = np.array([[1,2], [3,4]])
>>> t = np.array([[10,-10], [10,-10]])
>>> y = t*x
>>> y
array([[ 10, -20],
       [ 30, -40]])

一応, オーバーフローを防止するためにdelta項を追加しました.
oreilly-japan/deep-learning-from-scratchにはありませんでしたが, 追加した方が発散しなくて良いでしょう.

各層の設計思想

今回は3層NNを実装します.
各層はクラスとして設計していきます. 作成するクラスは, "Affine", "ReLU", "SoftmaxWithLoss", 使用する関数は"relu", "softmax", "cross_entropy_error"と行列計算となります.

X \rightarrow \fbox{Affine1:($XW_1+B_1$)} \rightarrow Z_1 \rightarrow \fbox{ReLU:(relu($Z_1$))} \rightarrow X_2 \rightarrow \fbox{Affine2:($X_2W_2+B_2$)} \rightarrow Z_2 \rightarrow  \fbox{SoftmaxWithLoss:(softmax($Z_2$) $\rightarrow$ $Y$ $\rightarrow$ cross_entropy_error($Y$) $\rightarrow$ $L$)}  

基本的には, 入力行列を$X$, 出力行列を$Z$, 重み行列を$W$, バイアス行列を$B$, 分類結果の行列を$Y$, 誤差行列を$L$としていて, これ以降もこの変数に従って書いていきます. 加えて, データ数を$N$, データの次元を$d$とします.

参考図書では計算式を簡略化して計算グラフで考えているので, こちらでは数式で追ってみましょう.

classを設計する上でのポイントがあります.
学習させる時を念頭に置くことです. まずはforwardで分類結果を出し, そのあとbackwardで学習に用いる勾配を求めるという流れです. ですから, backwardで用いる値はメンバ変数に格納, すなわち, self.~で保存しておく必要があります.

Affine層

$\mathbf{Z} = \mathbf{X}\mathbf{W} + \mathbf{B} $ に対して,

\frac { \partial L } { \partial \mathbf{W} } = \mathbf{X} ^ { T } \frac { \partial L } { \partial \mathbf{Z} }\\
\frac { \partial L } { \partial \mathbf { X } } = \frac { \partial L } { \partial \mathbf { Z } } \mathbf { W } ^ { \mathrm { T } }

となる. これに関して一発でさらっと理解できる人はなかなかいないはずなので, 補足しておきます.
$\mathbf{Z}\in\Re^{N\times l}$とします.

$x_{nj}$は(画像)データ$n$の $i$番目の量で, $w_{ij}$は$i$番目の量と出力の$j$番目の値の重みです.

\mathbf{X}\mathbf{W} + \mathbf{B} = \\
 \left(
    \begin{array}{cccc}
      x_{11} & x_{12} & \dots & x_{1d}  \\
      \vdots & \vdots & \vdots & \vdots \\
      x_{N1} & x_{N2} & \dots & x_{Nd}  \\
    \end{array}
  \right)

 \left(
    \begin{array}{cccc}
      w_{11} & w_{12} & \dots & w_{1l}  \\
      \vdots & \vdots & \vdots & \vdots \\
      w_{d1} & x_{d2} & \dots & x_{dl}  \\
    \end{array}
  \right)

+

\left(
    \begin{array}{cccc}
      b_{11} & b_{12} & \dots & b_{1l}  \\
      b_{11} & b_{12} & \dots & b_{1l}  \\
      \vdots & \vdots & \vdots & \vdots \\
      b_{11} & b_{12} & \dots & b_{1l}  \\
    \end{array}
  \right)\\

 = 

\left(
    \begin{array}{ccc}
      x_{11}w_{11}+x_{12}w_{21}+\dots+x_{1d}w_{d1}+b_{11} & \dots & x_{11}w_{1l}+x_{12}w_{2l}+\dots+x_{1d}w_{dl}+b_{1l} \\
      \vdots & \vdots & \vdots & \\
      x_{N1}w_{11}+x_{N2}w_{21}+\dots+x_{Nd}w_{d1}+b_{11} & \dots & x_{N1}w_{1l}+x_{N2}w_{2l}+\dots+x_{Nd}w_{dl}+b_{1l}  \\
    \end{array}
  \right)

また,

\mathbf{X} ^ { T } \frac { \partial L } { \partial \mathbf{Z} } = 
 \left(
    \begin{array}{cccc}
      x_{11} & x_{12} & \dots & x_{1d}  \\
      \vdots & \vdots & \vdots & \vdots \\
      x_{N1} & x_{N2} & \dots & x_{Nd}  \\
    \end{array}
  \right)^T

 \left(
    \begin{array}{cccc}
      \delta_{11} & \delta_{12} & \dots & \delta_{1l}  \\
      \vdots & \vdots & \vdots & \vdots \\
      \delta_{N1} & \delta_{N2} & \dots & \delta_{Nl}  \\
    \end{array}
  \right)\\
=
\left(
    \begin{array}{ccc}
    x_{11}\delta_{11}+\dots+x_{N1}\delta_{N1} & \dots & x_{11}\delta_{1l}+\dots+x_{N1}\delta_{Nl}\\
    \vdots & \vdots & \vdots \\
    x_{1d}\delta_{11}+\dots+x_{Nd}\delta_{Nd} & \dots & x_{1d}\delta_{1l}+\dots+x_{Nd}\delta_{Nl}\\ 
    \end{array}
  \right)

なお, $\delta_{ni}$は$ \frac{\partial L}{\partial z_{ni}}$で, データ$n$の$i$番目の出力に対する誤差です.

こうして具体的に計算してみると, $x_{11}\delta_{11}+\dots+x_{N1}\delta_{N1}$ は1番目の量から1番目の出力に対する誤差の, 全データによる総和です.
従って, データ数で割らなければなりませんが, それはSoftmaxWithLoss層で割ることで調整しています(誤差は掛け算で伝播していくので一度どこかでかければ大丈夫です).

同じ要領でもう１つも計算してみましょう.

\frac { \partial L } { \partial \mathbf { Z } } \mathbf { W } ^ { \mathrm { T } }
=
 \left(
    \begin{array}{cccc}
      \delta_{11} & \delta_{12} & \dots & \delta_{1l}  \\
      \vdots & \vdots & \vdots & \vdots \\
      \delta_{N1} & \delta_{N2} & \dots & \delta_{Nl}  \\
    \end{array}
  \right)

 \left(
    \begin{array}{cccc}
      w_{11} & w_{12} & \dots & w_{1l}  \\
      \vdots & \vdots & \vdots & \vdots \\
      w_{d1} & x_{d2} & \dots & x_{dl}  \\
    \end{array}
  \right)^T\\

=
 \left(
    \begin{array}{ccc}
      \delta_{11}w_{11}+\delta_{12}w_{12}+\dots+\delta_{1l}w_{1l} & \dots & \delta_{11}w_{d1}+\delta_{12}w_{d2}+\dots+\delta_{1l}w_{dl} \\
      \vdots & \vdots & \vdots\\
      \delta_{N1}w_{11}+\delta_{N2}w_{12}+\dots+\delta_{Nl}w_{1l} & \dots &        \delta_{N1}w_{d1}+\delta_{N2}w_{d2}+\dots+\delta_{Nl}w_{dl} \\
    \end{array}
  \right)

これも同じく, 例えば$\delta_{11}w_{11}+\delta_{12}w_{12}+\dots+\delta_{1l}w_{1l}$は入力$x_{n1}$による誤差の総和でとなっています.

\frac { \partial L } { \partial \mathbf { B } } = \frac { \partial L } { \partial \mathbf { Z } }

こちらは自明です.

実際には連鎖律を考えながら, 行列の次元が適切になるように適当に転置して上手い具合に掛けてしまえば大丈夫ですが, 行列周りはややこしくなりがちなので一度計算しておきました.

それではコードの方に行きましょう.
oreilly-japan/deep-learning-from-scratchとは可読性を向上させるため, 微妙に変えているので注意してください.

layers.py

class Affine:
    def __init__(self, W, B):
        self.W = W
        self.B = B
        self.X = None
        self.dW = None
        self.dX = None
        
    def forward(self, X):
        self.X = X
        Z = np.dot(X, self.W) + self.B
        
        return Z
    
    def backward(self, error):
        self.dX = np.dot(error, self.W.T)
        self.dW = np.dot(self.X.T, error)
        self.dB = np.sum(error, axis=0)
        next_error = self.dX
        return next_error

このnext_errorが先の計算でいう$\delta$です.

ReLU層

forwardは以下の式で表されます.

x = \left\{ \begin{array} { l l } { z } & { ( z > 0 ) } \\ { 0 } & { ( z \leqq 0 ) } \end{array} \right.

backwardはこれの微分を考えて,

\frac { \partial x } { \partial z } = \left\{ \begin{array} { l l } { 1 } & { ( z > 0 ) } \\ { 0 } & { ( z \leqq 0 ) } \end{array} \right.

実装のポイントはmask変数を使って符号を取ることです. また, backwardでも符号が必要なのでこのmask変数はメンバ変数に格納する必要があります.

layers.py

class ReLU:
    def __init__(self):
        self.mask = None
    
    def forward(self, Z):
        self.mask = (Z<=0)
        X = Z.copy()
        X[self.mask] = 0
        
        return X
    
    def backward(self, error):
        error[self.mask] = 0
        next_error = error
        
        return next_error

こちらも特に補足することはありません.

SoftmaxWithLoss層

\displaystyle \frac{\partial L}{\partial \boldsymbol{Z}} = \boldsymbol{Y} - \boldsymbol{T}

となります. 数式で追っていきましょう.

\begin{array} { l } { Z \quad = \left( \boldsymbol{z _ { 0 }} , \ldots , \boldsymbol{z _ { 9 }} \right) } \\ { z = \left( z _ { 0 } , \ldots , z _ { 9 } \right) } \\ { L = - \displaystyle\sum _ { k } t _ { k } \log y _ { k } } \\ { y _ { k } =\displaystyle \frac { e ^ { z _ { 0 } } } { e ^ { z _ { 0 } } + \ldots + e ^ { z _ { 9 } } } = \displaystyle\frac { e ^ { z _ { k } } } { S } } \end{array}

これに対して考える.

\begin{aligned} \frac { \partial L } { \partial Z _ { k } }  = \frac { \partial L } { \partial y _ { k } } \frac { \partial y _ { k } } { \partial Z _ { k } } + \sum _ { j \neq k } \frac { \partial L } { \partial y _ { j } } \frac { \partial y _ { j } } { \partial Z _ { k } } \\ = - \frac { t _ { k } } { y _ { k } } \cdot \left( 1 - y _ { k } \right) + \sum _ { j \neq k } \left( - \frac { t _ { j } } { y _ { j } } \right) \left( - y _ { k } \cdot y _ { j } \right) \\ = - t _ { k } \left( 1 - y _ { k } \right) + \sum _ { j \neq k } t _ { j } y _ { k } \end{aligned}

ここで, $k$ が正解ラベルの場合, $t_k = 1, t_j = 0$ を考えて,

\frac { \partial L } { \partial Z _ { k } } = - 1 \cdot \left( 1 - y _ { k } \right) + \sum _ { j \neq k } 0 \cdot y _ { k } = y _ { k } - 1 = y _ { k } - t _ { k }

$i \neq k $が正解ラベルの場合, $t_k = t_{j\neq i }= 0,t_i = 1 $を考えて,

\frac { \partial L } { \partial Z _ { k } } = - 0 \cdot \left( 1 - y _ { k } \right) + y _ { k } + \sum _ { j \neq k , i } 0 \cdot y _ { k } = y _ { k } = y _ { k } - t _ { k }

いずれも同じで, ベクトル, 行列表示すれば,

\displaystyle\frac { \partial L } { \partial \boldsymbol{z} } = \boldsymbol{y} - \boldsymbol{t}\\
\displaystyle \frac{\partial L}{\partial \boldsymbol{Z}} = \boldsymbol{Y} - \boldsymbol{T}

layers.py

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.Y = None
        self.T = None
    
    def forward(self, Z, T):
        self.T = T
        self.Y = softmax(Z)
        self.loss = cross_entropy_error(self.Y, self.T)
        
        return self.loss
    
    def backward(self):
        batch_size = self.T.shape[0]
        dZ = (self.Y-self.T) / batch_size
        
        return dZ

Affine層で述べた通り, batch_sizeで割るのを忘れないようにしましょう.

networkの構築

参考図書と変えているところが複数あるので注意してください. load_params_dictはdict型の学習済みパラメータを使いたい場合のオプションです.

layers.py

class Neuralnet:
    def __init__(self, input_size=28*28, hidden_size_list=[100], output_size=10, weight_init_std=0.1, load_params_dict=None):
        self.parameters = {}

        self.parameters['W1'] = weight_init_std * np.random.randn(input_size, hidden_size_list[0])
        self.parameters['B1'] = np.zeros(hidden_size_list[0])


        self.parameters['W2'] = weight_init_std * np.random.randn(hidden_size_list[0], output_size)
        self.parameters['B2'] = np.zeros(output_size)

        if load_params_dict:
            self.parameters['W1'] = load_params_dict['W1']
            self.parameters['B1'] = load_params_dict['B1']
            self.parameters['W2'] = load_params_dict['W2']
            self.parameters['B2'] = load_params_dict['B2']

        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.parameters['W1'], self.parameters['B1'])
        self.layers['ReLU'] = ReLU()
        self.layers['Affine2'] = Affine(self.parameters['W2'], self.parameters['B2'])

        self.lastlayer = SoftmaxWithLoss()

    def pred(self, X):
        for layer in self.layers.values():
            X = layer.forward(X)
        Z = X

        return Z

    def pred_label(self, X):
        Z = self.pred(X)
        Y = np.argmax(Z, axis=1)

        return Y

    def loss(self, X, T):
        Z = self.pred(X)

        return  self.lastlayer.forward(Z, T)

    def acc(self, X, T):
        Z = self.pred(X)
        Y = np.argmax(Z, axis=1)
        data_num = X.shape[0]

        if T.ndim != 1:
            T = np.argmax(T, axis=1)

        acc = np.sum(Y==T) / float(data_num)

        return acc

    def grad(self, X, T):
        # FP : Forward Propagation
        self.loss(X, T)

        # BP : Backward Propagation
        error  = self.lastlayer.backward()
        layers_reverse = list(self.layers.values())
        layers_reverse.reverse()
        for layer in layers_reverse:
            error = layer.backward(error)

        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['B1'] = self.layers['Affine1'].dB
        grads['W2'] = self.layers['Affine2'].dW
        grads['B2'] = self.layers['Affine2'].dB

        return grads  

混同行列で可視化

どの数字をどの数字と誤認することが多いか調べるのに"混同行列"を評価として用いることがあります.
$i$行目, $j$列目は数字$i$を数字$j$と認識した回数です(可視化の際には正規化します).
なお, sklearnなどのライブラリにはもっとしっかりした関数が用意されています.

参考 : sklearn.metrics.confusion_matrix -- scikit-learn 0.20.2 documentation

どういうことかは上記を見ていただければわかると思います.

confusion_matrix.py

def confusion_matrix(true, pred, label_size=10):
    confusion_matrix = np.zeros((label_size, label_size)).astype(np.int)

    for t, p in zip(true, pred):
            confusion_matrix[t][p] += 1
    
    return confusion_matrix

データの読み込み

作成したNumPy.ndarayを読み込みます. 今はnoise_perは気にしなくて大丈夫です.

func.py

def load_mnist(noise_per=0):
    TRAIN_LABEL_DIR = "../data/arr/train/train_T.npy"
    TEST_LABEL_DIR = "../data/arr/test/test_T.npy"
    TRAIN_IMG_DIR = "../data/arr/train/train_X_noise"+str(noise_per)+"%.npy"
    TEST_IMG_DIR = "../data/arr/test/test_X_noise"+str(noise_per)+"%.npy"

    # 教師データの読み込み
    train_X = np.load(TRAIN_IMG_DIR)
    train_T = np.load(TRAIN_LABEL_DIR)

    # 評価データの読み込み
    test_X = np.load(TEST_IMG_DIR)
    test_T = np.load(TEST_LABEL_DIR)

    return train_X, train_T, test_X, test_T

特に難しいことはしていません.

パラメータの学習

学習プログラムは以下のようになりました. ノイズのあれこれは後ほど説明します.
$ python3 filename(保存ファイル名) iters_num(学習回数) lr(学習率) hidden_size_list(隠れ層ニューロン数) noise_per_max(今は0に設定) -debug(print文debug) -save(グラフ等の保存) で実行できます.

learning.py

import numpy as np
import matplotlib.pyplot as plt
import time
import sys
import pprint
from layers import Neuralnet
from func import load_mnist, confusion_matrix


# 学習
def learning(iters_num, lr, FILE_NAME, hidden_size_list, noise_per_max, debug, save):
    if debug: start = time.time()
    
    for noise_per in [i for i in range(0, noise_per_max+1, 5)]:

    # ----- データセットの読み込み -----
        train_X, train_T, test_X, test_T = load_mnist(noise_per)
        
        model = Neuralnet(hidden_size_list=hidden_size_list)
        train_size = train_X.shape[0]
        batch_size = 100
        
        train_loss_list = []
        train_acc_list = []
        test_acc_list = []

        tmp_train_loss_list = []
        tmp_train_acc_list = []
        tmp_test_acc_list = []
        
        for num in range(iters_num):
        # ----- batch処理 -----
            batch_mask = np.random.choice(train_size, batch_size)
            X_batch = train_X[batch_mask]
            T_batch = train_T[batch_mask]
            
        # ----- 勾配の算出 -----
            grads = model.grad(X_batch, T_batch)
            
        # ----- loss, accの算出 ------
            train_loss = model.loss(X_batch, T_batch)
            tmp_train_loss_list.append(train_loss)
            
            train_acc = model.acc(X_batch, T_batch)
            tmp_train_acc_list.append(train_acc)
            
            test_acc = model.acc(test_X, test_T)
            tmp_test_acc_list.append(test_acc)

        # ----- 10回の平均で計算する -----
            if num % 10 == 0:    
                avg_train_acc = np.mean(tmp_train_acc_list)
                avg_test_acc = np.mean(tmp_test_acc_list)
                avg_train_loss = np.mean(tmp_train_loss_list)

                train_acc_list.append(avg_train_acc)
                test_acc_list.append(avg_test_acc)
                train_loss_list.append(avg_train_loss)
                                                              
                tmp_train_loss_list = []
                tmp_train_acc_list = []
                tmp_test_acc_list = []

        # ----- 学習 -----
            for parameter in ('W1', 'B1', 'W2', 'B2'):
                model.parameters[parameter] -= lr * grads[parameter] 

        # ----- option -----
            if debug:
                percentage = int(100*(num+1)/iters_num)
                print("{}/{} : {}%".format(num+1, iters_num, percentage)) 
                print("train acc : {}".format(train_acc))
                print("test acc : {}".format(test_acc))
                print("train loss : {}".format(train_loss))
                print("\n", end="")

            if save:
                ACC_LOSS_FILE = "../data/output/"+FILE_NAME+"_noise"+str(noise_per)+"%_acc_loss.txt"
                with open(ACC_LOSS_FILE, mode='a') as f:
                    f.write("{}/{} : {}%\n".format(num+1, iters_num, percentage))
                    f.write("train acc : {}\n".format(train_acc))
                    f.write("test acc : {}\n".format(test_acc))
                    f.write("train loss : {}\n".format(train_loss))
                    f.write("\n")
        
        if save:
            plt.figure()
            p1, = plt.plot(train_acc_list)
            p2, = plt.plot(test_acc_list)
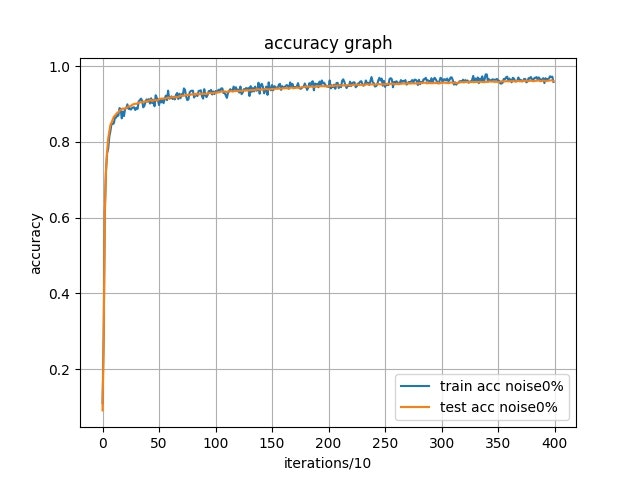
            plt.legend([p1, p2], ["train acc noise"+str(noise_per)+"%", "test acc noise"+str(noise_per)+"%"])
            plt.title("accuracy graph")
            plt.xlabel("iterations/10")
            plt.ylabel("accuracy")
            plt.grid()
            SAVE_ACC_DIR = "../data/output/"+FILE_NAME+"_noise"+str(noise_per)+"%_acc_graph.jpg"
            plt.savefig(SAVE_ACC_DIR)

            plt.figure()
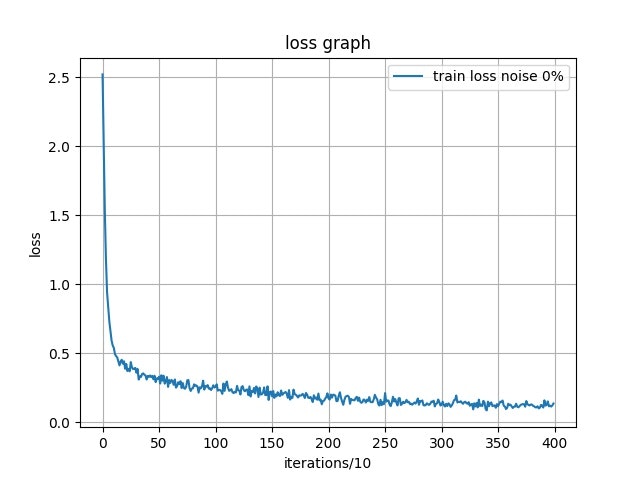
            p, = plt.plot(train_loss_list)
            plt.legend([p], ["train loss noise "+str(noise_per)+"%"])
            plt.xlabel("iterations/10")
            plt.ylabel("loss")
            plt.grid()
            plt.title("loss graph")
            SAVE_LOSS_DIR = "../data/output/"+FILE_NAME+"_noise"+str(noise_per)+"%_loss_graph.jpg"
            plt.savefig(SAVE_LOSS_DIR)
            
        # ----- 混同行列で可視化 -----    
            np.set_printoptions(threshold=100)
            pred = model.pred_label(test_X)

            # one-hot から vectorへ変換
            true = np.argmax(test_T, axis=1)
            CM = confusion_matrix(true, pred)
            CM_FILE = "../data/output/"+FILE_NAME+"_noise"+str(noise_per)+"%_cm.txt"
            np.savetxt(CM_FILE, CM, fmt='%d', delimiter=',')
            pprint.pprint(CM)

            #正規化
            min = CM.min(axis=1, keepdims=True)
            max = CM.max(axis=1, keepdims=True)
            CM = (CM-min)/(max-min)
            CM = 255*CM

            # 描画
            fig = plt.figure()
            ax = fig.add_subplot(111)
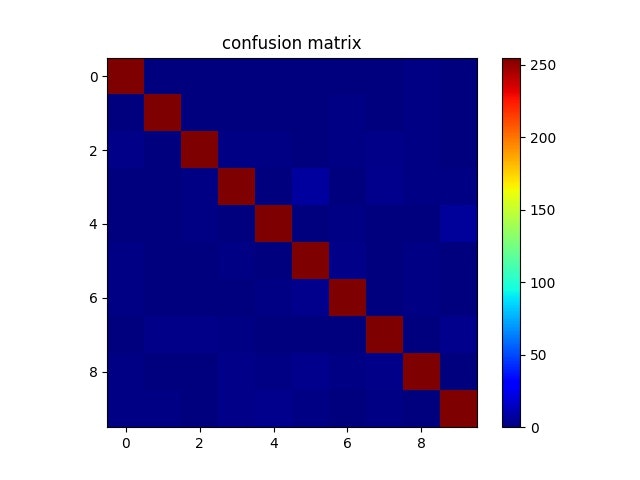
            ax.set_title("confusion matrix")
            img = ax.imshow(CM, cmap=plt.cm.jet)
            cbar = fig.colorbar(img, ax=ax)
            SAVE_CM_DIR = "../data/output/"+FILE_NAME+"_noise"+str(noise_per)+"%_cm_graph.jpg"
            plt.savefig(SAVE_CM_DIR)

        # ----- parameterの保存 -----
            WEIGHT_FILE1 = "../data/arr/params/"+FILE_NAME+"_weight1_noise"+str(noise_per)+"%.npy"
            np.save(WEIGHT_FILE1, model.parameters['W1'])
                                                                      
            BIAS_FILE1 = "../data/arr/params/"+FILE_NAME+"_bias1_noise"+str(noise_per)+"%.npy"
            np.save(BIAS_FILE1, model.parameters['B1'])
                                                                          
            WEIGHT_FILE2 = "../data/arr/params/"+FILE_NAME+"_weight2_noise"+str(noise_per)+"%.npy"
            np.save(WEIGHT_FILE2, model.parameters['W2'])
                                                                      
            BIAS_FILE2 = "../data/arr/params/"+FILE_NAME+"_bias2_noise"+str(noise_per)+"%.npy"
            np.save(BIAS_FILE2, model.parameters['B2'])

    if debug:
        elapsed_time = time.time()-start
        print("elapsed time : {}".format(elapsed_time))

if __name__ == "__main__":
    argc = len(sys.argv)
    FILE_NAME = sys.argv[1]
    iters_num = int(sys.argv[2])
    lr = float(sys.argv[3])
    hidden_size_list = [int(sys.argv[4])]
    noise_per_max = int(sys.argv[5])
    option = sys.argv[6:argc]

    debug = ("-debug" in option) 
    save = ("-save" in option)

    learning(iters_num, lr, FILE_NAME, hidden_size_list, noise_per_max, debug, save)

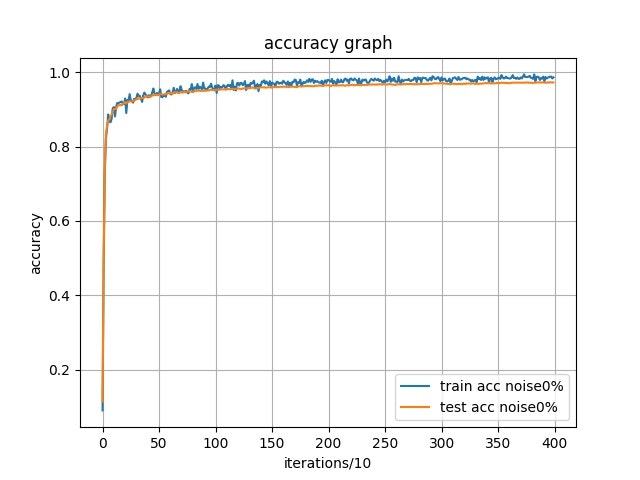
$ python3 learning.py sample 4000 0.1 100 0 -debug -saveで実行してみました.
このハイパラメータで学習させたところ, テストデータセットで正答率96%近くまで到達しました.

confusion_matrixの中身

 968,   0,   0,   0,   1,   2,   3,   2,   4,   0
   0,1116,   3,   2,   0,   1,   5,   2,   6,   0
   8,   1, 995,   5,   4,   0,   4,   9,   6,   0
   1,   0,   5, 950,   0,  27,   0,  13,   7,   7
   2,   0,   5,   0, 939,   1,   6,   2,   3,  24
   4,   1,   0,   4,   2, 867,   7,   0,   4,   3
   7,   3,   2,   0,   7,  13, 922,   0,   4,   0
   1,   9,  10,   4,   1,   1,   0, 988,   1,  13
   7,   2,   3,  11,   6,  13,   6,  10, 912,   4
   6,   7,   0,   8,  14,   5,   1,   7,   3, 958

混同行列を見ると, 4を9, 3を5と誤認識している率がやや高めな気がします. 可視化したグラフでもその部分が少し明るくなっているのがわかると思います. この２つは書き方や書く人によっては紛らわしいかもしれません. その辺りが影響していそうです.
このようなデータがありました.

一応左が4, 右が5ですが...左は9, 右は3に見えなくもないですね.

データの前処理

データの前処理として"ノイズ"を画像に入れてみましょう. 1%から25%までランダムに画素を選択し, ランダムな画素に置き換えます.

make_noise.py

from func import load_mnist
import numpy as np


def make_noise(width=28, height=28):
    train_X, train_T, test_X, test_T = load_mnist()
    data_size = width*height

    noise_per_list = [i for i in range(1, 26)]
    for SAVE_DIR in ["../data/arr/train/train_X_noise", "../data/arr/test/test_X_noise"]:

        for noise_per in noise_per_list:
            noise_num = int(0.01*noise_per*data_size)

            if "train" in SAVE_DIR: noise_X = train_X.copy()
            elif "test" in SAVE_DIR: noise_X = test_X.copy()

            for each_X in noise_X:
                noise_mask = np.random.randint(0, data_size, noise_num)

                for noise_idx in noise_mask:
                    each_X[noise_idx] = np.random.random()

            save_dir = SAVE_DIR+str(noise_per)+"%.npy"

            np.save(save_dir, noise_X)
            print("noise {}% is written.".format(noise_per))

if __name__ == "__main__":
    make_noise()

先ほどのlearning.pyの実行でnoise_per_maxを25にすると, 1%から25%まで, 5%刻みで学習させることができます.

ノイズ耐性の確認

それでは, ノイズを含んだ訓練データで学習したモデルと, クリーンな訓練データで学習したモデルが, ノイズを含むテストデータに対して正答率がどうなるか見ていきましょう.
テストデータのノイズは1%から25%まで, 1%刻みで見ていきます. モデルは5%から25%まで, 5%刻みのノイズを含む訓練データで学習したものを用います.

compare.py

import numpy as np
import matplotlib.pyplot as plt
from layers import Neuralnet
import time
import sys
from func import load_mnist
from collections import OrderedDict


def compare(FILE_NAME, debug=True, save=True):
    noise_per_list = [i for i in range(26)]
    load_params_dict_list = []

# ----- 各パラメータの読み込み -----
    for i in range(6):
        params_dict = OrderedDict()
        LOAD_W1 = "../data/arr/params/"+FILE_NAME+"_weight1_noise"+str(5*i)+"%.npy"
        LOAD_B1 = "../data/arr/params/"+FILE_NAME+"_bias1_noise"+str(5*i)+"%.npy"
        LOAD_W2 = "../data/arr/params/"+FILE_NAME+"_weight2_noise"+str(5*i)+"%.npy"
        LOAD_B2 = "../data/arr/params/"+FILE_NAME+"_bias2_noise"+str(5*i)+"%.npy"

        params_dict['W1'] = np.load(LOAD_W1)
        params_dict['B1'] = np.load(LOAD_B1)
        params_dict['W2'] = np.load(LOAD_W2)
        params_dict['B2'] = np.load(LOAD_B2)

        load_params_dict_list.append(params_dict)

    if debug: print("Finish loading parameters")

# ----- test_Xのノイズ耐性の調査 ----- 
    test_acc_list = []

    for i, load_params_dict in enumerate(load_params_dict_list):
        model = Neuralnet(load_params_dict=load_params_dict)
        test_acc_list_each = []
            
        for noise_per in noise_per_list:
            _, _, test_X, test_T = load_mnist(noise_per)
            test_acc = model.acc(test_X, test_T)
            test_acc_list_each.append(test_acc)

        test_acc_list.append(test_acc_list_each)
        if debug: print("{}% noise is written".format(i*5))

    # 描画
    plt.figure()
    graph = []
    graph_name = []
    for i, test_acc_list_each in enumerate(test_acc_list):
        p, = plt.plot(test_acc_list_each)
        graph.append(p)
        graph_name.append("noise "+str(5*i)+"%")
    plt.legend(graph, graph_name)
    plt.grid()
    plt.xlabel("test noise per")
    plt.ylabel("accuracy")
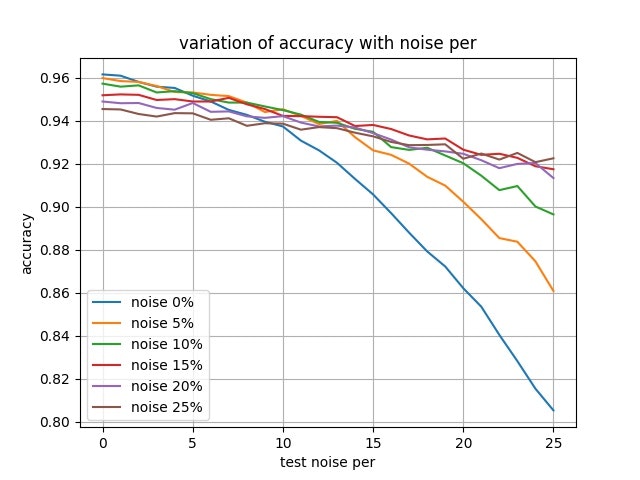
    plt.title("variation of accuracy with noise per")
    SAVE_DIR = "../data/output/"+FILE_NAME+"_compare.jpg"
    plt.savefig(SAVE_DIR)


if __name__ == "__main__":
    argc = len(sys.argv)
    FILE_NAME = sys.argv[1]
    option = sys.argv[2:argc]
    
    debug = ("-debug" in option)
    save = ("-save" in option)

    compare(FILE_NAME, debug=debug, save=save)

ノイズなしを0%と敢えて表記することでif分岐をなくすことができています.

グラフをみると, ノイズなし, すなわち, test noise perが0の部分はそれほどモデル間に差はありませんが, test noise perが増えるにつれて, ノイズを多く含んだ訓練データで学習したモデルの方が良い挙動を示しています.
つまり, 訓練データのノイズを含ませると, ノイズ耐性が上がると言えます.
さらに, データ数が少ない時にはデータの水増しの効果もあるでしょう.
適度にノイズを加えるのはロバスト性を上げるようです.

隠れ層の役割

ここから先は自分の解釈で正しいかどうか分かりません.

ニューロン数の増減は簡単に行えて, 実行時に hidden_size_list の値を変更するだけです. 基準として入力サイズの784より小さいか大きいかで比較します. 先ほどの実行時には100個のニューロンで行ったので今回は1200個で学習させてみましょう. これに関してはJupyter Notebookで対話形式で行いました.

research.ipynb

# # ニューロンの調査

# ノイズなし3層ニューラルネット
# iters_num=4000, lr=0.1, hidden_size_list=10で実行

# In[1]:


import numpy as np
import matplotlib.pyplot as plt
from func import load_mnist


# ## 重み行列の可視化

# ### $W_1$の可視化

# In[2]:


W1 = np.load("../data/arr/params/hidden10_weight1_noise0%.npy")
plt.figure(figsize=(10,5))
for idx in range(W1.shape[1]):
    W1_idx = W1[:, idx]
    W1_idx = W1_idx.reshape(28, 28)
    plt.subplot(2,5, idx+1)
    plt.title("idx{}".format(idx))
    plt.imshow(W1_idx, cmap="Greys")
plt.show();


# ### $W_1$の寄与の可視化

# In[3]:


W2 = np.load("../data/arr/params/hidden10_weight2_noise0%.npy")
plt.figure(figsize=(25,10))
for num in range(W2.shape[1]):
    W2_num = W2[:, num]
    plt.subplot(2, 5, num+1)
    plt.plot(W2_num)
    plt.grid()
    plt.xlabel("idx")
    plt.title("number{}".format(num))
    plt.xticks(np.arange(0, 10, 1))
plt.show();

これを見ると, 隠れ層のニューロンが多いと過学習気味になっていることがわかります.

次に重み行列を見ていきましょう. $\boldsymbol{W_1}$を可視化してみます.

次に, 各$\boldsymbol{W_1}$が各数字にどれだけ影響を及ぼしているかグラフにしてみます. 数字$k$が"好き好む" $\boldsymbol{W_1}$は$\boldsymbol{W_2}$の$k$列目を見ることで分かります.

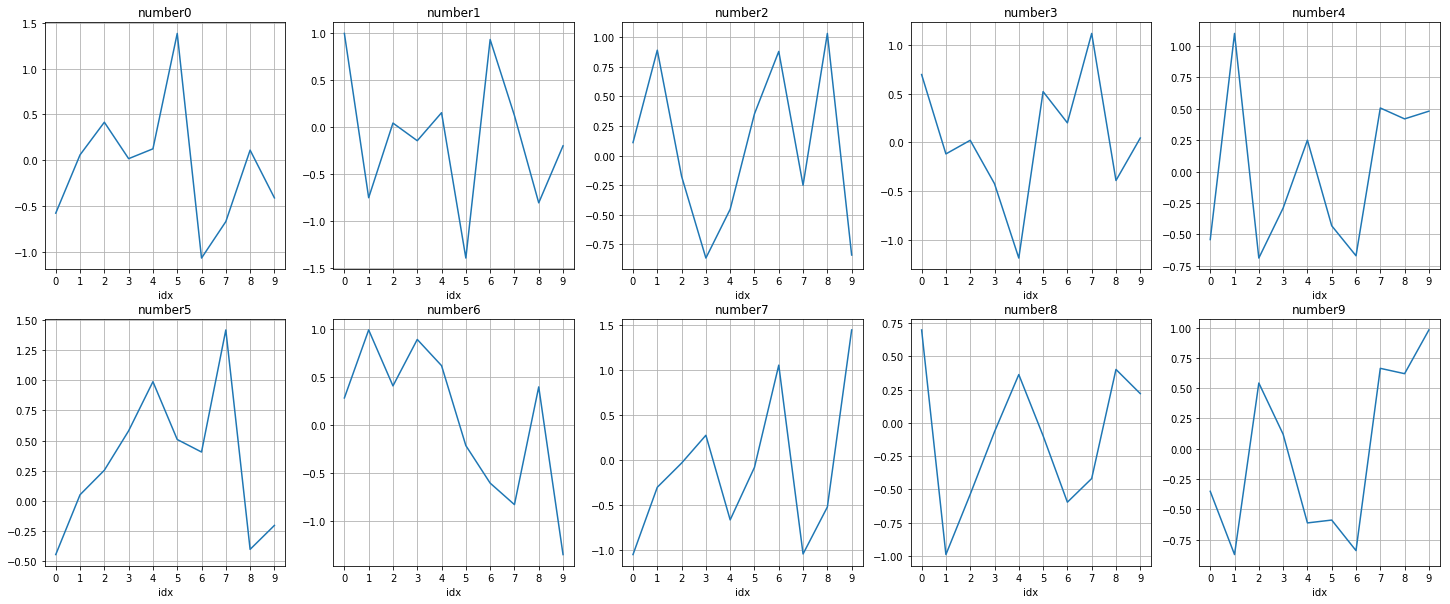
これを見ると, 次のような推測ができます. 分かりやすい例を挙げます. 数字 0 への $\boldsymbol{W_1}$の寄与を見ると, idx5 が非常に高いのに対して, idx6 は非常に低いです. idx5 と idx6 を見比べてみると, 中央付近に画素値が高いか低いかの違いが見受けられます. 数字 0 は中央付近の画素値は低いことが多いはずで, それが影響していると考えられます. つまり, 数字 0 は$\boldsymbol{W_1}$のidx5を"好み", idx6を”嫌う"傾向にあると言えます. 実際, 他の数字, 例えば数字 1 では逆転しているのが分かります(1は中央付近に画素値が集中します). このことから, 中間層 は入力データを一旦別の次元に変換して線形分離しやすい空間で処理を行っていると考えられます. つまり, 隠れ層はフィルターのようなもので自由にフィルター数を設定できる, と言ったイメージでしょうか.

それを踏まえたうえでニューロン数の増減を見てみると次のようなことが推測されます. 入力データより隠れ層のニューロン数が少なければ, 入力データはやや冗長であるため, 低次元に変換し, 逆に入力データより隠れ層のニューロン数が多ければ, 入力データでそのものでは足りず, より高次元に変換して処理を行うと考えられる. 次元を高めれば高めるほど線形分離しやすいことは言うまでもないですが, その分訓 練データにオーバーフィッティングする可能性も高まります. 過学習と正答率のバランスを考えて設定する必要があると言えそうです.