線形帰還シフトレジスタについてざっくり

疑似乱数という物をご存知だろうか？
確率的に値を生成する乱数とは違い、あたかもランダムで値を生成しているかの様に見せかけている物のことである。
この記事ではそんな疑似乱数にて使用される線形帰還シフトレジスタ（以下LFSRと呼ぶ）について、筆者が現在軽く群論をやっているので、群論も少し交えつつ解説していく

※筆者は情報系なので、数学的に厳密でない内容が含まれている場合があります。あらかじめご了承ください

前提知識1:群論の群とは

群とはざっくり言うと、集合と演算子の組み合わせの中で特定の条件を満たした物である

$G$を集合、$*$を演算子とすると、群の表し方としては以下の様になる

(G, *)

なお、特定の条件とは以下の3つである。
(i).$G$の任意の元$x$,$y$,$z$に対して

$(x * y) * z = x * (y * z)$

が成り立つ。これを結合律という
(ii).$G$の元$x$に対して

$x * e = e * x = x$

を満たす$e$が存在する
(iii).$G$の元$x$に対して

$b * a = a * b = e$

を満たす$b$が存在する

この様物を群という。（この記事においては群とは集合と何か操作をする演算子を組み合わせた抽象データ型の様な物という認識でいてくれれば良い）

前提知識2:巡回群

上で説明した群にも色々種類がある。
群の内$G$を集合としたとき、全ての元を$a^k(a\in G, k\in \mathbb N)$で表せる様な群を巡回群という。
例えば以下の様な物である。

集合$G = \lbrace1, i, -1, -i\rbrace$と演算子$\times$にて形成される群($G, \times$)は$i$をそれぞれの元に4回かけると以下の様に同じ値に戻ってくる。

$1\times i^4 = 1$
$i\times i^4 = i$
$-1\times i^4 = -1$
$-i\times i^4 = -i$

本記事においては、まるで回転の様に同じ値に戻ってくる群のことを巡回群というんだなぁ程度の認識で構わない

巡回群及び群の二つを踏まえ本題に入っていく

線形帰還シフトレジスタとは

ここから本題線形帰還シフトレジスタについてである。
線形帰還シフトレジスタ（以下LFSRと表記）とは、ある基準を基にフィードバックビットを割り出し、それを左シフトした後の入力ビットの最下位桁に代入する。という操作が定義されたシフトレジスタである。

ある基準については以下の図を使って説明していこうと思う。
以下の図は16ビットのビット列を入力ビットとするLFSRである。

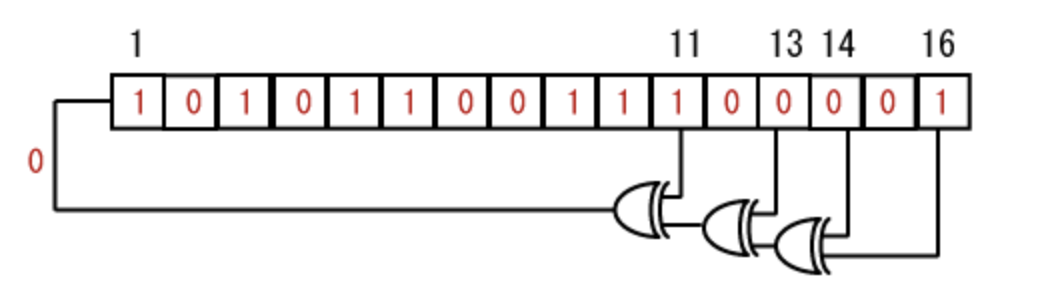
11,13,14,16からそれぞれ出力線が伸びていると思う。
この出力線が出ている部分をタップシーケンスといいこの部分同士でXORを取った値がそのままフィードバックビットとなる。
この操作を繰り返すことで初期の入力ビットに戻ってくる。つまり...巡回群であると言える。
ちなみに、このタップシーケンスの位置は入力ビットの桁数によって場所は変わる。

以下にその表を記述する。

ビット数	タップシーケンスの桁数
3	1, 3
4	3, 4
5	3, 5
6	5, 6
7	6, 7
8	4, 5, 6, 8
9	5, 9
10	7, 10
11	9, 11
12	4, 10, 11, 12
13	8, 11, 12, 13
14	2, 12, 13, 14
15	14, 15
16	11, 13, 14, 16

これだと数学的な解析が難しいのでタップシーケンスの部分を多項式で表すと（帰還多項式または原始多項式という）以下の様になる

ビット数	帰還多項式
3	$x^3 + x + 1$
4	$x^4 + x^3 + 1$
5	$x^5 + x^3 + 1$
6	$x^6 + x^5 + 1$
7	$x^7 + x^6 + 1$
8	$x^8 + x^6 + x^5 + x^4 + 1$
9	$x^9 + x^5 + 1$
10	$x^{10} + x^7 + 1$
11	$x^{11} + x^9 + 1$
12	$x^{12} + x^{11} + x^{10} + x^4 + 1$
13	$x^{13} + x^{12} + x^{11} + x^8 + 1$
14	$x^{14} + x^{13} + x^{12} + x^2 + 1$
15	$x^{15} + x^{14} + 1$
16	$x^{16} + x^{14} + x^{13} + x^{11} + 1$

実際の遷移が気になる場合は、以下のC++で書かれたコードを手元の環境にて動かしてもらえれば理解できると思う。

main.cpp

#include <iostream>
#include <string>
#include <bit>
#include <vector>
using ull = unsigned long long;

int main()
{
    ull n; // ビット数
    ull t; // フィードバックタップの数
    ull N; // 線形帰還シフトレジスタのステップ数
    std::cin >> n >> t >> N;
    std::string input_bits; // 入力ビット
    std::cin >> input_bits;
    // 文字列で取ってきた入力ビットを数字に変換
    ull state = 0;
    for (int i = 0; i < n; i++)
        state = (state << 1) | (input_bits[i] - '0');
    // フィードバックタップのマスクを作成
    ull feedback_mask = 0;
    for (int i = 0; i < t; i++)
    {
        int k;
        std::cin >> k;
        feedback_mask |= (1ULL << k);
    }
    // LFSRの動作を定義するラムダ式
    auto lfsr_step = [&](ull current_state) -> ull
    {
        // フィードバックタップ使用後のビットの数を見る
        ull feedback = __builtin_popcount(current_state & feedback_mask) % 2;
        current_state = ((current_state << 1) & (1ULL << n) - 1) | feedback;
        return current_state;
    };
    // 各ビットの遷移を格納する配列
    std::vector<ull> transitions(N, 0);
    // ステップ1
    transitions[0] = lfsr_step(state);
    // ステップ2~Nまで
    for (int k = 1; k < N; k++)
        transitions[k] = lfsr_step(transitions[k - 1]);
    std::string res = "";
    for (int k = 0; k < N; k++)
    {
        res += std::to_string(k + 1) + "番目の遷移は";
        for (int i = n - 1; i >= 0; i--)
            res += ((transitions[k] & (1ULL << i)) ? '1' : '0');
        res += "です\n";
    }
    std::cout << res << std::endl;
}

※おかしなところあるな・・・とかの場合はgithubに同様のコードあげてるのでプルリクください→(https://github.com/nokoken/Fibonacci_LFSR)

従って、帰還多項式の一般項は以下の様になる。
（$c_{n-1}...c_1は0
または1ただし、c_0のみ1となる$）

$f(x) = x^n + c_{n-1}x^{n-1}+・・・+c_1x+c_0$

一般項を見てもらうとわかるように巡回群になるかどうかは別にして、タップとして取れる多項式は無数に存在する。
よって、数ある中から選ぶ必要がある。

帰還多項式となることで全パターンを巡るため巡回群となり、疑似乱数生成器として機能する。

なお、帰還多項式となるには条件がある。
それは以下の3つである。

(i).不可約な多項式である。
(ii).$2^n-1$回の周期で巡回する（nは入力ビットの桁数）

それぞれ意味を説明すると・・・
(i)の"不可約な多項式である"とは言い換えると因数分解できない多項式であるという意味である。
因数分解ができる場合は、分解できた個々の多項式にて巡回群がそれぞれ生成されてしまうので同じ値が複数個出てきてしまう恐れがある。
したがって、不可約な多項式であることは絶対条件である。
(ii)の"$2^n-1$回の周期で巡回する（nは入力ビットの桁数）"とは全てのパターンを巡るというこのLFSRの特性そのものなので満たさなければLFSRと言えないからである。

最後に

意外とLFSRの記事が少ないので、ざっくりと解説したが...いかがだっただろうか？
数学やアルゴリズムの基本的な構造や理論が現実の通信や暗号技術などで活用されているという部分がCS全般に共通する魅力ではないだろうか？

追記
帰還多項式の表部分に+1が抜けておりました。
失礼しました。

参考サイト

https://ja.wikipedia.org/wiki/%E7%B7%9A%E5%BD%A2%E5%B8%B0%E9%82%84%E3%82%B7%E3%83%95%E3%83%88%E3%83%AC%E3%82%B8%E3%82%B9%E3%82%BF
https://qiita.com/kerupani129/items/58f337007cefd8d94c40
https://note.com/tmnkj/n/n09eed50e0523
https://www.youtube.com/watch?v=p03QyJc8gio