基本のSIRモデルで接触率(感染率)を周期的に変化させる
既出記事、「OpenModelicaで感染症の数理モデル「SIRモデル」を実装する(死亡率、再感染率を反映する)」で作成したモデルで 再感染率を周期的に変化させ、規制状態と緩和状態を繰り返すとどのようなグラフになるかシミュレーションしてみます。
このモデルの前提条件
- 基本のSIRモデルとし、死亡率、再感染率は 0とする
- ワクチンは使用しない
なお、以下のシミュレーションは全て仮のパラメータでモデルの検証をしただけであり、実際の数値を反映・予想したものではないことをお断りしておきます。
モデルの変更点
cl_SIRbetaInput の β値入力に TimeTableで 15日おきに 100%、20%(80%減)を繰り返す設定にします。60日以降は100%のままとします。
β値の変化をグラフ上で見やすくするために gainを追加して、100, 20 に変換。
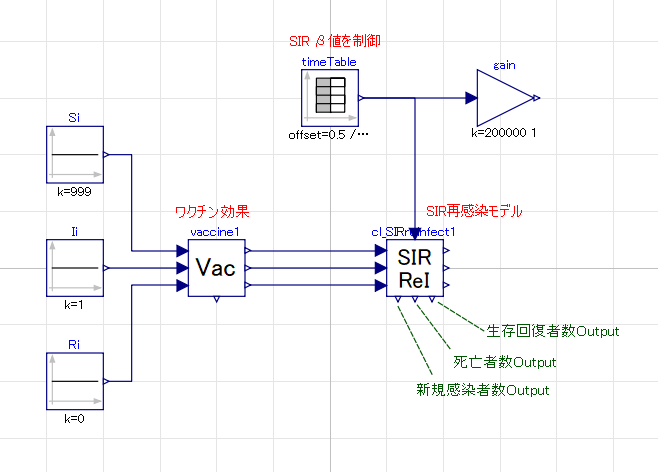
作成したモデル
シミュレーション結果
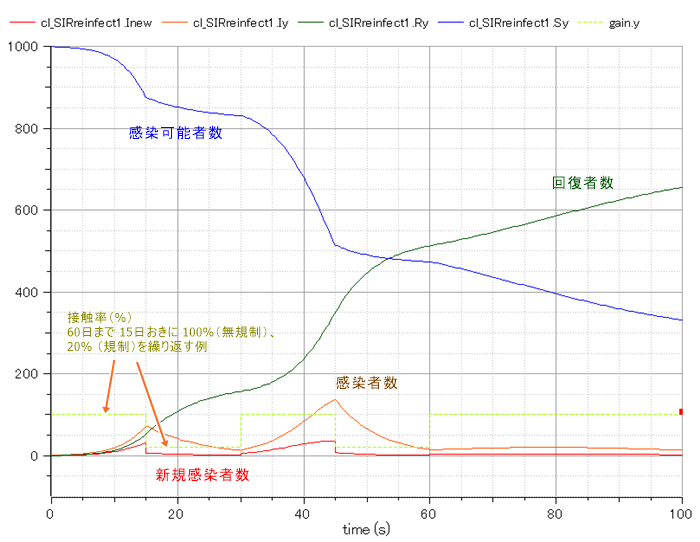
感染可能者、感染者、新規感染者、回復者をグラフで見る
感染者、新規感染者のみのグラフ
感染者の推移だけを拡大して確認します。
基本のSIRモデルで接触率を100%、20%と周期的に変化させると感染初期には規制を緩和した途端に新規感染者数が増加し始め、再度規制すると減少していくことが確認できます。
また、時間が経過して(グラフの60日目以降)回復者(抗体獲得者)が50%を超えるくらいに増えれば、接触率が高まっても新規感染者数は漸減していくようです。

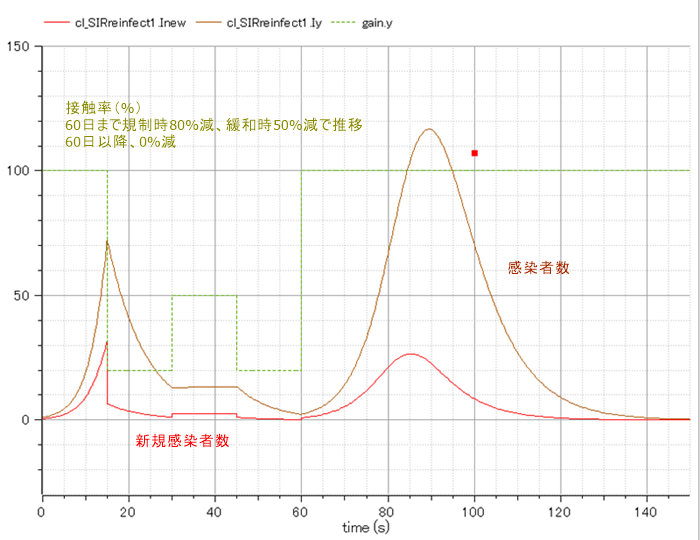
緩和時でも接触率を50%減程度に管理した場合のグラフ
60日までは管理した効果で抑えられているように見えます。
ただし、そこから緩めてしまうと新規感染者が激増します。
抗体獲得者が一定数に満たないうちに緩和するといけないようです。
関連記事
OpenModelicaで感染症の数理モデル「SIRモデル」を実装する
OpenModelicaで感染症の数理モデル「SIRモデル」を実装する(ワクチンの効果を見る)
OpenModelicaで感染症の数理モデル「SIRモデル」を実装する(死亡率、再感染率を反映する)
感染病の数学予測モデルの紹介 (SIRモデル)
OpenModelicaモデル
GitHub上で公開しました。
pk_SIRmodel.mo