感染病の数学予測モデルの紹介 (SIRモデル）

1.初めに

　2019年12月に中国武漢で発生した新型コロナウイルス(Convid-19)の日本における感染者数が増えいています。インフルエンザ, AIDS, SARS,などの感染病がどのように人間集団の中で拡大していくプロレスを理解することは、予防接種の設定、感染者の隔離などの保健政策の効果を確認するためにも重要です。
　ここで、感染病数学予測モデルの基本であるSIRモデルを紹介し、このモデルをPythonで計算する過程を紹介します。

追記：
プログラミングとは関係ない話ですが、2015年Nature詩に、新型コロナウイルスの流行を予測した論文が掲載されました。
今回の新型コロナウイルスの事態がどう収束していくのか、ヒントが得られる内容ですので、ご興味のある方は下記のリンクの記事も読んでいただければと思います。

2015年に新型コロナウイルスの流行を予測した論文の紹介
https://qiita.com/kotai2003/private/a44ca921314d17cc62e3

2.感染病の数学予測モデル(SIRモデル）

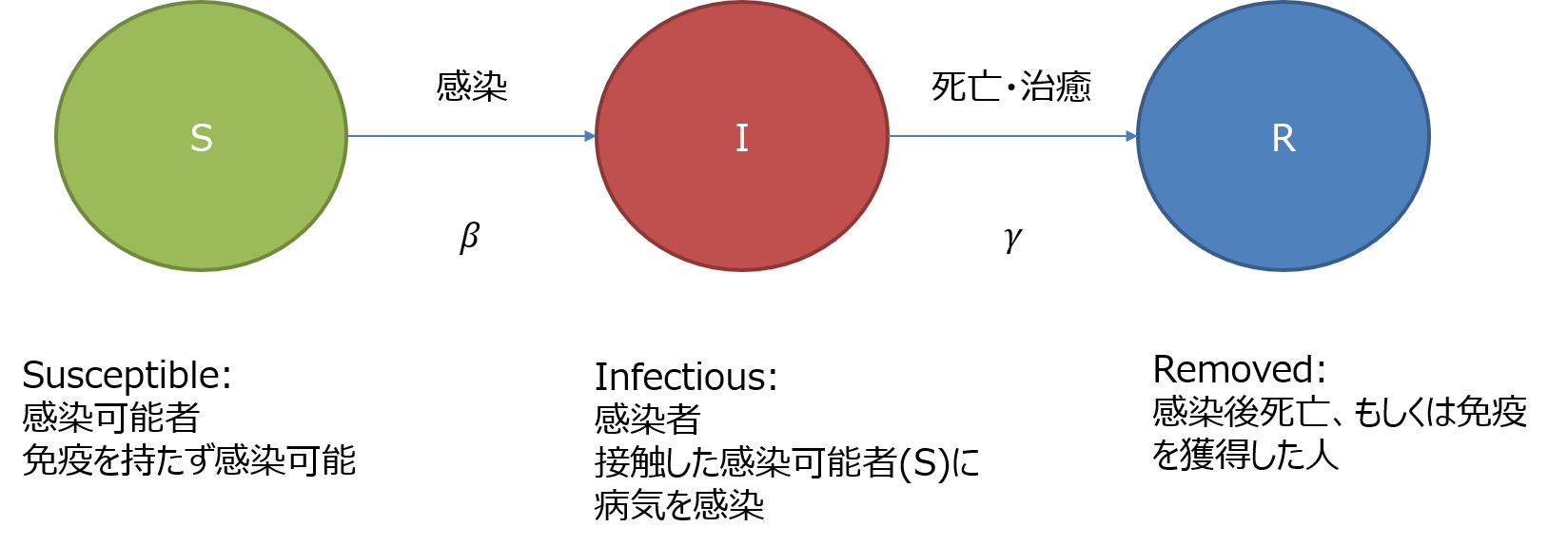
SIRモデルは、伝染病の流行プロセスを説明する基本モデルです。モデルの名称は、モデルの変数名のSusceptible, Infectious, Recoveredの頭文字に起因します。1927年　W.O. KermackとA.G. McKendrickの論文で初めて紹介されました。

SIRモデルでは、全体人口を次の集団に分類し、時間に関する各集団の人口増減を微分方程式で表します。　
- S(Susceptible) : 伝染病に対する免疫がない。感染可能者
- I Infectious)：感染により発病し、感染可能者(S)への伝染可能な者。感染者
- R (Removed) : 発病から回復し、免疫を獲得したもの。あるいは発病から回復できず死亡した者。（このモデルのシステムから排除されるため、Removedと言います。）

各集団の人口増減を次の微分方程式で表します。

\begin{align}

\frac{dS}{dt} &= -\beta SI \\
\frac{dI}{dt} &=  \beta SI -\gamma I \\
\frac{dR}{dt} &=  \gamma I \\

\end{align} 

\begin{align}
S &: 感染可能者 \quad \text{(Susceptible)}　\\
I &: 感染者 \quad \text{(Infectious)}　\\
R &: 感染後死亡者、もしくは免疫を獲得した者 \quad \text{(Removed)}　\\
\beta &: 感染率\quad \text{(The infectious rate)} \quad [1/day] \\
\gamma &:除去率\quad \text{(The Recovery rate)} \quad [1/day]　\\
\end{align}

このSIRモデルの前提条件
- 一度免疫を獲得した者は2度と感染することなく、免疫を失うこともない。
- 全体人口で外部からの流入及び流出はない。なお出生者及び感染以外の原因で死亡する者もいない。

3. SIRモデルの計算

SIRモデルは、数値積分を用いて解きます。ここでは、PythonのScipyモジュールのRunge-Kutta方程式を解くodeint関数を利用します。

import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
%matplotlib inline

次に、SIRモデルの微分方程式をodeintで計算できる形に記述しまうす。コードのv[0], v[1], v[2]は、それぞれS,I,Rに対応します。

#Define differential equation of SIR model

'''
dS/dt = -beta * S * I
dI/dt = beta * S * I - gamma * I
dR/dt = gamma * I

[v[0], v[1], v[2]]=[S, I, R]

dv[0]/dt = -beta * v[0] * v[1]
dv[1]/dt = beta * v[0] * v[1] - gamma * v[1]
dv[2]/dt = gamma * v[1]

'''
def SIR_EQ(v, t, beta, gamma):
    return [-beta*v[0]*v[1], beta * v[0] * v[1] - gamma * v[1], gamma * v[1]]

そして、数値積分に必要な各パラメータ及び初期条件を定義します。ここでは、人口1,000名の集団に対し、初期に感染者が1名がいたと仮定します。
感染率を0.2/1000に、除去率を0.1と設定します。

\begin{align}
\beta &=0.2/1000 \\
\gamma &=0.1 \\
\end{align} 

最後にBasic Reproduction NumberのR0を計算します。R0＞１の場合、この伝染病が収束せずに、拡大することを意味します。

#parameters
t_max = 160
dt = 0.01

beta_const = 0.2/1000
gamma_const = 0.1


#initial_state
S_0=999
I_0=1
R_0=0
ini_state = [S_0,I_0,R_0] #[S[0], I[0], R[0]]

#numerical integration
times =np.arange(0,t_max, dt)
args  =(beta_const, gamma_const)

#R0
N_total = S_0+I_0+R_0
R0 = N_total*beta_const *(1/gamma_const)
print(R0)

数値積分結果をresultに格納し、この結果を時間軸に対しプロットする。

#Numerical Solution using scipy.integrate
#Solver SIR model
result = odeint(SIR_EQ, ini_state, times, args)
#plot
plt.plot(times,result)
plt.legend(['Susceptible','Infectious', 'Removed'])

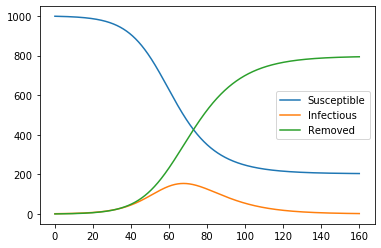
　このグラフから言えることは、1,000名の集団に1名の感染者(Infectious(0))が発生した場合、最終的に800名程度(Removed(160))が感染を経験することです。そして、感染者(Infectious)のピークは約70日辺りで発生し、その後は感染が収束することがわかります。
このように感染病に関するパラメータを利用し、感染病が人口集団に及ぼす影響を評価することが可能です。

4. 参考資料

-Coronavirus COVID-19 Global Cases
https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html?fbclid=IwAR2FwOf4Cjm4okosqFt0Ddr4k0dUgswM28oAqYkkVY6QT6BBCZQ1NlfPDXk#/bda7594740fd40299423467b48e9ecf6