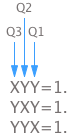IBMが公開しているIBM Q ExperienceのBeginners Guideをまあまあ読める程度の日本語に直しました.
IBM Q Experienceをいじりたいけど英語を読みたくない人向け+自分が大学で主催してる量子コンピュータの勉強会で「ほらほらこの記事」って言いながら見せるために投稿します.
※英語は決して得意ではないので,文章がおかしい箇所あればご指摘いただけると幸いです.
※画像はBeginners Guide本文から引用させていただきました.
※FAQ for biginnersは省略しています.
introduction -イントロダクション-
私たちは今,情報革命の新しいステージの始まりにいます.最初の情報革命は1950年ごろ,一握りの専門家だけが高価で巨大なコンピュータを使用できた時代に始まりました.今日,世界には人間よりも多くのコンピュータがあります.私たちは通信から輸送,商取引,そして(もちろん!)インターネットまで,あらゆるものにコンピュータを利用しています.コンピュータのさまざまな能力は,論理ゲートと呼ばれるAND,OR,NOTのような単純な操作を使って$0$と$1$を操作することによって生成されます.一度に何十億ものコンピュータが毎秒何十億という操作をすることによって,私たちの世界はより便利で,活気あるものになります.
35年以上にわたり,IBMは通常の「古典的」な情報とはまったく異なる種類の情報と情報処理を研究しています.「量子情報」と呼ばれるこの新しい種類の情報は,実際理解が可能で,また有用です。量子情報の基本単位はqubit(キュービットと読む),もしくは量子ビットと呼ばれ,量子ビットを記憶して処理するマシンは量子コンピュータと呼ばれます.私たちはこの数年間,より強力な量子コンピュータを構築し,テストしてきました.昨年,ヨークタウンの研究室で保管されている5量子ビットの量子コンピュータをインターネットで一般に公開しました.言い換えれば、プログラマブルな量子コンピュータがあなたの手元にあります!間もなく公開している量子コンピュータをアップグレードする予定ですが,量子計算を感じるには5量子ビットでも十分です.
1900年代初頭に生まれた量子論は,原子や電子のような小さな粒子の奇妙な振る舞いをうまく説明することによって,物理学と化学に革命をもたらしました.20世紀後半にはこれらの粒子だけでなく,情報そのものにも量子論が適用されることが発見されました.これは情報処理の科学技術に革命をもたらし,新しいタイプの計算とコミュニケーションへの扉を開きました.
私たちは,このBiginners guideを読んでいるあなたが量子計算とその新しい可能性についての知見を得ることを期待しています.新しい可能性の中には今までにない材料や薬物の設計,データベースの迅速な検索,高効率な線形方程式の解法など,現時点では不可能なものが存在します.これらを実現するために,量子コンピュータは量子世界の2つの基本的性質,重ね合わせと量子もつれを利用します.
ではここで,重ね合わせについて説明します.量子ビットは $|0⟩$状態(0ケットと読む),$|1⟩$状態(1ケットと読む),もしくはこれらの2つの線形結合(重ね合わせ)の状態をとり得ます.ハーフアングルブラケット記法は往来,通常のビットとは異なる量子ビットの状態を表すために用いられています.$|0⟩$状態を観測すれば古典ビットでの$0$と同等な情報が得られ,$|1⟩$状態を観測すれば古典ビットでの$1$と同等な情報が得られます.IBMを含む多くの量子計算の物理的実装において,$|0⟩$状態はエネルギーが最も低い状態であるため,この状態を基底状態と呼ぶこともあります.
つづいて,量子もつれについて説明します.量子もつれは多数の重ね合わせ状態が生み出す特性であり,古典物理学には存在しない概念です.もつれ状態では,たとえ持ちうる情報が完全でなくとも,そのシステム全体を明確に記述することができます.2つの絡み合った量子ビットのうちの1つを観測すると観測値はランダムに振る舞いますが,同様の方法で観測された場合,他の(観測していない)量子ビットがどのように動作するかを観測者に正確に伝えることが可能です.量子もつれには,2つの量子ビットの個々のランダムな振る舞いの間に相関が含まれるため,メッセージの送信に使用することはできません.一部の人々はこの現象を"instantaneous action at a distance"(距離のある瞬間的なアクション)と呼んでいますが,これは誤解です.アクションというよりはむしろ,相関があります.2つの量子ビットの観測結果間の相関は,観測値が比較される場合の2回の測定の後にのみ現れます.量子もつれ状態に存在する量子コンピュータの能力は,その強大な計算能力の他に,古典的には実行できない,または説明することができない多くの量子情報処理分野の功績に関与しています.
重ね合わせと量子もつれのより詳しい概念を学ぶには,俳優Paul RuddがQuantum Chessの試合でStephen Hawkingを倒すのを見ていただくのがよいでしょう.Quantum Chessのルールはオンラインで公開されており,このゲームの発明者Chris Cantwellとチェスの専門家Anna Rudolfの対戦を見ることができます.また,IBMのウェブサイトから,IBMフェローのCharlie Bennettの量子概念に関する基礎レベルと応用レベルのイントロダクションを読むこともできます.
あなたが量子概念の背景にある数学と理論をより深く理解したいなら,IBMのFull User Guideを読み進めることをお勧めします!
Getting Started -さあやってみよう-
Quantum Composerは量子プロセッサを操作するためのGUIです.これは測定値と量子ゲート(qubitsの状態を変化させる操作)の洗練されたライブラリを使用して量子アルゴリズムを構築するツールだと思ってください.
このガイドでは,さまざまな実験を試してみましょう(あなたが好きなものを気楽に試してみるとよいでしょう).Composerタブを最初にクリックすると,実験の名前と,実際の量子プロセッサまたはカスタム量子プロセッサ(シミュレータ)を実行するかを選択する画面が出てきます.カスタムを選択すると,実験での量子ビット数と古典ビットレジスタの古典ビット数が選択されます(量子ビットの数と同じにすることができます).実際のプロセッサでは,量子ビット間の接続は実験的な設定によって制限されます.実験上測定にいくつかの誤差も生じますが,カスタムプロセッサでは、量子ゲートはどこにでも配置することができます。実験的なエラーはありませんが,量子情報の性質によってランダムな結果が生じることがあります.このガイドでは,(実験誤差によって生じる偏差についての混乱を避けるため)カスタムプロセッサで実験を実行した結果を示します.違いを理解できるよう,カスタム量子プロセッサと実際の量子プロセッサの両方でいくつかの実験を実行することをお勧めします.
Composerは,スポーツの試合のようなスコアではなく,音楽的な意味での量子スコアを作成することができます.量子スコアは,音楽と同様に時間は左から右に向かって進みます.各行は量子ビット(時間とともに量子ビットに何が起こるか)を表します.各量子ビットは音符のように異なる周波数を持っています.量子アルゴリズム(回路)は,量子ビットを明確に定義された状態(例えば下の図で言う$|0⟩$)を用意することから始まります.そして左から右にかけて,一連の単一量子ゲートないし多量子ゲートを実行します.
量子ゲートは正方形のボックスで表され,異なる持続時間,振幅,および位相について周波数を操作します.これらは単一量子ゲートと呼ばれます.量子ビットにゲートを適用するには,ゲートボックスを量子ビット上にドラッグするだけです.削除するには、ボックスをダブルクリックするか,ごみ箱にドラッグします.
すべてのゲートと測定値を入力したら,"Run"(実際のプロセッサでのみ使用可能)または"Simulate"をクリックして実験結果を生成します.各回路は,実験を実行するために測定ゲートで終了する必要があります.
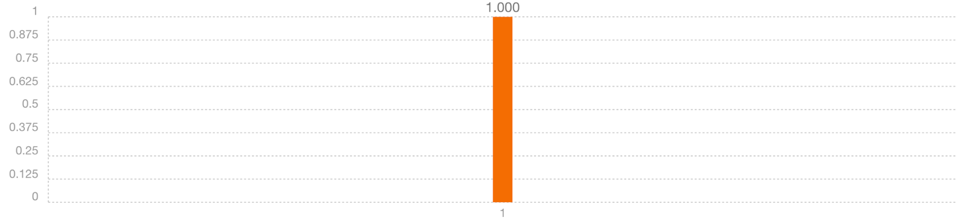
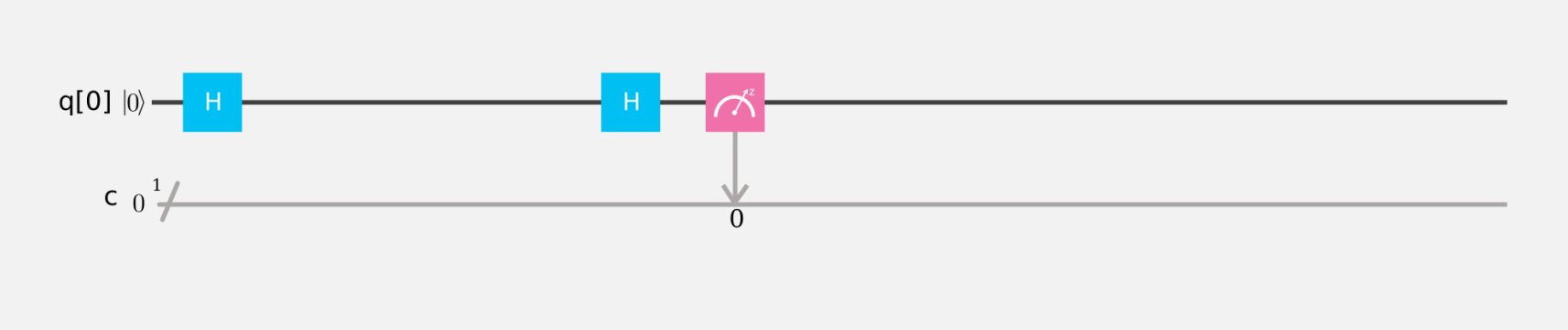
単一量子ビットの測定:
上記の例では,古典ビットレジスタに1つの古典ビットを持つ単一量子ビットのスコアを作成しました.具体的には,量子ビット$"0"$を測定し,測定結果を古典ビットレジスタの0番目の位置(スコアcの下の線)に記憶しました.
量子測定を実行した後,量子ビットの情報は古典ビットへ渡されます.これは重ね合わせおよび量子もつれの量子特性を失うことを意味します.測定値は$0$もしくは$1$です.$0$でなければ$1$だし,逆も然りです.
時には重ね合わせ状態にあるときのように,$|0⟩$と$|1⟩$の存在確率が等しい場合もあるでしょう.そのような場合,実際のデバイスで何度も実験を繰り返す(Simulateのプルダウンメニューの"shots"で実験回数を設定)と,$0$を測定する回数と$1$を測定する回数が半分ずつであることに気づくでしょう.
IBM Q Experienceでは,量子スコアの結果がヒストグラム/棒グラフ表示で表示されます.
Histogram representation (Bar graph) -ヒストグラム表現(棒グラフ)-
ヒストグラム/棒グラフ表示では,各バーの下部にある$0$と$1$の組み合わせは量子ビットの測定状態を表します.バーの高さは実験で行われたそれぞれの実行でどのくらいの頻度で測定結果が発生したかを表します.より多くの量子ビットを使用するほど,結果を表現するためには$0$と$1$の数が多くなります.スペースを節約するために,発生しなかった測定結果はヒストグラムから省略され,低周波な測定結果は"other values"とラベル付けされたバーに結合されることがあります.
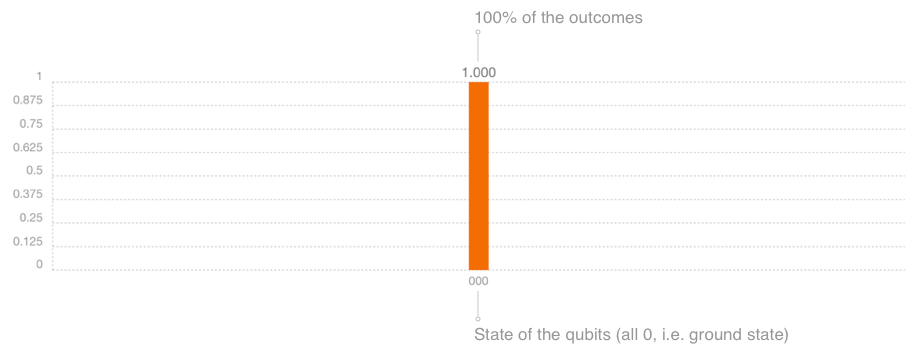
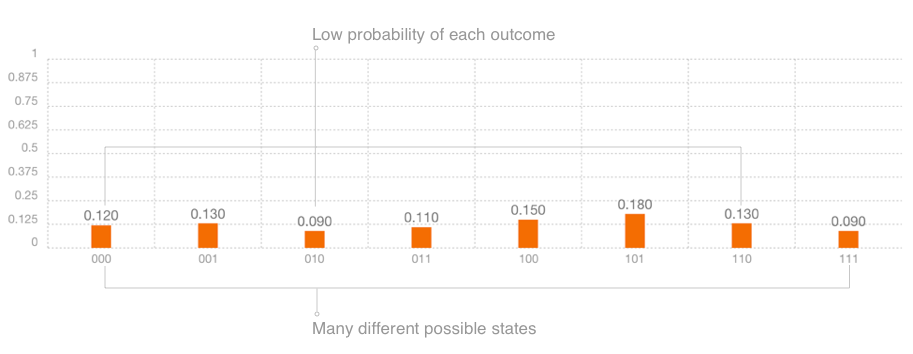
これを自分で試してみるには,Composerで3つの量子ビットで新しい実験を作ります.ピンク色の測定ゲートを各バーにドラッグして,"Run"または"Simulate"をクリックします.この時点では出現可能な結果は1つしかありません.$000$はすべての量子ビットが$|0⟩$の状態を指し,この場合私たちは量子ビットの持つ情報に一切変更を加えていません.次に,測定前に青色のHゲートを各量子ビットにドラッグします.Hゲートに適用された各量子ビットは,$0$と$1$の存在確率が等しい重ね合わせ状態になります.今度はもっと多くの測定結果が発生することが予期されます.Hゲートについては後のセクションで詳しく説明します.
3量子ビット測定:基底状態
この記事を読んだ方からコメントで,QuantumProgramクラスはQiskit0.6.0で削除されていると教えていただきました(リリースノートはこちら).そこで,,Qiskit0.6.0でも動作する,記載のサンプルコードと同じ回路が動くコードを自作しました.こちらであれば問題なく動作するかと思われます.ご活用ください↓.
Qiskit Terra 0.6.0 以降でも動作するコードはこちら
# use QISKit.org
from qiskit import QuantumProgram
# useful additional packages
from tools.visualization import plot_histogram
# Define the QProgram and the Quantum and Classical Registers
qp = QuantumProgram()
q = qp.create_quantum_register("q", 3)
c = qp.create_classical_register("c", 3)
# Define the circuit
threeQ = qp.create_circuit("threeQ", [q], [c])
threeQ.measure(q[0], c[0])
threeQ.measure(q[1], c[1])
threeQ.measure(q[2], c[2])
# Execute the circuit
result = qp.execute(["threeQ"])
# Plot result
plot_histogram(result.get_counts("threeQ"))
3量子ビット測定:完全な状態の重ね合わせ
Qiskit Terra 0.6.0 以降でも動作するコードはこちら
# use QISKit.org
from qiskit import QuantumProgram
# useful additional packages
from tools.visualization import plot_histogram
# Define the QProgram and the Quantum and Classical Registers
qp = QuantumProgram()
q = qp.create_quantum_register("q", 3)
c = qp.create_classical_register("c", 3)
# Define the circuit
threeQ = qp.create_circuit("threeQ", [q], [c])
threeQ.h(q[0])
threeQ.h(q[1])
threeQ.h(q[2])
threeQ.measure(q[0], c[0])
threeQ.measure(q[1], c[1])
threeQ.measure(q[2], c[2])
# Execute the circuit
result = qp.execute(["threeQ"])
# Plot result
plot_histogram(result.get_counts("threeQ"))
The Weird and Wonderful World of the Qubit -量子ビットの奇妙で素晴らしい世界-
量子ビットは$|0⟩$と$|1⟩$の2つのエネルギーレベルで構成されるシステムです.$|0⟩$状態は2つのエネルギーレベルのうち低い方であるため,基底状態と呼ばれることもあります.$|0⟩$と$|1⟩$を合わせると,「標準基底ベクトル」を作ることができます.ベクトルと同様に,それらは方向と大きさを持ちます.基底ベクトルを定義することは,線形代数から拝借したとても便利なトリックです.一度これらのベクトルを定義すれば,基底ベクトルの線形結合から他のベクトルを構築できるというのが基本的な考え方です.
さらに,量子ビットは「位相」をもちます.これは重ね合わせが複雑になることが原因です。これらの重なり具合を表現するために,基底状態の前に$a$や$b$のような係数を次のように入れます.
a|0⟩+ b|1⟩
この式の意味は次のようになります:"状態は$|0⟩$と$|1⟩$の線形結合で構成され,それぞれの状態の存在確率は係数$a$と$b$に依存する" 係数$a$と$b$は正負両方の値をとることが可能で,それ以上に複雑な値もとり得ます.$a$,$b$を二乗した値($|a|^2, |b|^2$)は,それぞれ$0$,$1$の結果を測定する確率になっています.
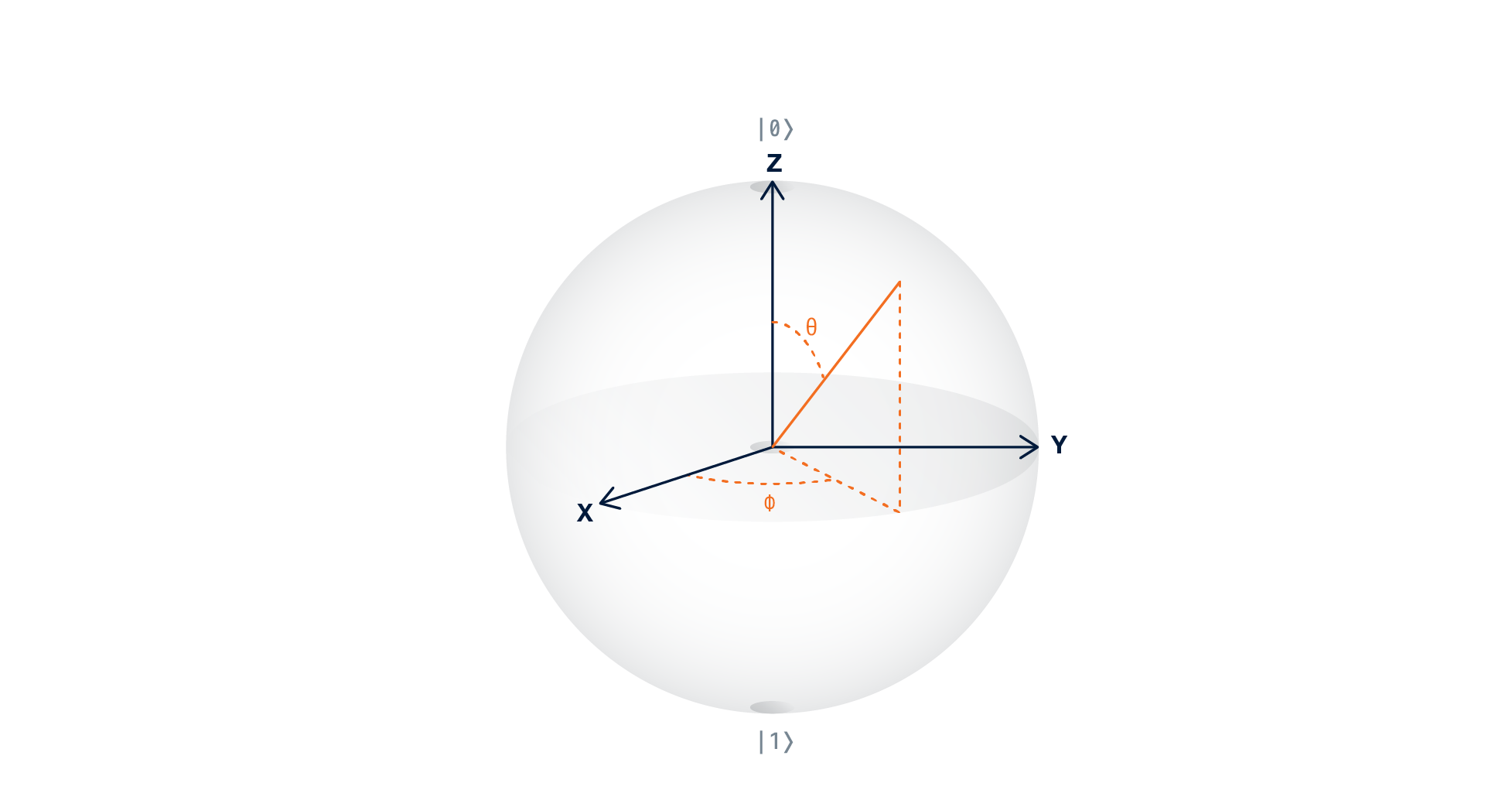
基底は$|0⟩$と$|1⟩$で表され,それらの線形結合$a|0⟩+b|1⟩$は単一量子ビットの状態を表します.係数$a$と$b$は実数に限らず,虚数や複素数もとり得るため,量子ビットを視覚化するには「ブロッホ球」と呼ばれる特別なツールが必要です.ブロッホ球は半径1の球であり,その表面上の点は量子ビットの状態を表します.地球の表面上の点を記述するために経度と緯度を使用するように,ブロッホ球は角度を使って量子ビットの状態を記述することができます.この表現は,複素係数を含む量子ビット状態をブロッホ球の表面上の点として表現することを可能にします.$X,Y,Z$軸に沿ったブロッホ球の表面上の点は,以下に説明する特別な状態に対応します.
量子ビットの状態は,上の画像のオレンジ色の線で示されています.この図では球の頂点の状態は$|0⟩$を表し,球の底の状態は$|1⟩$を表します.量子ビットが$|0⟩$と$|1⟩$の重ね合わせをとると,ブロッホベクトルは$|0⟩$と$|1⟩$の間のどこかを指します($θ$が$0$なら真上を指し,$π$なら真下を指します).
量子ビットは球面上にもう一つ自由度を持っています.$Z$軸周りの回転です.これは角度$φ$で表すことができます.$φ$の値は量子ビットの位相の変化を表しています.このブロッホ球の描写は,単一量子ビット表現でのみ機能します.図示の都合上,ブロッホベクトルの長さはブロッホ球の半径と等しいと仮定します.
Single-Qubit Gates -単一量子ゲート-
古典的なコンピュータが$0$もしくは$1$の状態を持つビットを操作し計算を行うように,私たちは量子コンピュータで計算を行うために量子ビットを操作します.このセクションでは,重要な単一量子ゲートを使用する方法を説明します.
これらが何を数学的に行うのかを理解するには,IBMのFull User Guideをチェックしてください.
X gate -Xゲート-
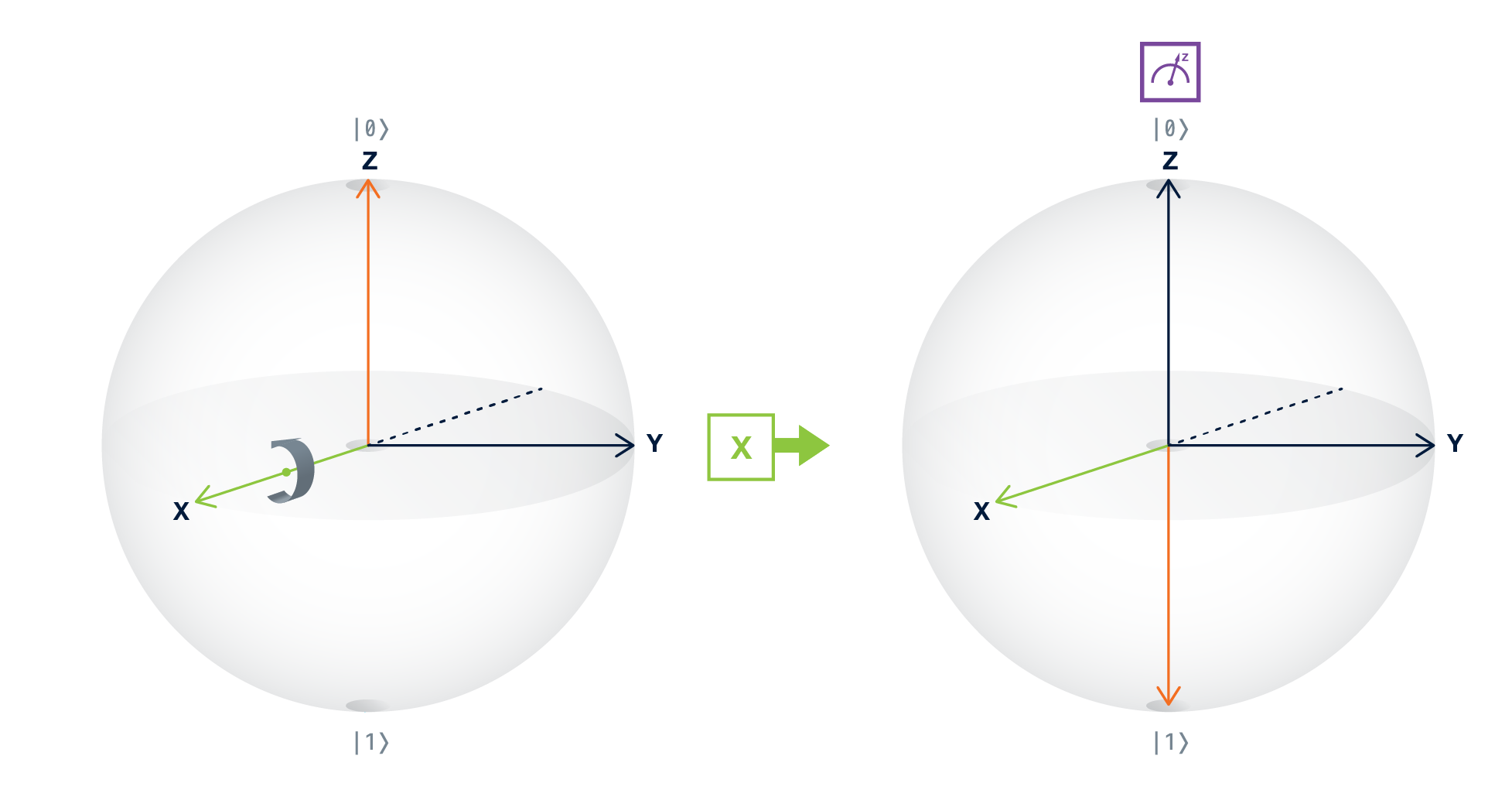
まずXゲートを使ってみましょう.Xゲートは$0$と$1$を反転させるので,ビット反転を行うゲートとして知られています.古典ゲートのNOTゲートに似ています.
このゲートはブロッホベクトルをX軸回りに$π$ラジアン回転させるため,X回転とも呼ばれます.もしブロッホ球の上部($|0⟩$)の状態でXゲートを適用すれば,ブロッホベクトルはブロッホ球の底($|1⟩$)に回転します.下の図を参考に,ComposerでXゲートを試してみてください.
Creating superposition -重ね合わせ状態をつくろう-
さて,ビット反転の次は,基底状態$|0⟩$と$|1⟩$の組み合わせである新しい量子状態を生成する重ね合わせについて見ていきましょう.
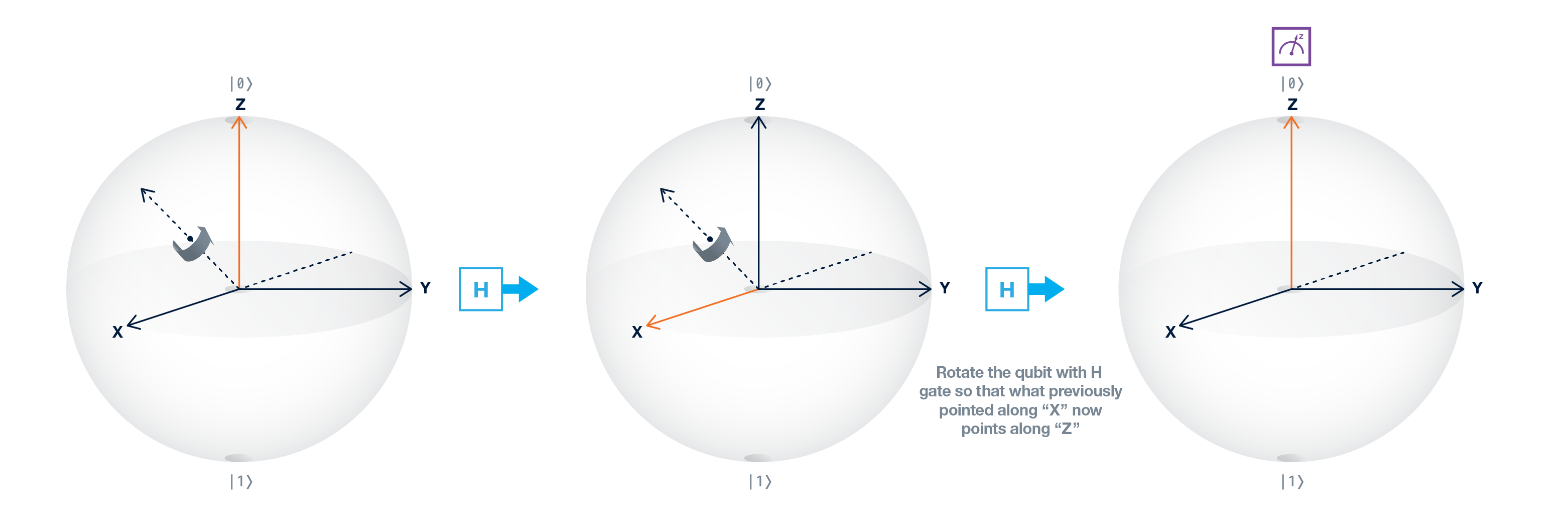
Hadamardゲートとして知られているHゲートを量子ビットの1つ(初期状態は$|0⟩$)に適用させ,観測を行います.量子ビットが実行回数の約半分回は状態$|0⟩$をとり,約半分回は状態$|1⟩$をとるはずです.測定が量子ビットの最終状態を選択させる前に,量子ビットの状態は$|0⟩$でも$|1⟩$でもない奇妙な状態にあります.これは$|0⟩$と$|1⟩$の2つの状態の組み合わせからなる等加重の重ね合わせ状態です.
Hゲートが$|0⟩$状態に適用される場合は特別に後述の記号と定義が存在します.
|+⟩=\frac{1}{\sqrt{2}}(|0⟩+|1⟩)
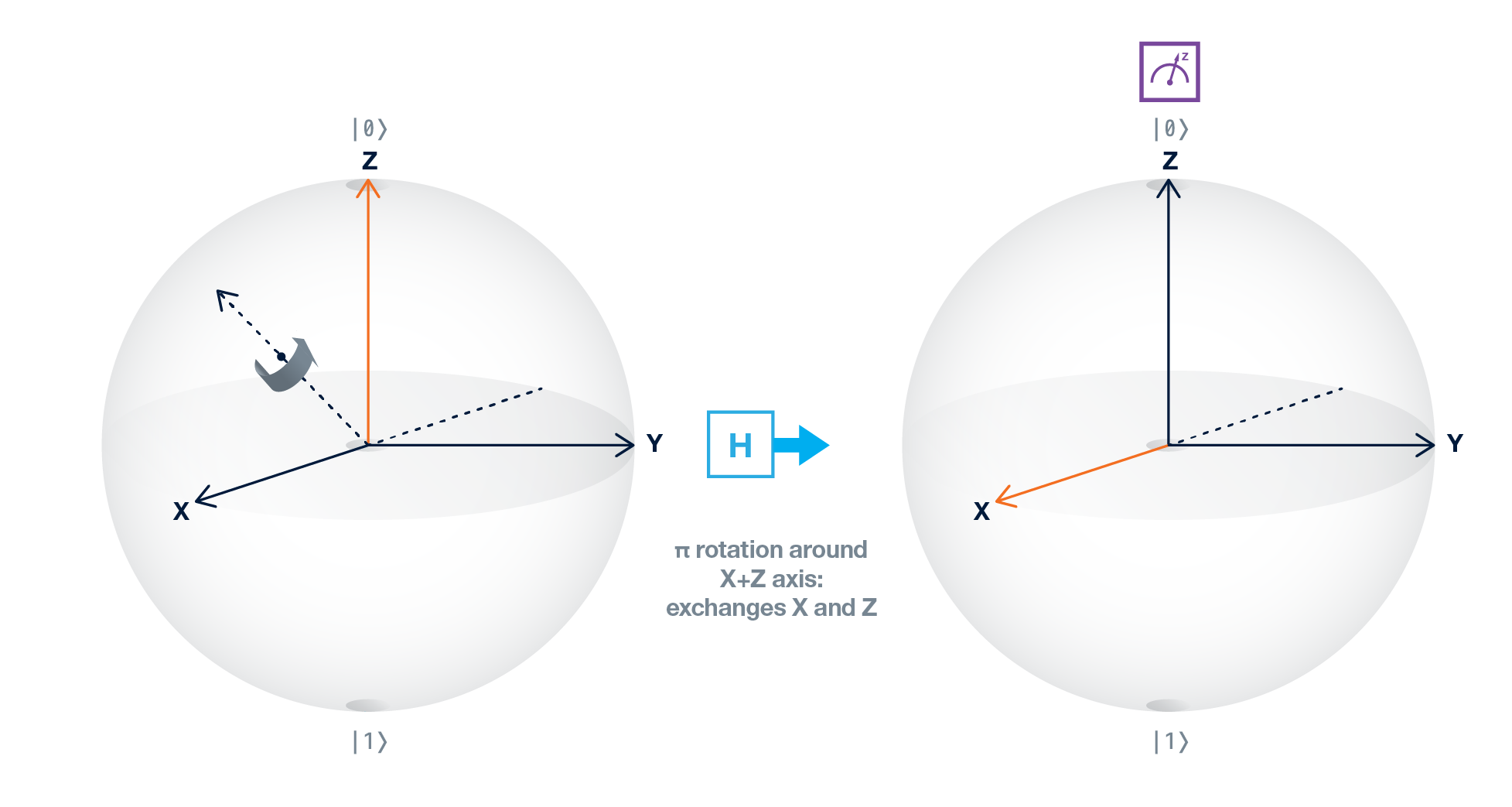
$|+⟩$は$|0⟩$が$1/2$の確率で観測され,$|1⟩$が$1/2$の確率で観測される特別な状態を表します(係数の二乗がその状態の存在確率になることを覚えていますか?) .Hゲートは(以下の図に点線で示したように)$X+Z$軸回りの回転として考えることができます.これは重ね合わせ状態の標準表現であり,ブロッホベクトルはブロッホ球上の$+X$を指します.
|+⟩重ね合わせ状態の標準表現:
上記の回路を100回実行した結果を示すヒストグラムの例を以下に示します. 平均してこの回路は等しい確率で0と1が得られると予想できますが,100回のコイントスで表が50回,裏が50回,という結果が一般的に得られないように,有限の試行回数でこの結果を正確に生成する可能性は低いです.
この状態も一緒に知っておきましょう.
|-⟩=\frac{1}{\sqrt{2}}(|0⟩-|1⟩)
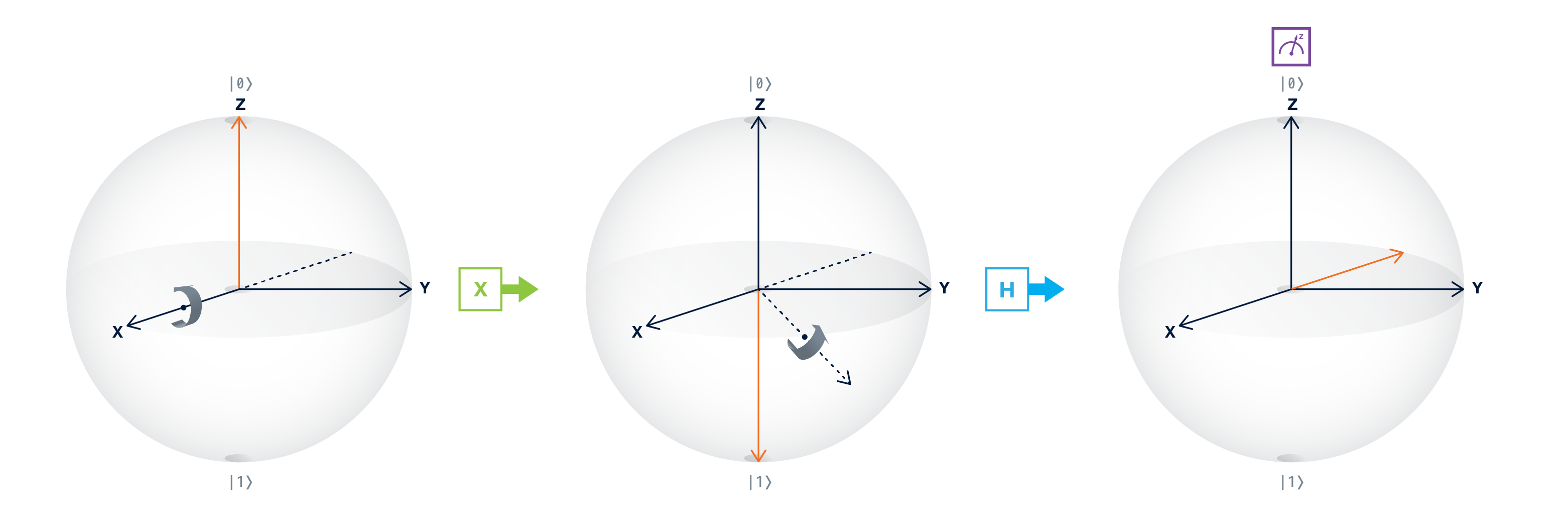
これはブロッホ球上で$-X$を指すベクトルであり,重ね合わせ基底と呼ばれる新しい基底(または測定方向)を定義できます.$|-⟩$状態は以下の回路を使用して作成されます.Xゲートで$|0⟩$を$|1⟩$に反転させ,次にHゲートで量子ビットを$X+Z$方向に回転させて$|-⟩$状態を生成します.この回路を実行すると,一つ前の実験と同様の結果が得られます.異なる状態が同じ結果をもたらしました!
$|-⟩$重ね合わせ状態:
$Z$方向(ピンク色の測定ゲートでアクセスできる唯一の方向)に沿って測定すると,量子ビットの位相に関する情報を得ることはできません.
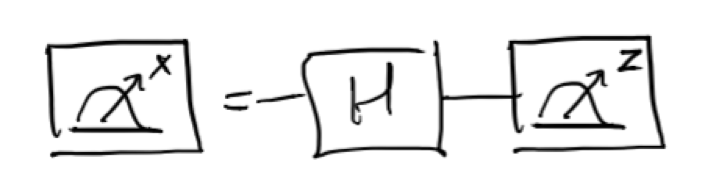
$|+⟩$と$|-⟩$の位相の違いを知るには,重ね合わせ基準で測定する必要があります.実験的には,ブロッホ球の異なる方向に沿って物理的に測定することはできません.標準測定($+Z$方向に沿ってのみ測定可能)を実行する前に,ゲートを使用して量子ビット状態を回転させることで測定値を変更したように見せることができます.$X$方向で測定するために,ブロッホベクトルの$X$成分が$+Z$方向に向くまで回転させます.これは測定前にHゲートを適用することによって実現されます.
$|+⟩X$方向で測定された状態:
$|-⟩X$方向で測定された状態:
上記の$X$方向で測定された$|+⟩$と$|-⟩$状態の測定を試し,その結果がそれぞれ$0$か$1$しか得られないことを確認してください.
この結果から,$Z$基準で測定すると観測結果は完全にランダムであることがわかります.しかし,X方向で観測される結果はフィクスト(ランダムでない)です!
Introducing qubit phase -量子ビットの位相について-
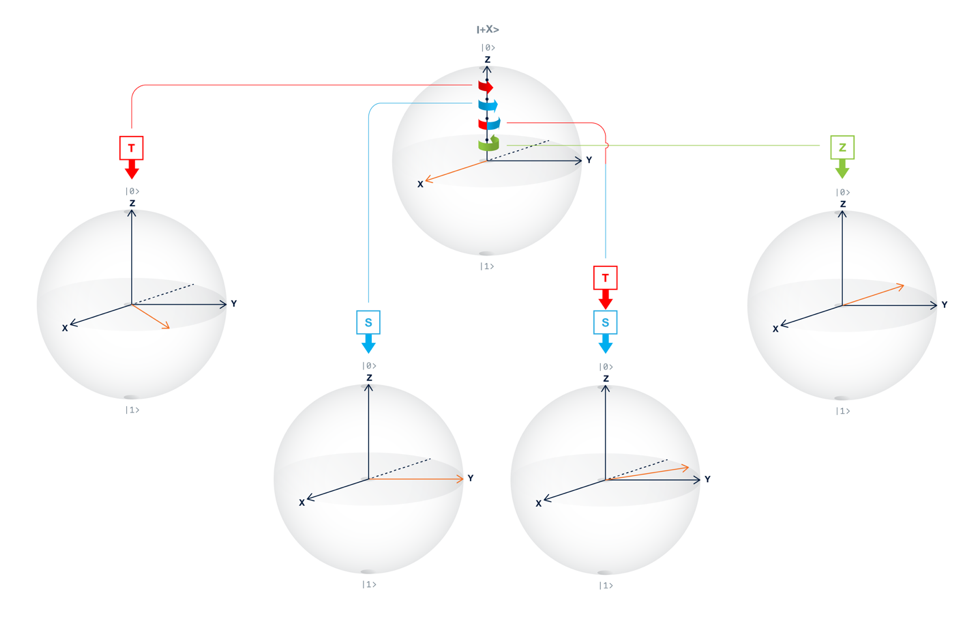
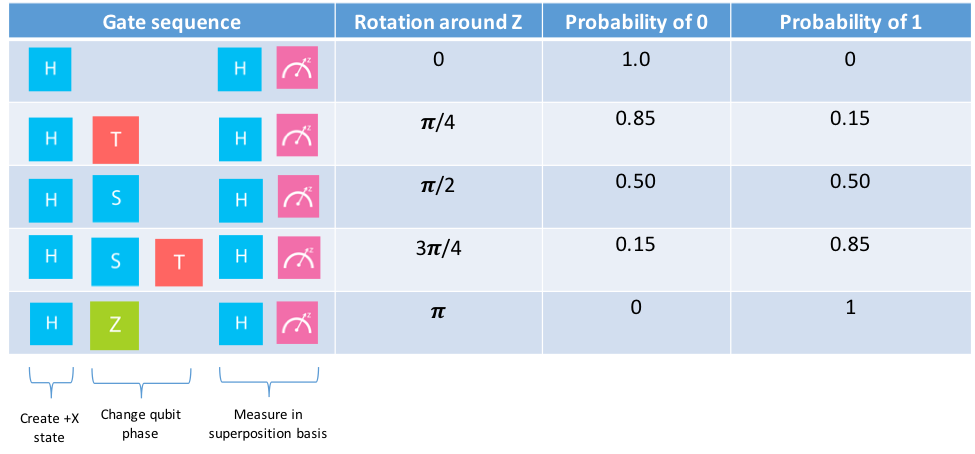
さて,私たちは既に$|0⟩$,$|1⟩$,そして重ね合わせ状態を作る術を学びました.次は,重ね合わせ状態の位相を変更する術を学びましょう.ここで,$Z,S,S^{†},T,T^{†}$ ゲートを追加します.
$Z$ゲートは$Z$軸の周りを$\pi$だけ回転させます.$S$ゲートは$Z$軸の周りを$\pi/2$,$T$ゲートは$Z$軸の周りを$\pi/4$だけ回転させます.$S^{†}$ゲートは$S$の逆元です.$S^{†}$は$Z$軸の周りを$-\pi/2$だけ回転させます($SS^{†}$は元の状態に戻ります).$T^{†}$ゲートも同様に,$T$の逆元を表しています.これらの回転は量子ビットの複素情報を表現しているブロッホ球の$Y$軸成分を与えます.
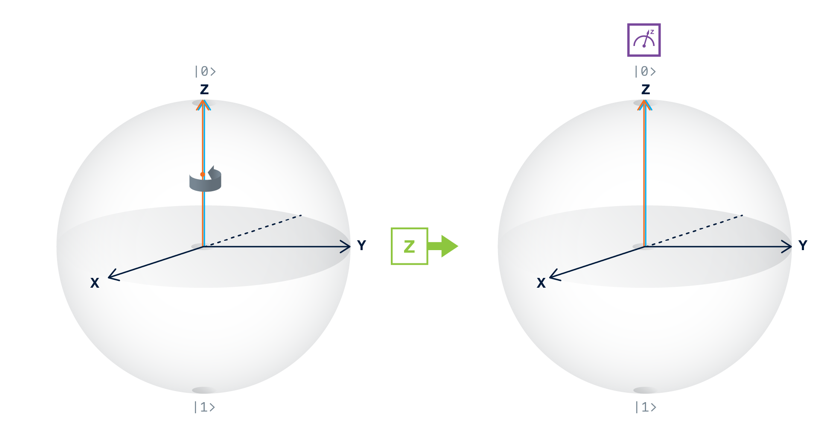
量子ビットが$|0⟩$状態にある場合$Z$は情報に影響を与えませんが,量子ビットが$|+⟩$状態にある場合$Z$が$|+⟩$から$|-⟩$に状態を反転させることが分かります.
Zゲート:量子ビットが$|0⟩$状態にある場合
次に,量子ビットが$|+⟩$状態にある場合の$Z$軸周りの回転を調べてみましょう.以下は量子ビットが重ね合わせ状態にある場合にZ軸周りの異なる回転が測定にどのように影響するかをまとめたものです.
Summary of quantum gates -量子ゲートまとめ-


Multi-Qubit Gates -多量子ゲート-
複数の量子ビットを持つマシンの状態の表記は,往来のコンピュータで使用されていたものと類似していますが,現在はケット($| ⟩$)の中に複数の数字を表記します.2量子ビットプロセッサの場合,量子ビットは$|00⟩,|01⟩,|10⟩$,および$|11⟩$の4つの状態になり得ます.左から右へ読むと,第1の数は第2の量子ビットの状態を表し,第2の数は第1の量子ビットの状態を表しています.つまり,最初の量子ビット(q0)は常に右端に表示されます.この表記法は古典的な2進表現と一致します.単一量子ビットのように,これらの状態の重ね合わせも可能です.
\frac{1}{\sqrt{2}}(|00⟩-|11⟩)
この状態が測定されると,両方の量子ビットからは同じ値が得られますが,50%は両方とも$0$をとり,50%は両方とも$1$をとります.
量子の世界でこれら多くの構成を利用するためには,量子ビット間の条件づけされた論理を実行するゲートが必要です.量子ビットの状態は別の量子ビットの状態に依存します.
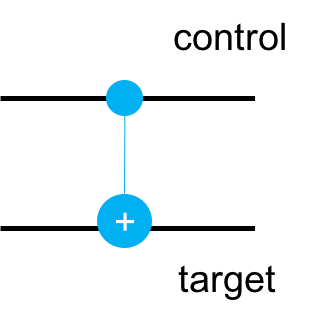
条件付きゲートはControlled-NOTまたはCNOTです.以下のように表されます.
CNOTゲートは制御(control)量子ビットが$|1⟩$である場合にのみ,標的(target)量子ビットを反転(NOTゲートまたはXゲートを適用)します.それ以外の場合は何も行いません.
2量子ビットにCNOTゲートを適用した場合,以下のように変化します(最初(右側)の量子ビットが制御量子ビットです).

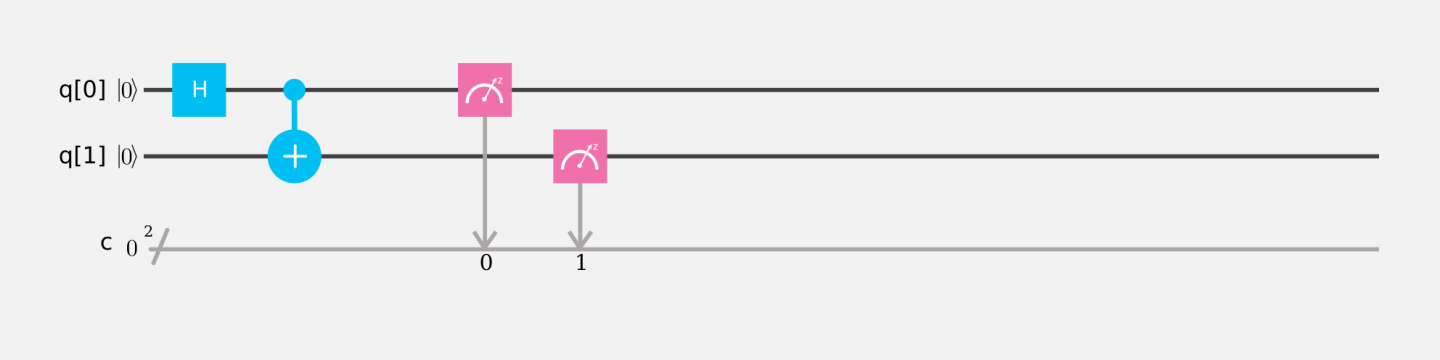
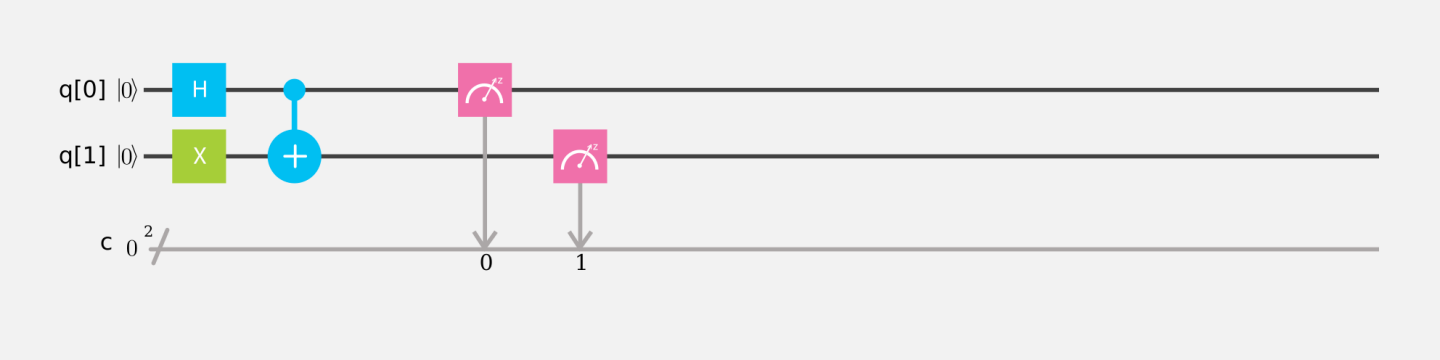
以下に示したCNOT回路の例を用いて,様々な入力状態を試してみてください.CNOTゲートを標的量子ビットにドラッグし,制御量子ビットをクリックしてそれらの間につながりを追加します.各回路のXゲートの構成が違う点に注意しましょう.
CNOT(入力$00$)
CNOT(入力$01$)
CNOT(入力$10$)
CNOT(入力$11$)
Entanglement -量子もつれ-
では,量子の世界において最も奇妙な現象,量子もつれについて見ていきましょう.2つ以上のもつれた量子は,その間に互いに影響を及ぼせないほどの距離があるにも関わらず,1)独立的にランダムであるだけでなく,2)あまりにも強く相関し,それぞれの量子が他の対象から独立していると考えることで説明がつきます.もつれ状態にある量子ビットは,重ね合わせ状態を分解してリスト(ある特定の状態をとっている1つ1つの量子ビットの集合)として表現することはできません.複数の量子ビットからなる一つの状態なのです.例えば,$|00⟩,|01⟩,|10⟩,|11⟩$の2つの量子ビット状態のいずれも,それぞれの量子ビットごとの状態を得ることができれば,他の全ての量子ビットの状態を記述することができるため,量子もつれ状態は発生しません.以下のような状態
\frac{1}{\sqrt{2}}(|00⟩+|01⟩)
もまた,第1の量子ビットが重なり合った単一量子ビット状態
\frac{1}{\sqrt{2}}(|0⟩+|1⟩)
にあり,第2の量子ビットが|0⟩状態にあると表現することができるため,量子もつれ状態は発生しません.しかし状態
\frac{1}{\sqrt{2}}(|01⟩+|10⟩)
は,1つの量子ビットの状態をリストとして表現する方法がないため,量子もつれ状態が発生します.もしもつれ状態にある量子ビットのうち,どれか一つを観測した場合,得られるランダムな観測値から,観測した量子ビットともつれ状態にある他の量子ビットが(測定軸が同様の場合に)どのように振る舞うかを完全に予測できます.
量子もつれ状態の例とBell状態の2つの例:
この概念を受け入れがたい人もいるでしょう.私たちの古典的な(本能的な?)直感としては,測定するまで2つの粒子が重なり合って存在するのではなく,1つの量子ビットはずっと$1$で,もう1つの量子ビットはずっと$0$であるように思いますよね.これは"local hidden variable"と呼ばれています.
Bell状態ともつれ状態の例:
Bell状態ともつれ状態の例(2):
Bell and GHZ Tests -BellとGHZのテスト-
この問題を最終的に解決するために,John BellはBellテストと呼ばれるテストを作成しました(後にCHSHの不等式に拡張されました).彼は,同じ軸(例えば、$Z$軸方向)に沿ったもつれ状態にある2つの量子ビットの両方を測定すると,常に相補的な値が得られましたが,これは古典的な説明(すなわち観測する前にその結果が事前に決定するような規則)を有することに気付きました. 代わりにBellは,異なる測定方向に沿って2つの量子ビットの測定を行い,結果の統計をとることによって,粒子が古典的に振舞っていないことを示すことに成功しました.これが2つの量子間でどのように機能するかを説明するには,統計学の知識が必要になるため,ここでは説明しません.代わりに,より高度な多量子ビットのもつれ状態を導入しましょう.
2つの量子ビットの代わりに3つの量子ビットを準備しましょう.次のような重ね合わせ状態を用意します.
\frac{1}{\sqrt{2}}(|000⟩-|111⟩)
この状態をGHZ状態といいます.GHZ状態は1997年に初めて調査されたGreenberger,Horne,Zeilingerにちなんで名付けられました.この状態の測定を行うことで,私たちが世界に抱いている「こうあるはずだ」という考えが間違っていることがわかります.
古典的には,量子(ここでは量子ビット)は測定されたときに$0$または$1$の2つの状態のうちのどちらか1つの状態にしかなり得ません.さらに,それらが古典的粒子である場合,その測定結果を事前に決定する"hidden variables"(隠れた変数)が存在します. GHZ状態の量子の性質を示すために,そしてhidden variablesが存在しないことを証明するためには,異なる軸($X$および$Y$)に沿った測定における出現可能な結果の異なる組み合わせ(相関)を考慮する必要があります.これは,1990年のN. David Merminの論文"What’s wrong with these elements of reality?"にて詳細に説明されています.
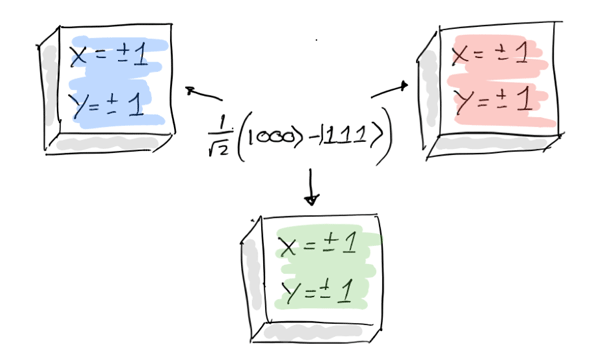
赤,緑,青の3つの独立したシステムについて,次の問題を解決しなければならないとします.それぞれのボックスに$X$と$Y$のラベルが付いた2つの問題が入っています.問題の答えは$1$か$-1$です.3つのシステムはGHZ状態の3つのもつれた量子ビットになり得ます.量子ビット間の相関関係を詳しく調べる必要がありそうですね.
この問題を解くために,$|0⟩$状態を$1$,$|1⟩$を$-1$と表します(これにより$0$の掛け算で情報を失うことを防ぎます).
量子ビットの各測定値は$1$または$-1$のいずれかになり,測地結果(つまり$1$か$-1$)を掛け合わせて相関を調べます.
実際にこのシステムがどう機能するのかを見てみましょう. 3つの量子ビットが$|000⟩$の状態にあるとしましょう.$Z$軸に沿って3つの量子ビットすべてを測定する場合,その測定値を$ZZZ$として表すとします.前述した書き換えの規則により,結果は$1,1,1$となり,$ZZZ$の値は$1$になります.状態が$|001⟩$の場合,$ZZZ$を測定すると$-1$が得られます.
$XXX$のような別の軸で測定するには,以前説明したように測定前にそれらを$Z$軸に回転させるために量子ゲートをに適用させる必要があります.$XXX$の場合,各量子ビットにHゲートを適用させなければなりません.3つの量子ビットについて以下のような測定を行った場合,次のような結果が得られます.
Bell and GHZ Tests (Cont.) -BellとGHZのテスト(続き)-
ここで,私たちの古典的な直感が間違いであることを示してみましょう.
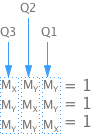
量子システムで量子測定を実行する代わりに,同様の古典的システムで古典的測定を実行するとします.この2つを区別するために,古典的なシステムでは$X$軸に沿って行われた観測での観測値を$M_{X}$,と記述します.$Y$軸に沿って行われた観測での観測値ならば$M_{Y}$と表します.
観測結果($M_{X}$または$M_{Y}$)が観測前に決定されていた場合,それぞれの量子ビットごとの測定値には$1$または$-1$が割り当てられています.上記はすべて3つの量子ビットの測定値を表しているので,個々の量子ビットごとに得られたであろう結果を得るために,掛け算をする必要があります(観測結果は観測より前に決定されていて,互いに独立であったことを確認しておきましょう!).
列の1つを掛けてみましょう.Q3は$M_{X}*M_{Y}*M_{Y}$となっています.これらの測定値は,$1$または$-1$のどちらかになることは既に分かっています.どちらの場合でも$M_{Y}*M_{Y}$は1になります.したがって,この式は単純化することができます.これをすべての列に対して行うと,上記の方程式系は$1$と等価であることが分かります.これは,この系が古典的である場合に得られる結果です.しかし量子力学と量子実験は,GHZ状態(古典的等価量子)における$XXX$測定の結果が$XXX=-1$であることを私たちに教えてくれます.
これらの実験の結果に基づいて,私たちは量子力学が教えてくれるこの奇妙な世界を受け入れなければなりません.独立した量子ビットの状態には,他の2つの量子ビットとは無関係に測定値$X$と$Y$の結果を事前に定めるhidden informationは存在しません.任意の量子ビットの$X$または$Y$測定の結果は,$X$とY両方の結果に基本的に依存しています.例えば,量子ビット2と3の$Y$測定値が$1$の場合,量子ビット1の$X$測定値は$1$になります.量子ビット2と3のX測定値が$1$の場合,量子ビット1の$X$測定値は$-1$になります.奇妙ですが,これは真実です!
重要なのは,3量子ビットシステム(例えば$XYY$の結果)の結合特性は予測することはできるが,各量子ビット(例えば$X,Y$)の個々の観測結果は予測できないということです.これは量子もつれ重要な特性です!
Results from the GHZ test in the Quantum Experience -量子実験におけるGHZ実験の結果-
私たちはIBM Q Experienceを利用することで,GHZ状態を作り,3つの量子ビットにゲートをかけてそれらを重ね合わせ,量子もつれ状態を実現し,上記の測定の組み合わせを実行することで,(驚くべきことに)自分でこのテストを行なうことができます.$X$軸に沿って3つすべてを測定すると,$Y$軸に沿った2つの量子ビットと$X$軸に沿った3つの量子ビットを測定する場合と比較すれば,この$"-1"$条件に相当するものが得られます.
この実験結果は,私たちのシステムが古典的な直感での予想でなく,量子力学に従って動作したことを示しています!

もう一度,確認しておきます.標準的な基準($Z$軸に沿う)を測定すると,$000$か$111$だけが得られます(丁度半分ずつ!).下の表のノイズ(小さな誤差)は,実際の(未だ不完全な)量子プロセッサーを使用したことによる実験的な誤差が原因です.
私たちはもうすぐこのBiginners GuideにIBM Q ExperienceでGHZテストを実装する方法についてのセクションを追加します!是非チェックしてください.
冒頭でも書きましたが,私は英語は決して得意ではないので,お粗末な和訳,文章が多々あるかと思います.量子計算分野もまだまだ勉強中の身です.よりよい文章にしていくため,ご意見ご感想頂けると幸いです.
長くなってしまいましたが,最後までご一読いただきありがとうございました.この記事があなたの学習の手助けになりますように.