面白い(?)ビット演算のせかい

　はじめに

　先日、私が通っている大学の文化祭がありました。情報学部の学生である私は、電子計算機研究会というサークルに所属しているのですが、そのサークルの文化祭の催し物としてLTをさせていただける機会があり、そちらで**「面白い(?)ビット演算のせかい」**というクソタイトルでLTをしたので、折角ですから記事にしてみました。一部分のスライドは省略（私の個人情報に関わる部分等）してあり、一部分についてはより詳細な内容を載せています。pythonによるプログラミングでの実行も載せてあります。（python2.7）

　ビットとは

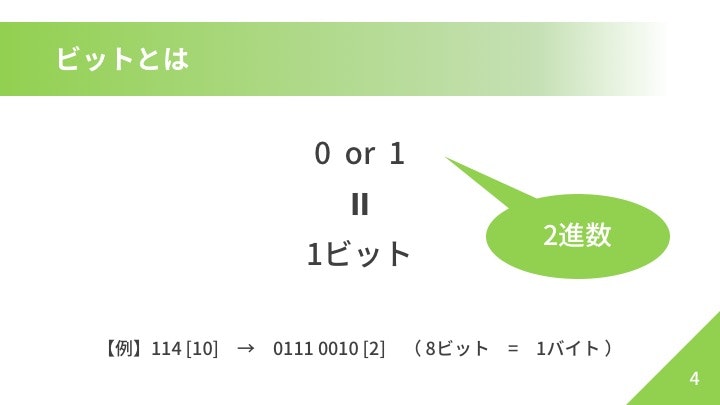
10進数から2進数へ変換方法は、色々と調べてみてください。（筆算での除算が一番有名？）
＊ 発表当日が11/4だっただけです。そっち系ではないです。

　ビット演算

ビット操作に関しては、上2つの方法で大体が落ち着くかと思います。

　ビット演算子

上の4つがよく使うやつだと思います。ANDやORにNOTをかけたNANDやNORもあります。ハード的にはよく使います。pythonでの実行例も載せておきます。formatは表示形式（0埋めなど）をわかりやすいように変えているだけなので、特にビット演算自体には関係はありません。

bit.py

a = 0b0111                      # 01 11
b = 0b0010                      # 00 10

print('{:#006b}'.format(-~a))   # 10 00 
print('{:#006b}'.format(a & b)) # 00 10
print('{:#006b}'.format(a | b)) # 01 11
print('{:#006b}'.format(a ^ b)) # 01 01

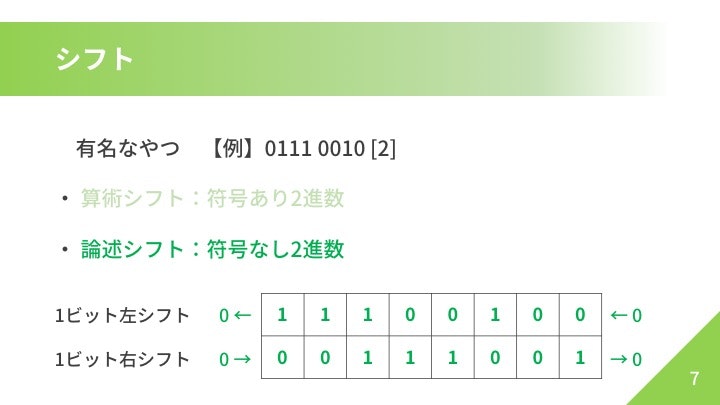
　シフト

・「論述シフト」ではなく「論理シフト」でした。すみません

今回の内容においては、論理シフトが重要です。算術シフトは、頭の1ビットを正負かどうかの判定に用いることで、負の数も表しちゃおうぜという人向けです。左シフトは**「<<」**、右シフトは**「>>」**となります。

bit.py

ab = 0b01110010                   # 01 11 00 10

print('{:#010b}'.format(ab << 1)) # 11 10 01 00
print('{:#010b}'.format(ab >> 1)) # 00 11 10 01

　ポップカウント

ここでは、2ビットずつから8ビットずつへ順に合算していきます。演算子とシフトでは、シフトの方が優先順位が高いことに注意です。

bit.py

ab = 0b01110010                          # 01 11 00 10

# 2ビットずつ
ab_1 = (ab & 0b01010101)                 # 01 01 00 00
ab_2 = (ab & 0b10101010) >> 1            # 00 01 00 01
print('{:#010b}'.format(ab_1 + ab_2))    # 01 10 00 01 : 2ビットずつ合算

# 4ビットずつ
ab_3 = ((ab_1 + ab_2) & 0b00110011)      # 00 10 00 01
ab_4 = ((ab_1 + ab_2) & 0b11001100) >> 2 # 00 01 00 00
print('{:#010b}'.format(ab_3 + ab_4))    # 00 11 00 01 : 4ビットずつ合算

# 8ビットずつ
ab_5 = ((ab_3 + ab_4) & 0b00001111)      # 00 00 00 01
ab_6 = ((ab_3 + ab_4) & 0b11110000) >> 4 # 00 00 00 11
print('{:#010b}'.format(ab_5 + ab_6))    # 00 00 01 00 : 8ビットずつ合算

　ハミング距離

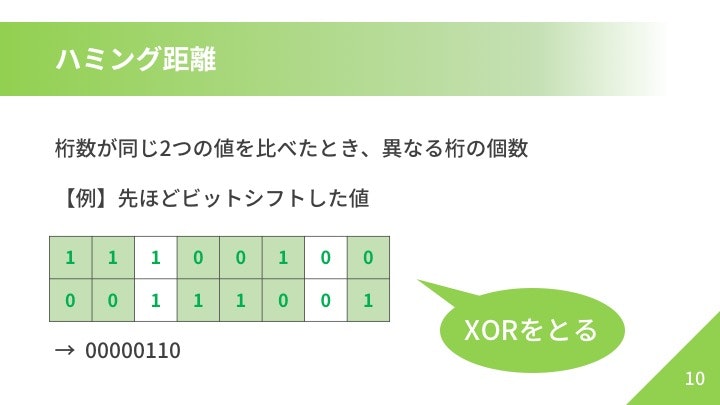
2つのビット列のXOR（排他的論理和）をとったあと、ポップカウントで"1"の個数を数えることができます。

bit.py

ab = 0b01110010
ab_xor = (ab << 1) ^ (ab >> 1)

ab_xor_1 = (ab_xor & 0b01010101)
ab_xor_2 = (ab_xor & 0b10101010) >> 1
ab_xor_3 = ((ab_xor_1 + ab_xor_2) & 0b00110011)
ab_xor_4 = ((ab_xor_1 + ab_xor_2) & 0b11001100) >> 2
ab_xor_5 = ((ab_xor_3 + ab_xor_4) & 0b00001111)
ab_xor_6 = ((ab_xor_3 + ab_xor_4) & 0b11110000) >> 4
print('{:#010b}'.format(ab_xor_5 + ab_xor_6))        # distance

# (ab << 1) -> 11 10 01 00
# (ab >> 1) -> 00 11 10 01 
#    ab_xor -> 11 01 11 01
#  distance -> 00 00 01 10

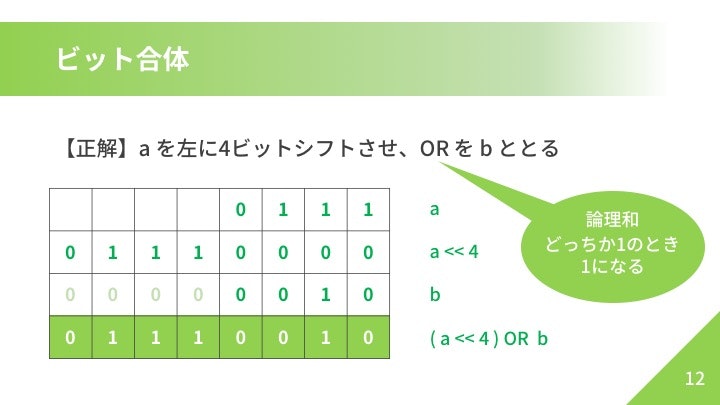
　ビット合体

使う頻度が高いビット合体。合体より連結の方がしっくりくるけど、面倒なので改名しません。

bit.py

a = 0b0111
b = 0b0010

print('{:#010b}'.format(a << 4 | b))

　まとめ

　とりあえず少ない時間と限られた中で発表できたのはこれくらいでした。もしかしたら今後追加するかもしれません？？もっと面白いものがあったらコメントで教えていただけると嬉しいです。