はじめに
Transformerでは活性化関数として$Gelu$が使われる。一方、一時期において脚光を浴びた$Mish$は一般的な単純な深い層のCNNでは精度の改善に効果があったが、NLPとかのTransformerでは精度改善が見られなかった。
ここで自分は入力データの分布が原因なのかもしれないと思った。つまり、画像データの入力は一様分布に近い。一方、自然言語処理の入力は$embedding$によって操作せずとも正規分布(ガウス分布)になっている。
従ってモデル各層において正規分布=>…=>正規分布とする分には基本的には$Gelu$が最も有利であり、一様分布=>…=>正規分布となっている場合のみ$Mish$が限定的に有利なのではないかと考えた。
さて、ここで一様分布に何か関数を掛けた場合に結果が正規分布となるためにはどんな関数を掛ければよいか考えてみる。
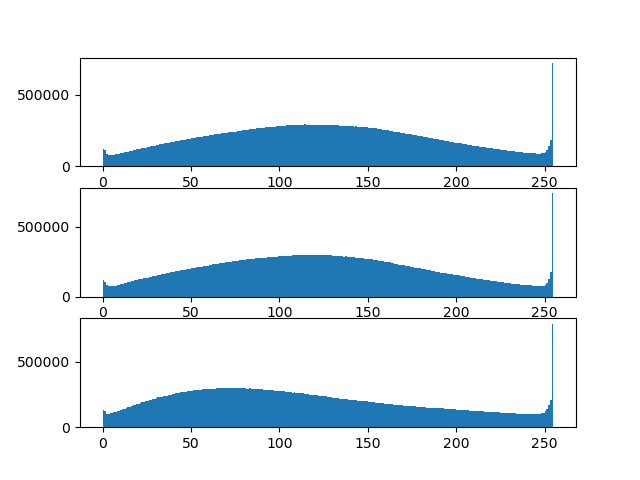
CIFAR-10の分布
その前にCIFAR-10の分布を一度確認しておく。結果は以下の様な分布になるが正規分布よりは一様分布の方が近く見える。$BatchNormalization$などの正則化ではこれをバイアスを足して分散で割って正規分布に近づけるが、それは平均と偏差を調整しているだけで正確な正規分布に変換できるわけではない。
分布でいえば単なる平行移動と拡大縮小をするだけである。
from tensorflow.python.keras.datasets import cifar10
import matplotlib.pyplot as plt
(x_train,y_train),(x_test,y_test) = cifar10.load_data()
x_train = x_train.reshape(-1,3)
fig = plt.figure()
ax1 = fig.add_subplot(3, 1, 1)
ax2 = fig.add_subplot(3, 1, 2)
ax3 = fig.add_subplot(3, 1, 3)
ax1.hist(x_train[:,0], bins=255)
ax2.hist(x_train[:,1], bins=255)
ax3.hist(x_train[:,2], bins=255)
plt.show()
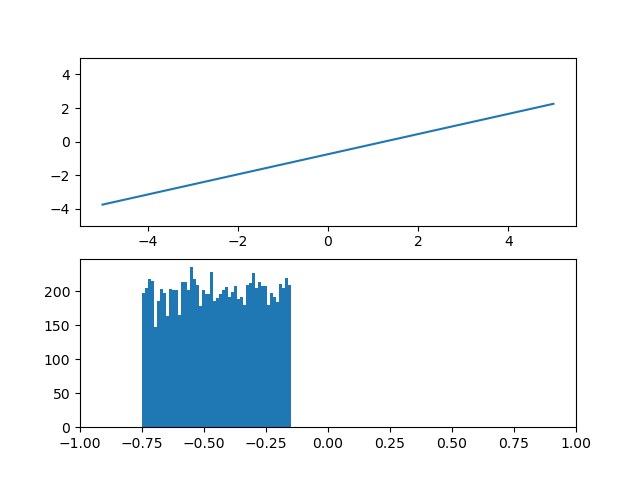
1. y=xの場合 (恒等関数)
考えるまでもない事だが変換関数が恒等関数なら入力が一様分布なら出力も一様分布のはずである。
最初の入力分布を0~1の一様分布とすれば変換関数と出力分布は以下の様になる。
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x
x1 = np.linspace(-5, 5, 1000)
y1 = func(x1)
x2 = np.random.rand(10000)
y2 = func(x2)
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(x1, y1)
ax1.set_ylim(-5, 5)
ax2.hist(y2, bins=50)
ax2.set_xlim(-1, 1)
plt.show()
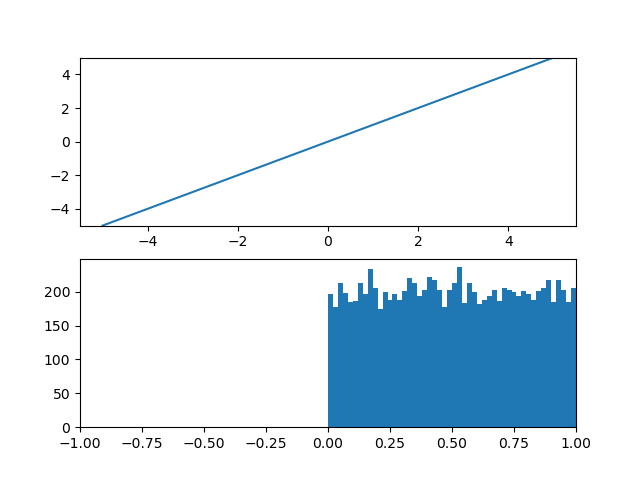
2. y=ax+bの場合
次に変換関数に傾きと切片を与えると一様分布は平行移動と拡大縮小が許される。
しかし、正規分布になるような形状の変化はない。
def func(x):
return 0.6 * x - 0.75
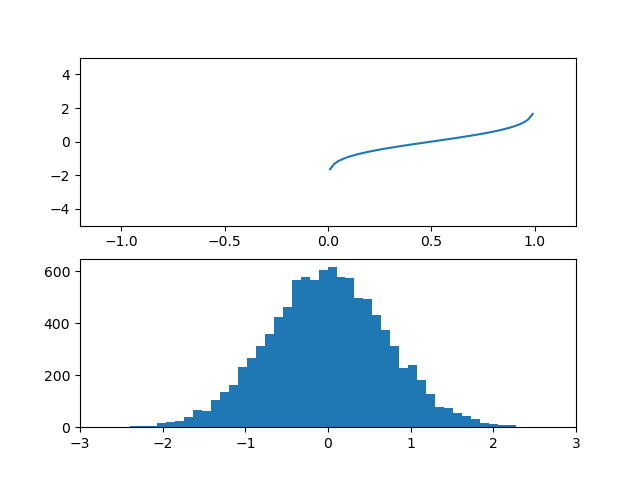
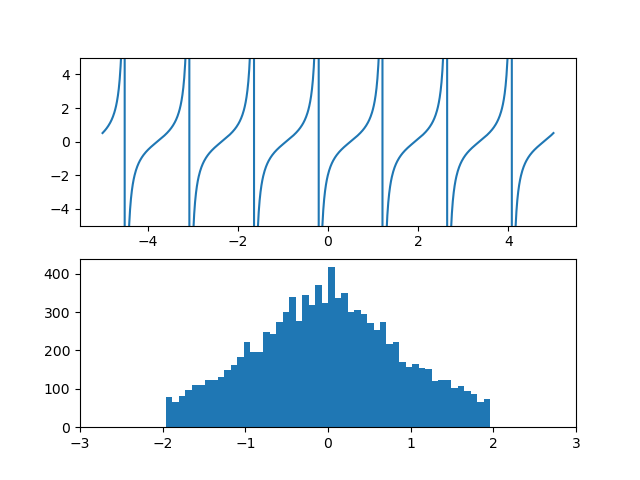
3. y=tan(x)の場合
一様分布が0~1の範囲だから変換関数はこの範囲でyは-∞~∞の変化をさせてみたい。
ただし、yの変化を-∞~∞とするとヒストグラムのグラフが上手く描写出来ないので0.7を掛けるトリックを加えた。この時、入力の一様分布は変換関数によって正規分布風に変化している。
def func(x):
return np.tan(np.pi * 0.7 * (x - 0.5))
この時、生成される分布は$\nu=1$のt分布(ローレンツ分布)に近いものが生成されるのではと推定される。
4. シグモイド型関数の逆関数
シグモイド型といえば標準シグモイド関数$\sigma(x)=\frac{1}{1+e^{-x}}$が有名だが、広義には0~1の変化をするς型の関数のことは全部シグモイド関数という。
さてここでシグモイド型関数の一種である以下の関数を考える。これは$\nu=2$のt分布の累積分布関数である。
y=\frac{1}{2}(1+\frac{x}{\sqrt{1+x^2}})
さて、これの逆関数を$y$に対して整理すれば
x=\frac{1}{2}(1+\frac{y}{\sqrt{1+y^2}})\\
(2x-1)^2=1-\frac{1}{1+y^2}\\
1+y^2 =\frac{1}{1-(2x-1)^2}\\
y=±\sqrt{\frac{1}{1-(2x-1)^2}-1}
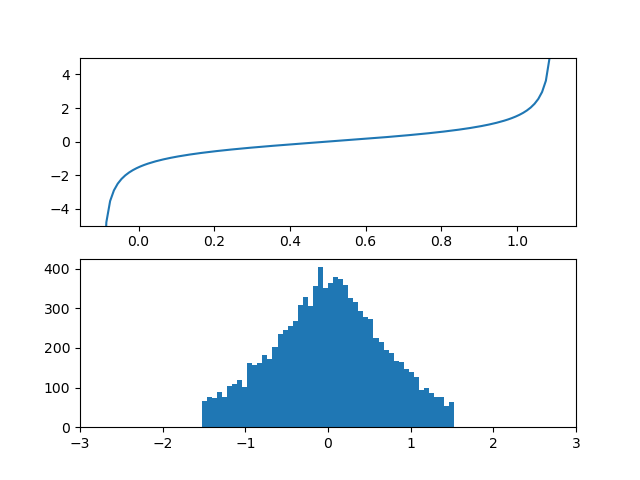
発散しないように0.7を掛けて変換関数を$(x-0.5)$の正負で場合分けする。
def func(x):
return np.where(x > 0.5, np.sqrt(1/(1-0.7*(2*x-1)*(2*x-1)) - 1),
-np.sqrt(1/(1-0.7*(2*x-1)*(2*x-1)) - 1))
この時、生成される分布は$\nu=2$のt分布に近いものが生成されるのではと推定される。
5. 正規分布累積分布関数の逆関数
さて本題である。3.と4.で変換関数としてシグモイド型関数の逆関数を選べば、一様分布を正規分布風に変換できることを示した。もっと言えば正規分布の逆累積分布関数を変換関数とすればぴったし正規分布に変換できるはずである。
従って変換関数は$erf(x)$関数の逆関数の時、理論上正規分布に変換できるはずである。
from scipy import special
def func(x):
return special.erfinv(1.0*(2*x-1))
※追記
あとで調べたところこの変換はRankGaussと呼ばれる処理に近い。誤差関数の逆関数も出てくる。
ただし、その手順はデータの大きさ順にソートして順位をラベル付けし、その順位の一様分布を強引に正規分布に変換するという手順だから元の値が偏っているなら必ずしも良い変換にはならない。
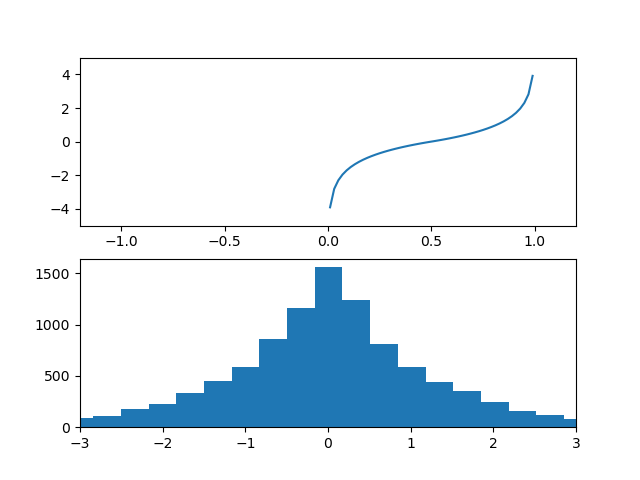
6. y=log(1+|x|)
例えば入力に画像の位置座標を与えたとすればその入力は等間隔なので一様分布である。
この一様分布にlog関数を与えた分布を確認する。
def func(x):
return np.where(x>0.5, -np.log(1+(1-2*x)), np.log(1-(1-2*x)))
特に正規分布には見えない。
何故こんなのを検討したのかというとSwin Transformer V2でLog-CPBというlog-spacedな座標があったので検討してみたがこの方針では正規分布に変換する関数には見えない。
参考:
Swin Transformer V2でのLog-CPB
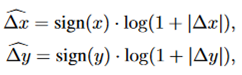
まとめ
入力が正規分布なら結局$Mish$よりも$Gelu$の方が優れているのではと考えた。
つまりNLPにおける$embedding$のように、画像の入力も正規分布にされていると良い。
この時、入力が一様分布なら変換関数を考えれば一様分布を正規分布に変換できる。幾つか変換関数を考えてみたが、その変換関数は誤差関数の逆関数であると思われる。
Log-CPBもその変換関数の一種なのかもしれない。