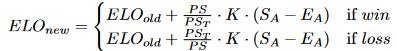はじめに
一般に5vs5のチーム戦を行う場合、単純なゲームではなければプレイヤーには決まった役職がある。このチーム戦における勝利貢献度はゲームにおける役職によって異なり、例えばあるゲームにおいてはヒーラーやサポートの勝利貢献度が低かったりする。このような場合、初心者や上級者をあえてその勝利貢献度の低い役職に割り当てることで、勝敗への影響を出にくくしてチームバランスを改善する。
イロレーティングにおいては一般にこのような役職重みを考慮することは無い。(そもそもチーム戦を考える事もしない)
Trueskillにおいてはこの役職重みは与えられた重みであれば考慮できるが、重みが不明の場合それを推定するのは困難である。
この記事内では役職重みを与えたイロレーティングについて考えてみたい。
前回記事
役職重みの推定
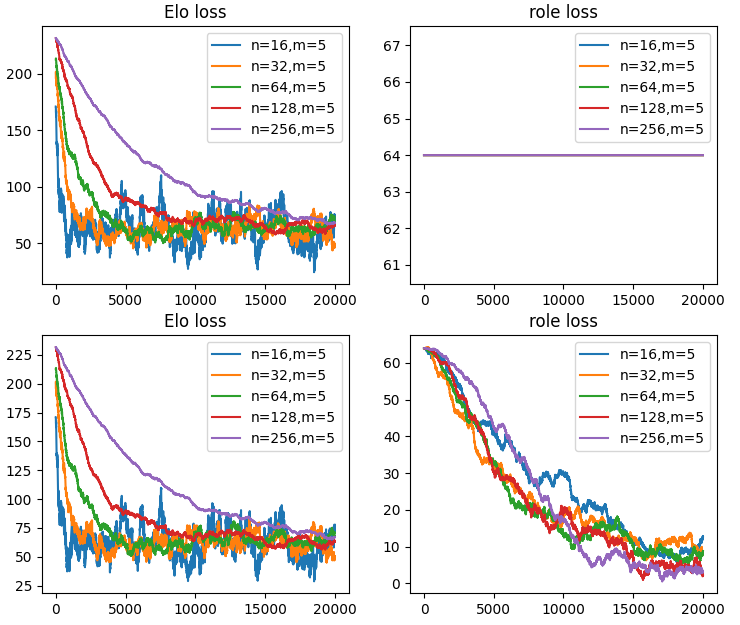
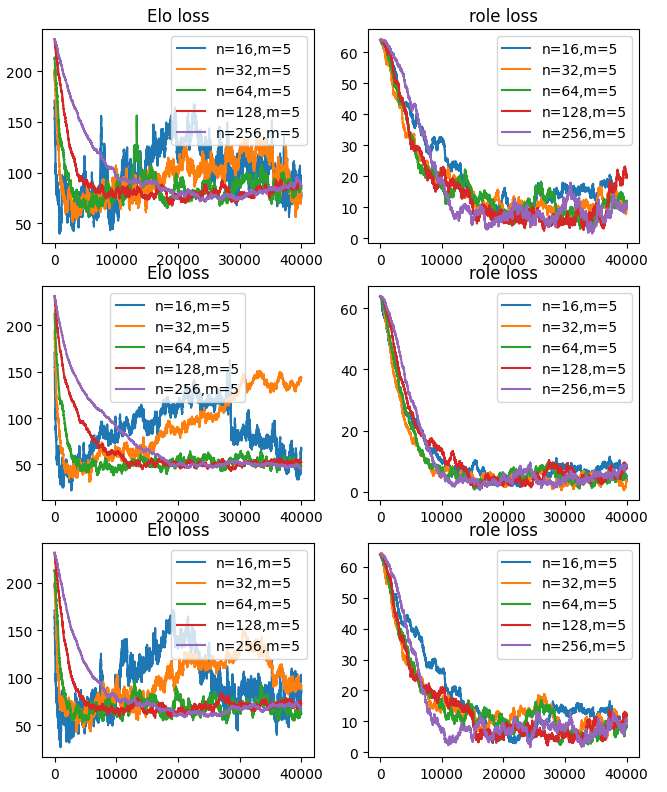
5vs5のランダムマッチングを考え、総和が1.0になるような役職重みを定義する。role_true = np.array([0.29, 0.26, 0.21, 0.14, 0.10])
role_predを均等な0.20で始め、チームのレートをA_score_true, A_score_pred = np.sum(Elo_true[A_team]*role_true), np.sum(Elo_pred[A_team]*role_pred)で求まるとして、勝敗結果からrole_predを適当に更新する。
更新項をrole_pred += (Elo_pred[A_team]-Elo_pred[B_team])/1500*(s-W_AB_pred)*0.002としてやると役職重みは正しい値に収束する。
import numpy as np
import matplotlib.pyplot as plt
import random
a = np.log(10)
fig = plt.figure()
ax = []
for index, m in enumerate([5,5]):
K = 32/np.sqrt(m)
ax.append(fig.add_subplot(2, 2, 2*index+1))
ax.append(fig.add_subplot(2, 2, 2*index+2))
for n in [16, 32, 64, 128, 256]:
seed = 100
np.random.seed(seed=seed)
random.seed(seed)
print(n,m)
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_true = Elo_true - (np.mean(Elo_true) - 1500)
Elo_pred = np.ones(n) * 1500
role_true = np.array([0.29, 0.26, 0.21, 0.14, 0.10])
role_pred = np.array([0.20, 0.20, 0.20, 0.20, 0.20])
l = list(range(n))
loss = []
loss2 = []
for t in range(20000):
sample = random.sample(l, 2*m)
A_team, B_team = sample[:m], sample[m:]
A_score_true, A_score_pred = np.sum(Elo_true[A_team]*role_true), np.sum(Elo_pred[A_team]*role_pred)
B_score_true, B_score_pred = np.sum(Elo_true[B_team]*role_true), np.sum(Elo_pred[B_team]*role_pred)
R_AB_true = A_score_true - B_score_true
R_AB_pred = A_score_pred - B_score_pred
W_AB_true = 1/(1+np.exp(-a*R_AB_true/400))
W_AB_pred = 1/(1+np.exp(-a*R_AB_pred/400))
s = 1 if W_AB_true > np.random.rand() else 0
Elo_pred[A_team] += K * (s - W_AB_pred)
Elo_pred[B_team] -= K * (s - W_AB_pred)
if index==1:
role_pred += (Elo_pred[A_team]-Elo_pred[B_team])/1500*(s-W_AB_pred)*0.002
role_pred -= (np.sum(role_pred) - 1.0)/5
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
loss2.append(np.mean(np.abs(role_true-role_pred))*1000)
print(Elo_true[:8])
print(Elo_pred[:8])
print(role_true, role_pred)
ax[2*index].plot(range(len(loss)), loss, label='n=%d,m=%d'% (n,m))
ax[2*index].set_title('Elo loss')
ax[2*index].legend()
ax[2*index+1].plot(range(len(loss2)), loss2, label='n=%d,m=%d'% (n,m))
ax[2*index+1].set_title('role loss')
ax[2*index+1].legend()
plt.show()
-------------------------------------
...
256 5
[1018.13706191 1609.97012929 1839.17324848 1441.64578121 1790.60490769
1658.48852641 1575.60453209 1210.39151642]
[ 970.31660623 1625.80232077 1868.80588784 1406.7334939 1710.58474707
1680.91085362 1518.35995047 1215.81593758]
[0.29 0.26 0.21 0.14 0.1 ] [0.28999601 0.26576633 0.20182979 0.14164333 0.10076454]
役職の得意不得意の推定
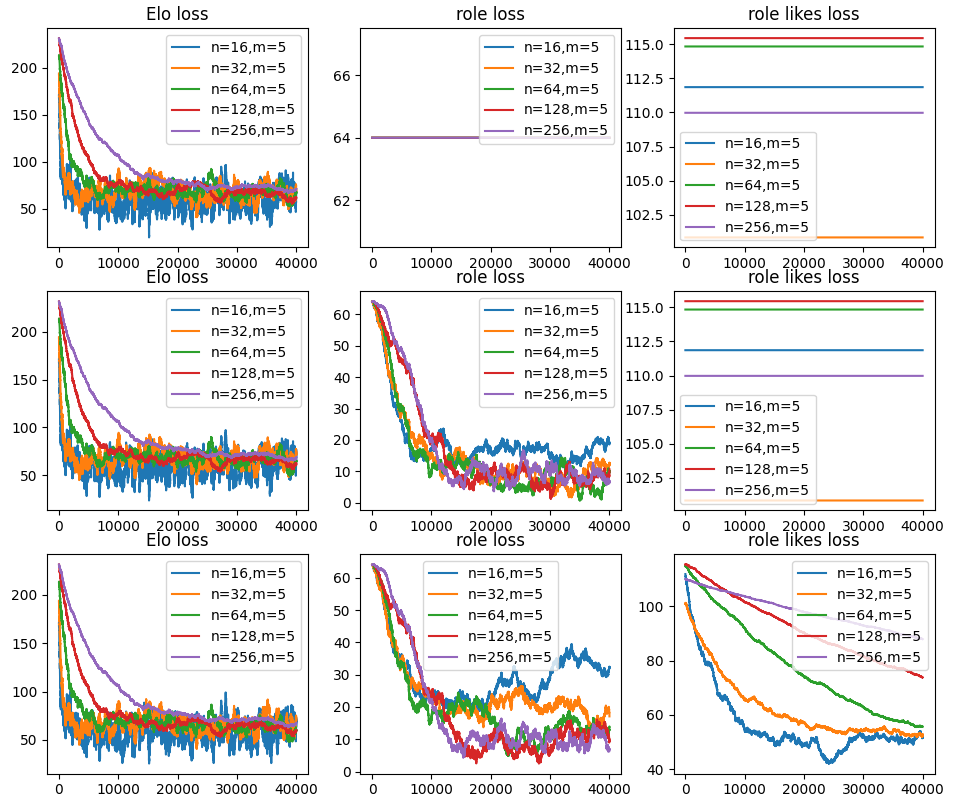
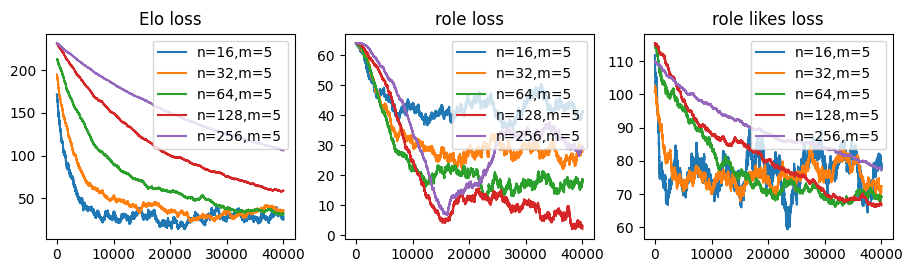
とはいえプレイヤーはどんな役職だって得意だというわけではなく、プレイヤーの役職にも好みがあるだろう。適当にrole_likes_true = np.random.randn(5,n) * 150で定義し、これに近づけるようにrole_likes_predを更新させてみる。
しかし、役職の得意不得意を学習させると、少人数において役職重みの最終到達損失は悪化してしまう。やった限りでは少人数ほど役職重みの損失が増えるので非常に多いプレイヤー数でないと役職の得意不得意は上手く学習出来ない。
また、役職の得意不得意の収束はEloの収束よりもかなり遅い。とはいえ更新量を増加させると役職重みの損失増大に繋がってしまう。
import numpy as np
import matplotlib.pyplot as plt
import random
a = np.log(10)
fig = plt.figure()
ax = []
for index, m in enumerate([5,5,5]):
K = 32/np.sqrt(m)
ax.append(fig.add_subplot(3, 3, 3*index+1))
ax.append(fig.add_subplot(3, 3, 3*index+2))
ax.append(fig.add_subplot(3, 3, 3*index+3))
for n in [16, 32, 64, 128, 256]:
seed = 100
np.random.seed(seed=seed)
random.seed(seed)
print(n,m)
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_true = Elo_true - (np.mean(Elo_true) - 1500)
Elo_pred = np.ones(n) * 1500
role_true = np.array([0.29, 0.26, 0.21, 0.14, 0.10])
role_pred = np.array([0.20, 0.20, 0.20, 0.20, 0.20])
role_likes_true = np.random.randn(5,n) * 150
role_likes_true -= np.mean(role_likes_true, axis=0)
role_likes_pred = np.zeros((5,n))
l = list(range(n))
loss = []
loss2 = []
loss3 = []
for t in range(40000):
sample = random.sample(l, 2*m)
A_team, B_team = sample[:m], sample[m:]
A_score_true, A_score_pred = np.sum(Elo_true[A_team]*role_true), np.sum(Elo_pred[A_team]*role_pred)
B_score_true, B_score_pred = np.sum(Elo_true[B_team]*role_true), np.sum(Elo_pred[B_team]*role_pred)
for i in range(5):
A_score_true += role_likes_true[i,A_team[i]] * role_true[i]
A_score_pred += role_likes_pred[i,A_team[i]] * role_pred[i]
B_score_true += role_likes_true[i,B_team[i]] * role_true[i]
B_score_pred += role_likes_pred[i,B_team[i]] * role_pred[i]
R_AB_true = A_score_true - B_score_true
R_AB_pred = A_score_pred - B_score_pred
W_AB_true = 1/(1+np.exp(-a*R_AB_true/400))
W_AB_pred = 1/(1+np.exp(-a*R_AB_pred/400))
s = 1 if W_AB_true > np.random.rand() else 0
Elo_pred[A_team] += K * (s - W_AB_pred)
Elo_pred[B_team] -= K * (s - W_AB_pred)
if index in [1,2]:
role_pred += (Elo_pred[A_team]-Elo_pred[B_team])/1500*(s-W_AB_pred)*0.002
role_pred -= (np.sum(role_pred) - 1.0)/5
if index in [2]:
for i in range(5):
role_likes_pred[i,A_team[i]] += (s - W_AB_pred) * 4
role_likes_pred[:,A_team[i]] -= (s - W_AB_pred) * 4/5
role_likes_pred[i,B_team[i]] -= (s - W_AB_pred) * 4
role_likes_pred[:,B_team[i]] += (s - W_AB_pred) * 4/5
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
loss2.append(np.mean(np.abs(role_true-role_pred))*1000)
loss3.append(np.mean(np.abs(role_likes_true-role_likes_pred)))
print(Elo_true[:8])
print(Elo_pred[:8])
print(role_true, role_pred)
print(np.mean(role_likes_pred), np.mean(role_likes_true))
ax[3*index].plot(range(len(loss)), loss, label='n=%d,m=%d'% (n,m))
ax[3*index].set_title('Elo loss')
ax[3*index].legend()
ax[3*index+1].plot(range(len(loss2)), loss2, label='n=%d,m=%d'% (n,m))
ax[3*index+1].set_title('role loss')
ax[3*index+1].legend()
ax[3*index+2].plot(range(len(loss3)), loss3, label='n=%d,m=%d'% (n,m))
ax[3*index+2].set_title('role likes loss')
ax[3*index+2].legend()
plt.show()
別プレイヤー換算
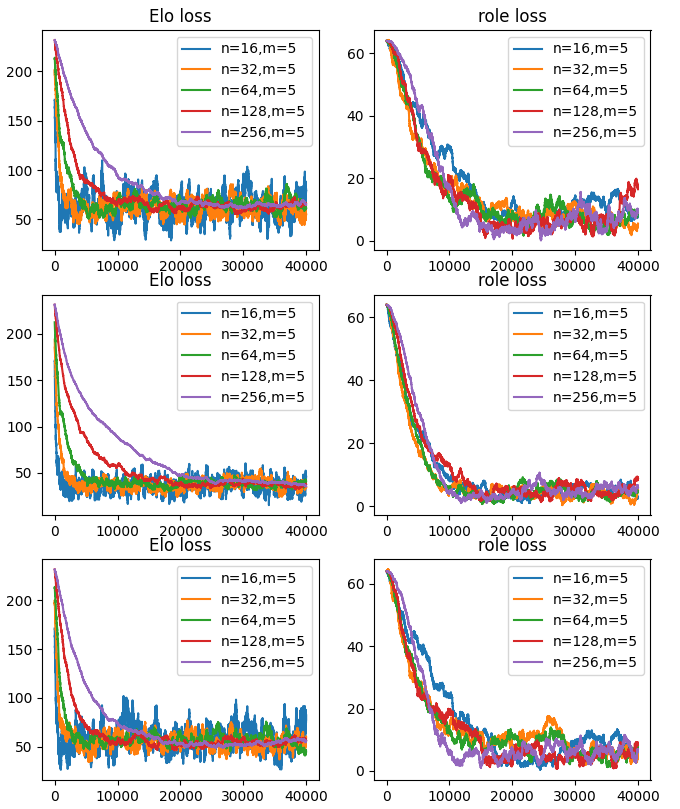
例えば総プレイヤー数が16人で役職の数が5つの時、80人の別プレイヤーのレート移動を想定する。ただし、役職が異なる同一人物でチームを組めないので、80人のランダムマッチとは等価ではない。
更新式は若干簡単になるがEloの収束速度は1/5に悪化するうえ、他の収束を見ても利点がない。Eloのばらつきが280で、役職の得意不得意のばらつきを150としているためそれぞれについて更新量を設定できる前回の更新方法の方が有利なのかもしれない。
import numpy as np
import matplotlib.pyplot as plt
import random
a = np.log(10)
fig = plt.figure()
ax = []
for index, m in enumerate([5]):
K = 32/np.sqrt(m)
ax.append(fig.add_subplot(3, 3, 3*index+1))
ax.append(fig.add_subplot(3, 3, 3*index+2))
ax.append(fig.add_subplot(3, 3, 3*index+3))
for n in [16, 32, 64, 128, 256]:
seed = 100
np.random.seed(seed=seed)
random.seed(seed)
print(n,m)
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_true = Elo_true - (np.mean(Elo_true) - 1500)
Elo_pred = np.ones((5,n)) * 1500
role_true = np.array([0.29, 0.26, 0.21, 0.14, 0.10])
role_pred = np.array([0.20, 0.20, 0.20, 0.20, 0.20])
role_likes_true = np.random.randn(5,n) * 150
role_likes_true -= np.mean(role_likes_true, axis=0)
l = list(range(n))
loss = []
loss2 = []
loss3 = []
for t in range(40000):
sample = random.sample(l, 2*m)
A_team, B_team = sample[:m], sample[m:]
A_score_true, B_score_true = np.sum(Elo_true[A_team]*role_true), np.sum(Elo_true[B_team]*role_true)
A_score_pred, B_score_pred = 0.0, 0.0
for i in range(5):
A_score_true += role_likes_true[i,A_team[i]] * role_true[i]
B_score_true += role_likes_true[i,B_team[i]] * role_true[i]
A_score_pred += Elo_pred[i,A_team[i]] * role_pred[i]
B_score_pred += Elo_pred[i,B_team[i]] * role_pred[i]
R_AB_true = A_score_true - B_score_true
R_AB_pred = A_score_pred - B_score_pred
W_AB_true = 1/(1+np.exp(-a*R_AB_true/400))
W_AB_pred = 1/(1+np.exp(-a*R_AB_pred/400))
s = 1 if W_AB_true > np.random.rand() else 0
for i in range(5):
Elo_pred[i,A_team[i]] += K * (s - W_AB_pred)
Elo_pred[i,B_team[i]] -= K * (s - W_AB_pred)
role_pred[i] += (Elo_pred[i,A_team[i]]-Elo_pred[i,B_team[i]])/1500*(s-W_AB_pred)*0.002
role_pred -= (np.sum(role_pred) - 1.0)/5
loss.append(np.mean(np.abs(Elo_true-np.mean(Elo_pred, axis=0))))
loss2.append(np.mean(np.abs(role_true-role_pred))*1000)
loss3.append(np.mean(np.abs(role_likes_true-(Elo_pred-np.mean(Elo_pred, axis=0)))))
print(Elo_true[:8])
print(Elo_pred[0,:8])
print(role_true, role_pred)
ax[3*index].plot(range(len(loss)), loss, label='n=%d,m=%d'% (n,m))
ax[3*index].set_title('Elo loss')
ax[3*index].legend()
ax[3*index+1].plot(range(len(loss2)), loss2, label='n=%d,m=%d'% (n,m))
ax[3*index+1].set_title('role loss')
ax[3*index+1].legend()
ax[3*index+2].plot(range(len(loss3)), loss3, label='n=%d,m=%d'% (n,m))
ax[3*index+2].set_title('role likes loss')
ax[3*index+2].legend()
plt.show()
対面レート差の二乗項
LoLなどのMOBAを考えた場合、勝負に影響を与えるパフォーマンスは如何に自分の操作キャラを成長させるかという事が重要である。一般に同じ上手さのプレイヤーでも成長具合は対面の敵の強さに依存する。自分のプレイングが同じでも対面の敵が弱いと自分は良く育つし、敵が強いと自分はあまり育たない。そしてその成長速度は現時点の成長中のパフォーマンス差に比例する。従っていったん差が生じるとその差は雪だるま式にどんどん大きくなる。
現在はパフォーマンス差を以下の様に定義してる。
$perf_i=role_i*(R_{A,i}-R_{B,i})$
$\frac{\partial perf}{\partial R_A}=1$
$\frac{\partial perf}{\partial R_B}=-1$
$\frac{\partial perf}{\partial role}=(R_{A,i}-R_{B,i})$
対面係数や優勢係数(DC)と呼ばれるものを考慮する体系においてはレート比率を掛けて以下の様にプレイヤーレートの二乗項に比例する。
$perf_i=role_i*(R_{A,i}\frac{R_{A,i}}{R_{B,i}}-R_{B,i}\frac{R_{B,i}}{R_{A,i}})$
これを以下の様にしてみたい。
$perf_i=role_i*(R_{A,i}-R_{B,i})*abs(R_{A,i}-R_{B,i})$
$perf_i=role_i*(R_{A,i}-R_{B,i})^2*sign(R_{A,i}-R_{B,i})$
この時、更新項は
$\frac{\partial perf}{\partial R_A}\propto2(R_{A,i}-R_{B,i})$
$\frac{\partial perf}{\partial R_B}\propto2(R_{A,i}-R_{B,i})$
$\frac{\partial perf}{\partial role}\propto(R_{A,i}-R_{B,i})^2$
となるが全員の初期レートが1500であればレート差はゼロであり、常に勾配がゼロになるためこの更新項を考えても上手く行かない。ここで正確ではないが以下の様な二回微分が与えられたとして
$\frac{\partial^2 perf}{\partial R_A^2}=2$
$\frac{\partial^2 perf}{\partial R_B^2}=-2$
$\frac{\partial^2 perf}{\partial role\partial R_A}=2(R_{A,i}-R_{B,i})$
以下の様な更新式を考える。
$R_{A new}=R_{A old}+\eta\frac{\partial perf}{\partial R_A} +\frac{\eta^2}{2}\frac{\partial^2 perf}{\partial R_A^2}$
更に一階微分の項を無視すれば二回微分の更新式は従来のパフォーマンス差がレート差に比例する更新式と等しくなる。こう考えると更新項を修正せずともパフォーマンス差が対面レート差の二乗に比例する場合も求められる。
パフォーマンス関数を以下の三つのパターンで更新関数を従来から変えずに収束を確認した。
$perf_i=role_i*(R_{A,i}-R_{B,i})$
$perf_i=role_i*(R_{A,i}\frac{R_{A,i}}{R_{B,i}}-R_{B,i}\frac{R_{B,i}}{R_{A,i}})$
$perf_i=role_i*(R_{A,i}-R_{B,i})*abs(R_{A,i}-R_{B,i})$
ただし、パフォーマンス関数の定義によってEloの収束速度や最終到達lossに若干の差が見られるし、厳密に議論するならば更新項は同じにはならない。
import numpy as np
import matplotlib.pyplot as plt
import random
a = np.log(10)
fig = plt.figure()
ax = []
for index, m in enumerate([5,5,5]):
K = 32/np.sqrt(m)
ax.append(fig.add_subplot(3, 2, 2*index+1))
ax.append(fig.add_subplot(3, 2, 2*index+2))
for n in [16, 32, 64, 128, 256]:
seed = 100
np.random.seed(seed=seed)
random.seed(seed)
print(n,m)
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_true = Elo_true - (np.mean(Elo_true) - 1500)
Elo_pred = np.ones(n) * 1500
role_true = np.array([0.29, 0.26, 0.21, 0.14, 0.10])
role_pred = np.array([0.20, 0.20, 0.20, 0.20, 0.20])
l = list(range(n))
loss = []
loss2 = []
for t in range(40000):
sample = random.sample(l, 2*m)
A_team, B_team = sample[:m], sample[m:]
if index==0:
R_AB_true = np.sum(role_true * (Elo_true[A_team] - Elo_true[B_team]))
R_AB_pred = np.sum(role_pred * (Elo_pred[A_team] - Elo_pred[B_team]))
if index==1:
R_AB_true = np.sum(role_true * (Elo_true[A_team]**2/Elo_true[B_team] - Elo_true[B_team]**2/Elo_true[A_team]))
R_AB_pred = np.sum(role_pred * (Elo_pred[A_team]**2/Elo_pred[B_team] - Elo_pred[B_team]**2/Elo_pred[A_team]))
if index==2:
R_AB_true = np.sum(role_true * (Elo_true[A_team] - Elo_true[B_team])*np.abs(Elo_true[A_team] - Elo_true[B_team])/400)
R_AB_pred = np.sum(role_pred * (Elo_pred[A_team] - Elo_pred[B_team])*np.abs(Elo_pred[A_team] - Elo_pred[B_team])/400)
W_AB_true = 1/(1+np.exp(-a*R_AB_true/400))
W_AB_pred = 1/(1+np.exp(-a*R_AB_pred/400))
s = 1 if W_AB_true > np.random.rand() else 0
Elo_pred[A_team] += K * (s - W_AB_pred)
Elo_pred[B_team] -= K * (s - W_AB_pred)
role_pred += (Elo_pred[A_team]-Elo_pred[B_team])/1500*(s-W_AB_pred)*0.002
role_pred -= (np.sum(role_pred) - 1.0)/5
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
loss2.append(np.mean(np.abs(role_true-role_pred))*1000)
print(Elo_true[:8])
print(Elo_pred[:8])
print(role_true, role_pred)
ax[2*index].plot(range(len(loss)), loss, label='n=%d,m=%d'% (n,m))
ax[2*index].set_title('Elo loss')
ax[2*index].legend()
ax[2*index+1].plot(range(len(loss2)), loss2, label='n=%d,m=%d'% (n,m))
ax[2*index+1].set_title('role loss')
ax[2*index+1].legend()
plt.show()
前述の論文では以下の様な更新式があり、勝った場合はチーム平均のパフォーマンスより大きいパフォーマンスを生じさせたプレイヤーのレート更新量をより大きくしているように見える。一方、負けた場合はチーム平均のパフォーマンスより少ないパフォーマンスを生じさせたプレイヤーのレート更新量をより大きくしているように見える。
この更新量でplotしてみたが、損失的には特にメリットを感じなかった。
高いパフォーマンスを発揮した強いプレイヤーは勝つと大きくレートが上がりやすく、負けてもチーム平均以上のパフォーマンスさえ出してればあまりレートは下がりにくい。強いプレイヤーはレート以上に一人でも試合を破壊できるので過剰にレートを高めに見積もった方がプレイヤーの平均レートを合わせるマッチングにおいて公平だという事なのだろうか。
また、この論文では他の論文を引用して、MOBAの戦いは一般的にmidとbottomレーンが支配的だと言っている。
u = (role_pred * Elo_pred[A_team]**2/Elo_pred[B_team])/np.mean(role_pred * Elo_pred[A_team]**2/Elo_pred[B_team])
v = (role_pred * Elo_pred[B_team]**2/Elo_pred[A_team])/np.mean(role_pred * Elo_pred[B_team]**2/Elo_pred[A_team])
for i in range(5):
Elo_pred[A_team[i]] += K * (s - W_AB_pred) * (u[i])
Elo_pred[B_team[i]] -= K * (s - W_AB_pred) * (1/v[i])
role_pred += (Elo_pred[A_team]-Elo_pred[B_team])/1500*(s-W_AB_pred)*0.002
role_pred -= (np.sum(role_pred) - 1.0)/5
パフォーマンス差は対面レート差の二乗に比例するか?
5vs5のMOBAについて考える。
新たなパフォーマンス差の増加量が現在のパフォーマンス差に比例する時、これは指数関数的である。例えばある単位時間あたりにパフォーマンス差が1.1倍になるとするとこれは$(\frac{11}{10}n)^t$となる。
一方、パフォーマンス差はレベル差とアイテム差(ゴールド差)に依存し、これらの差がレート差に比例し、かつ時間に比例して広がるなら二次関数的かもしれない。例えば$(10.0+t+0.2t)^2-(10.0+t-0.2t)^2$となる。しかしこれはパフォーマンス差が広がる事によってさらに増加量が加速する項は考えてない。
前述した論文にあるパフォーマンス差は$perf_i=role_i*(R_{A,i}\frac{R_{A,i}}{R_{B,i}}-R_{B,i}\frac{R_{B,i}}{R_{A,i}})$に従うとすればレート1500とレート100~2900のパフォーマンス差を確認すると、極端にレートの低い相手でパフォーマンス差が増えるが逆に高い相手では言うほど二次関数的でもない。
また、LoLには敵を倒した場合の獲得賞金が一定ではなく、何度も勝っていると減り、何度も負けていると増える。これは差を広げる向きとは逆向きに働くため時間あたりに広がるパフォーマンス差には上限がある。
また、ジャングルや隣接レーンから助けに来ることもあるため対面レート差だけでなく、隣接レーンのレート差もパフォーマンス差に影響を与える。
また、パフォーマンス差がほぼなくても死ぬまで殴り合ったら体力を僅かに残して必ずどちらかが勝つ。この時、パフォーマンス差の広がりは加速しよう。
また、試合10分時点の各レーンのKDA(kills/deaths/assists)からパフォーマンス差を推定する事も出来よう。
これらを考えるとパフォーマンス差は対面レート差の二乗と役職重みの積に比例するというのは浅い考察でしかなく、実際はさらに複雑である。
まとめ
5vs5のランダムマッチングにおいて役職重みの推定や役職の得手不得手の推定について検討してみた。Trueskillを使わないEloベースの更新方法でも$role_{new,i}=role_{old,i}+(R_{A,i}-R_{B,i})*(s-W_{AB})$に比例する更新項を与えることで役職重みを推定できる。