Kaggleで無作為にサブミットして正解を調べる回数の見積もり その２

前回の記事では非適応戦略では28bitあたり14回のチェックで同定する手法を示した。
これ以上は何故か一意に解くことが出来なくなったため、以降詳しくは書いていない。
とはいえ問題が発生する確率は当初の見積もりよりも非常に低い確率であったので**「高確率で同定可能な手法」**という但し書きが可能ならもっと28bitあたり14回よりも高効率で同定が可能である。
一意に解ける係数は求められていないが、高確率では解けるのでその係数を参考にメモしておく。

#解11 15/32*N回
4bitのチェック関数である$bit4(a,b,c,d)$を仮定して立ててみた。今までの傾向から1個のbitは値が1回だけ、残りの3bitは15回中8回が値が1にならなければならない。この傾向は以下の手順から推測される。

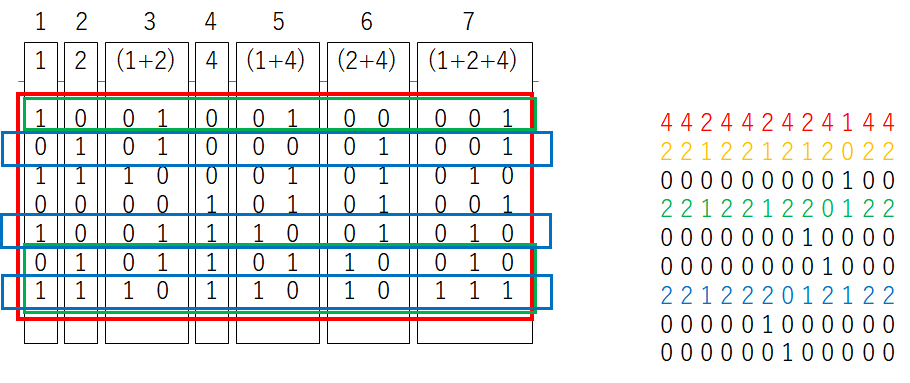
例えば12bitを7回のチェックで同定する手法では7回のチェックの合計値(赤枠の総和)は4,4,2,4,4,2,4,2,4,1,4,4となっている。
これを2で割った商が2,2,1,2,2,1,2,1,2,0,2,2、2で割った余りが0,0,0,0,0,0,0,0,0,1,0,0である。ここで10bit目が同定される。
次に緑枠の合計値は2,2,1,2,2,1,2,2,0,1,2,2なので前述の商と余りの和との差は0,0,0,0,0,0,0,-1,2,0,0,0となる。この値の2で割った時の商と余りから8bit目と9bit目が同定できる。
同様に青枠の合計値との計算で6bit目と7bit目が同定できる。
また同様に4bit目の合計が0になるように合計枠を選べば3bit目と4bit目が同定できる。

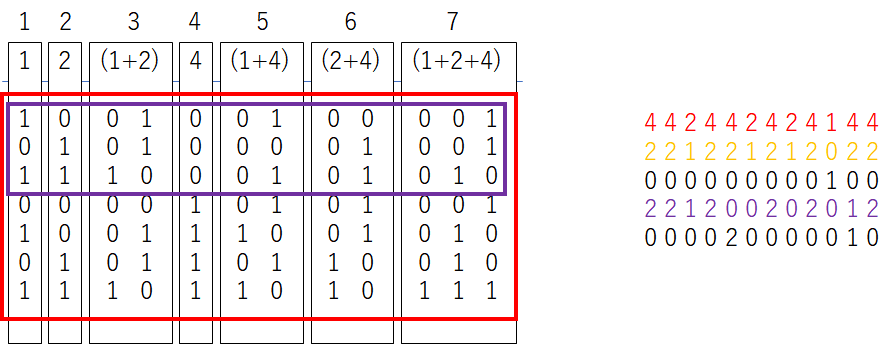
次に紫枠(5bit目の合計が0になるように合計枠)の合計値を考えれば今、6bit目と8bit目は同定されているから差分は0,0,0,0,2,0,0,0,0,0,1,0である。これの2で割った時の商と余りから5bit目と11bit目が同定される。
また同様に1bit目の合計が0になるように合計枠を選べば1bit目が同定できる。
また同様に2bit目の合計が0になるように合計枠を選べば2bit目が同定できる。

このように見ていけば$bit2(a,b)$の3回チェック時点の合計値は$(1,2)$
$bit3(a,b,c)$の7回チェック時点の合計値は$(1,4,4)$だから
$bit4(a,b,c,d)$の15回チェック時点の合計値は$(1,8,8,8)$となることが推測される。

import numpy as np
from sympy import *

def test(y_pred, y_true):
    return len(y_pred) - np.sum(np.abs(y_pred - y_true))

def bit2(a,b):
    value = int(a + b)
    r = np.array(list(format(value, '02b'))).astype('int64')
    return r

def bit3(a,b,c):
    value = int(a + b + c)
    if (a,b,c)==(1,1,1):
        value += 4
    r = np.array(list(format(value, '03b'))).astype('int64')
    return r

def bit4(a,b,c,d):
    r1,r2,r3 = [3, 5, 6, 8, 9,10,12,15], [1, 2, 3, 7,12,13,14,15], [1, 2, 4, 7,11,12,14,15]
    value = 0
    r0 = int(a + 2 * b + 4 * c + 8 * d)
    if r0==15:
        value += 8
    if r0 in r1:
        value += 4
    if r0 in r2:
        value += 2
    if r0 in r3:
        value += 1
    r = np.array(list(format(value, '04b'))).astype('int64')

    return r

def Solve11(length):
    global iter
    m = 15
    Am = 32
    M = np.zeros((Am,m))
    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8]]
    index_list = []
    k = 0
    for i in range(m):
        index_list.append(k)
        k += len(M_list[i])

    k = 0
    for i in range(m):
        index = index_list[i]
        if len(M_list[i])==1:
            for j in range(m):
                M[index,j] = np.array(list(format(j+1, '06b'))).astype('int64')[-1-k]
            k += 1
        if len(M_list[i])==2:
            index2 = index_list[M_list[i][0]-1]
            index3 = index_list[M_list[i][1]-1]
            for j in range(m):
                M[index:index+2,j] = bit2(M[index2,j], M[index3,j])
        if len(M_list[i])==3:
            index2 = index_list[M_list[i][0]-1]
            index3 = index_list[M_list[i][1]-1]
            index4 = index_list[M_list[i][2]-1]
            for j in range(m):
                M[index:index+3,j] = bit3(M[index2,j], M[index3,j], M[index4,j])
        if len(M_list[i])==4:
            index2 = index_list[M_list[i][0]-1]
            index3 = index_list[M_list[i][1]-1]
            index4 = index_list[M_list[i][2]-1]
            index5 = index_list[M_list[i][3]-1]
            for j in range(m):
                M[index:index+4,j] = bit4(M[index2,j], M[index3,j], M[index4,j], M[index5,j])
        if len(M_list[i])==5:
            index2 = index_list[M_list[i][0]-1]
            index3 = index_list[M_list[i][1]-1]
            index4 = index_list[M_list[i][2]-1]
            index5 = index_list[M_list[i][3]-1]
            index6 = index_list[M_list[i][4]-1]
            for j in range(m):
                M[index:index+5,j] = bit5(M[index2,j], M[index3,j], M[index4,j], M[index5,j], M[index6,j])

    y_check = np.array([1] * int(Am))
    result = np.array([0]*m)
    x = [Symbol('x%d' % (i)) for i in range(Am)]
    
    for index in range(0,length//Am*Am,Am):
        y_true2 = y_true[index:index+Am]
        for j in range(m):
            result[j] = test(y_check[:np.count_nonzero(M[:,j])], y_true2[M[:,j]==1])
            iter += 1

        eq = []
        for i in range(Am):
            eq.append(x[i] * x[i] - x[i])
        for j in range(m):
            eq0 = 0
            for i in range(Am):
                eq0 += M[i,j] * x[i]
            eq.append(eq0 - result[j])
        y_pred[index:index+Am] = np.array(solve(eq, x)[0])
        print(index, test(y_pred[index:index+Am], y_true[index:index+Am]))

n = 1024*16
iter = 0
y_pred = np.array([0] * n)
y_true = np.random.randint(0, 2, (n))
Solve11(n)
print(iter, test(y_pred, y_true))

------------------------------
...
6688 32
6720 32
6752 32
6784 18 <= failure!!!
6816 32
6848 32

適当に$bit4(a,b,c,d)$関数を立てて計算させてみるが、これを実行した場合に**低確率で失敗する。**とはいえ16384bitで1回現れる程度なので確率的には低い。勿論、出ない時もある。
これは$bit4(a,b,c,d)$関数が一意に求めるには正しくないのかもしれない。(とはいえ自分の方でも適当な乱数で少しは探したのでこの値は適当に決めた係数の中ではましな方である)

#解12 30/75*N回
その次に$bit5(a,b,c,d,e)$関数が出てくるのは$m=31,Am=80$である。ということは$bit4(a,b,c,d)$関数で書けるのはその一つ前までだから$m=30,Am=75$で求める。これは75bitあたり30回のチェックで同定できるから効率的には0.4である。

def Solve12(length):
    global iter
    m = 30
    Am = 75
    M = np.zeros((Am,m))
    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16]]
------------------------------
...
1500 75
1575 75
1650 62 <= failure!!!
1725 75
...
10500 75
10575 62 <= failure!!!
10650 75
10725 75
10800 55 <= failure!!!
10875 75
...
13875 75
13950 60 <= failure!!!
14025 75
...
15150 75
15225 60 <= failure!!!
15300 75

失敗の件数は16384bit(75bitは218回)で5回程度で解11よりは高い。
とはいえ98%は成功するのでテストデータが1000個程度ならほとんど失敗しないだろう。

#解13 31/80*N回
$bit5(a,b,c,d,e)$の31回チェック時点の合計値は$(1,16,16,16,16)$となることが推測される。
この数字を合計16となるように決めて実行した所、以下の様な$bit5$関数を定義した。

def bit5(a,b,c,d,e):
    r01 = [2, 3, 5,10,13,14,15,16,19,20,21,22,27,29,30,31]
    r02 = [1, 2, 4, 6, 9,10,11,13,15,17,19,21,26,29,30,31]
    r03 = [2, 3, 4, 7, 8,11,12,13,14,16,18,22,24,28,30,31]
    r04 = [2, 5, 6, 7, 9,10,13,14,16,19,23,24,25,26,28,31]
    value = 0
    r0 = int(a+2*b+4*c+8*d+16*e)

    if r0==31:
        value += 16
    if r0 in r01:
        value += 8
    if r0 in r02:
        value += 4
    if r0 in r03:
        value += 2
    if r0 in r04:
        value += 1
    r = np.array(list(format(value, '05b'))).astype('int64')

    return r

def Solve13(length):
    global iter
    m = 31
    Am = 80
    M = np.zeros((Am,m))
    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16], [1,2,4,8,16]]

失敗の件数は1024*16bit(80bitは204回)で3回程度で解13とさほど変わらない。というか解13よりも少ない。

#解14 62/186N回
$bit5(a,b,c,d,e)$関数で作れるのは$bit6(a,b,c,d,e,f)$関数が出てくる$m=63,Am=192$の一歩前、つまり$m=62,Am=186$までである。効率は0.333でテストデータの$1/3$回のチェックで同定が出来る。これは理論上限が$αN/log_{2}N$で$2≦α≦log_{2}9(3.17)$より$N=1024$の場合、$200～320$と見積もられるからその値に近い。

しかし、問題は計算に非常に時間が掛かることである。

def Solve14(length):
    global iter
    m = 62
    Am = 186
    M = np.zeros((Am,m))
    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16], [1,2,4,8,16],
              [32], [1,32], [2,32], [1,2,32], [4,32], [1,4,32], [2,4,32], [1,2,4,32], [8,32], [1,8,32], [2,8,32], [1,2,8,32], [4,8,32], [1,4,8,32], [2,4,8,32], [1,2,4,8,32],
              [16,32],[1,16,32],[2,16,32],[1,2,16,32],[4,16,32],[1,4,16,32],[2,4,16,32],[1,2,4,16,32],[8,16,32],[1,8,16,32],[2,8,16,32],[1,2,8,16,32],[4,8,16,32],[1,4,8,16,32],[2,4,8,16,32]] 

#時間比較
実行時間の比較を行ってみる。16384bitの長さのチェックを$m=14,15,30,31,47,62$の時間と失敗数をメモする。

    m = 14
    Am = 28
    M = np.zeros((Am,m))
    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8]]

#    m = 15
#    Am = 32
#    M = np.zeros((Am,m))
#    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8]]

#    m = 30
#    Am = 75
#    M = np.zeros((Am,m))
#    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
#              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16]]

#    m = 31
#    Am = 80
#    M = np.zeros((Am,m))
#    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
#              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16], [1,2,4,8,16]]

#    m = 47
#    Am = 128
#    M = np.zeros((Am,m))
#    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
#              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16], [1,2,4,8,16],
#              [32], [1,32], [2,32], [1,2,32], [4,32], [1,4,32], [2,4,32], [1,2,4,32], [8,32], [1,8,32], [2,8,32], [1,2,8,32], [4,8,32], [1,4,8,32], [2,4,8,32], [1,2,4,8,32]]

#    m = 62
#    Am = 186
#    M = np.zeros((Am,m))
#    M_list = [[1], [2], [1,2], [4], [1,4], [2,4], [1,2,4], [8], [1,8], [2,8], [1,2,8], [4,8], [1,4,8], [2,4,8], [1,2,4,8],
#              [16], [1,16], [2,16], [1,2,16], [4,16], [1,4,16], [2,4,16], [1,2,4,16], [8,16], [1,8,16], [2,8,16], [1,2,8,16], [4,8,16], [1,4,8,16], [2,4,8,16], [1,2,4,8,16],
#              [32], [1,32], [2,32], [1,2,32], [4,32], [1,4,32], [2,4,32], [1,2,4,32], [8,32], [1,8,32], [2,8,32], [1,2,8,32], [4,8,32], [1,4,8,32], [2,4,8,32], [1,2,4,8,32],
#              [16,32],[1,16,32],[2,16,32],[1,2,16,32],[4,16,32],[1,4,16,32],[2,4,16,32],[1,2,4,16,32],[8,16,32],[1,8,16,32],[2,8,16,32],[1,2,8,16,32],[4,8,16,32],[1,4,8,16,32],[2,4,8,16,32]]

m	14	15	30	31	47	62
Am	28	32	75	80	128	186
効率(m/Am)	0.500	0.469	0.400	0.388	0.367	0.333
実行数(16384bit/Am)	585	512	218	204	128	88
失敗数	0	1	5	3	5	-
実行時間	730[s]	986[s]	4883[s]	6255[s]	18709[s]	-
実行時間/実行数	1.3[s]	1.9[s]	22.4[s]	30.7[s]	146[s]	1117[s]
$m=62$では時間が掛かりすぎて終わらなかった。何故か途中で止まってしまっている。
演算時間は$m=62$以外では$Am^3$にほぼ比例している。その領域の関係式でいえば$m=62$の実行時間/実行数は$400[s]$程度が妥当である。
$m=15$以降ではやはり低確率で失敗してしまうので$bit4,bit5$関数の係数の決め方が良くないと思われる。
とはいえTaitanic問題はテストデータが418件と数が多くないのでこの二値分類コンペではこの不完全な手法でも確率的には数回の試行中で失敗する確率は低いと思われる。

#まとめ
低確率で失敗してしまうがサブミット回数はテストデータの約$1/3$(186bitあたり62回のチェック)で済む手法を示した。また、参考までに同様に次の$bit6$関数を定義出来た場合、理論的には$m=126,Am=441$まで定義できる。
Taitanic問題のテストデータ418件を探すとちょうど$m=122,Am=418$であるから418bitの結果は122回のサブミット結果のスコアから答えのラベルを同定できる。効率は0.292で3割を下回る。
しかし、現実的には$m=122$でこの連立方程式を解くのには演算時間が$Am^3$に比例すると仮定しても$4500[s]$かかり、また、失敗する確率も考えると今回の手法では現実的ではない。

また、Kaggleのスコアは少数5桁まで出るのでテストデータが1000件未満のサブミット時の正解bitの数を求めるのは容易である。例えば上記なら正解数は$158/418$である。