"Inductive Representation Learning on Large Graphs"の数値実験で前処理として使われていたので、興味をもち読んだ。
情報
- A Simple but Tough-to-Beat Baseline for Sentence Embeddings
- この記事の画像は上記論文からの転載。
簡単にまとめると
- センテンスのembeddingを計算するシンプルな方法を提案している。
- センテンスに現れる単語の生成確率をモデル化して近似した最尤推定量を求めている。
1 Introduction
- この論文では、とてもシンプルなsentence embeddingの方法を提案している。
- その方法は、単語のembeddingの加重平均からそのベクトルのfirst principal componentへのプロジェクションを引く。
- ここで、単語$w$ のウエイトは $a / (a + p(w))$ と定義する
- $a$: パラメータ
- $p(w)$: 推計されたword frequency
- この方法をsmooth inverse frequency(SIF)と呼ぶ。
- SIFは様々なタスクでunweighted averageだけでなく、RNNやLSTMを含む洗練された教師ありの手法よりもパフォーマンスが高い。
- この手法はdomain adaptionにより適している。
- SIFの加重平均はTF-IDFと似ているが、documentではなくsentenceを対象にしているので、同じsentenceに重要な単語が何回も出現するとは考えにくい。
- 先行研究(Arora et al., 2016)の方法を修正して理論的正当性を提供する。
2 Related work
Word embeddings
- word embeddingはneural network modelの内部表現として得られる
- または、共起統計のlow rank近似から得られる。
- これら2つの方法は密に関連していることが知られている。
- この論文は、(Arora et al., 2016)と直接的に関連している。その論文では文書中の単語を生成するrandom walk modelを提案している。
Phrase/Sentence/Paragraph embeddings.
- 先行研究では単語の埋め込みに対して行列演算を行うことでセンテンスの埋め込みを計算してきた。
- 要素ごとの演算で良い結果が出ることが示された。また短いフレーズに対してシンプルな平均でも上手くいことが示された。
- 他のアプローチとしてRNNを使った教師あり・なしの手法がある。
3 A simple method for sentence embedding
- (Arora et al., 2016)の洗剤変数生成モデルを紹介する。
- $t$番目の単語はステップ$t$で生成される。
- プロセスはdiscourse vector $c_t \in R^d$のrandom walkにより決められる。
- $c_t$は"何について話されているか"を表す。
- $c_t$とword vector $v_w$の内積は2つのcorrelationを表す。
- $t$時点での単語$w$の生成確率は次で定義する
$$\text{Prob}(w \text{ emitted at time } t | c_t) \propto \exp(c_t \cdot v_w)$$
- $c_t$ はslow random walkを行う。
- つまり$c_{t+1}$は$c_t$にランダムな変位ベクトルを加えることで生成される。
Our improved Random walk model
- この論文で提案する手法では、前述した手法を改善する。
- sentence $s$の1文字が取り除かれたとしても$c_t$は大きく変化しないと仮定し、$c_t$ではなく、$s$のdiscourse vector $c_s$を使う。
- log linear modelに2つのsmoothing termを追加する。
- 1つ目は$\alpha p(w)$。$p(w)$は全コーパス内のユニグラムの確率であり、$\alpha$はスカラー値のパラメータである。
- この項により、$c_s$との内積が小さい単語も生成される。
- 2つ目は共通のdiscourse vector $c_0$を加える。
- この項により、syntaxに関連する要素を加えることができる。
- 結果、生成確率は次のようになる。
$$\text{Prob}(w \text{ emitted at time } t | c_t) = \alpha p(w) + (1 - \alpha) \frac{\exp(c_s \cdot v_w)}{Z_{\tilde{c}_s}}$$
- $\tilde{c}_s = \beta c_0 + (1 - \beta) c_s$
- $c_0 \perp c_s$
- $Z_{c} = \sum_{w \in V} \exp(c \cdot v_w)$
Computing the sentence embedding
- $v_w$が一様に分散していると仮定する。つまり、$Z_c$は$c$に関係なく一定となる。
- このとき尤度は次のようになる。
- $p(s|c_s) = \prod_{w \in s} p(w | c_s) = \prod_{w \in s} (\alpha p(w) + (1 - \alpha) \frac{\exp(v_w \cdot \tilde{c}_s)}{Z})$
- $f_w(c) = \log (\alpha p(w) + (1 - \alpha) \frac{\exp(v_w \cdot c)}{Z})$とすると
- $\nabla f_w(c) = \frac{1}{\alpha p(w) + (1 - \alpha) \exp(v_w \cdot c) / Z} \frac{1 - \alpha}{Z} \exp(v_w \cdot c) v_w$
- 0の周りで1次までのテイラー展開をすると、
$$f_w(c) \approx f_w(0) + \nabla f_w(0)^T c = \text{constant} + \frac{(1- \alpha) / (\alpha Z)}{p(w) + (1 - \alpha) / (\alpha Z)} v_w \cdot c$$
- よって単位球面上の$\tilde{c}_s$の最尤推定量は次のようになる。
$$\arg\max\sum_{w \in s} f_w(\tilde{c}_s)$$
$$ \propto \sum_{w \in s} \frac{\alpha}{p(w) + \alpha} v_w$$
- $a = \frac{1 - \alpha}{\alpha Z}$
- 下記のアルゴリズムで$c_s$を求めることができる。
- 単語のembeddingは予めGolVeやPSL等で計算しておく。

3.1 Connection to subsampling probabilities in word2vec
- そのうち書く(数式が多く書くのが大変なので)
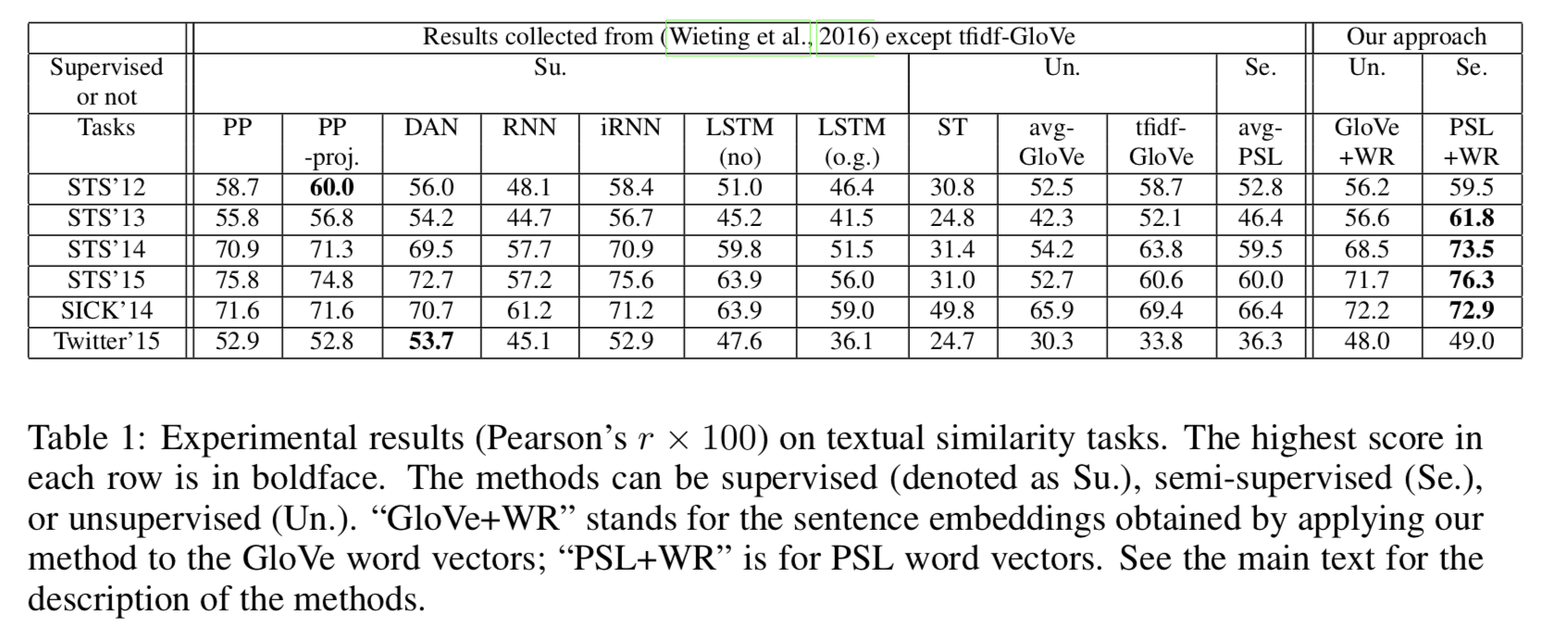
Experiments
- $\alpha=10^{-3}$