この記事は、開発生産性 Advent Calendar 2023の3日目の記事です。
2日目の記事は、luton-mrさんの「垣根を越えればチームが強くなる」とflutter_daisukiさんの「GitHub Copilotの全社導入効果について」でした。
私は、開発生産性の向上のときに立ちはだかる技術的負債の解消について数式から考えてみました。
具体的には、「この技術的負債の解消はやるべきかどうか?」、「負債解消をやるとしたらどのぐらい工数をかけて良いのか?」 といった問いにある程度の合理性を持って回答できないか数式から考えてみました。
はじめに
エンジニアとして経験を積んでくると、「技術的負債の解消は大事!」と思うシーンも増えてくることでしょう。
しかし、顧客に価値を届ける機能開発や機能改善ではなく、技術的負債の解消をしたいといっても、エンジニア以外の人にはなかなか理解されづらいものです。
私もいちエンジニアとしては、技術的負債の解消をすることで、経験則として開発スピードとソフトウェア品質の向上や開発者体験が良くなることがわかります。
しかし、
- 「どれぐらいの技術的負債がある状態において、負債解消をすべきか?」
- 「負債解消するとしたら、どのぐらいの工数をかけてもよいか?」
ということについてはイマイチわかりませんでした。
そのため、大雑把でもいいのでこれらの問いに答えられないかと気になったので技術的負債の解消について数式にしながら考えてみました。
技術的負債とは
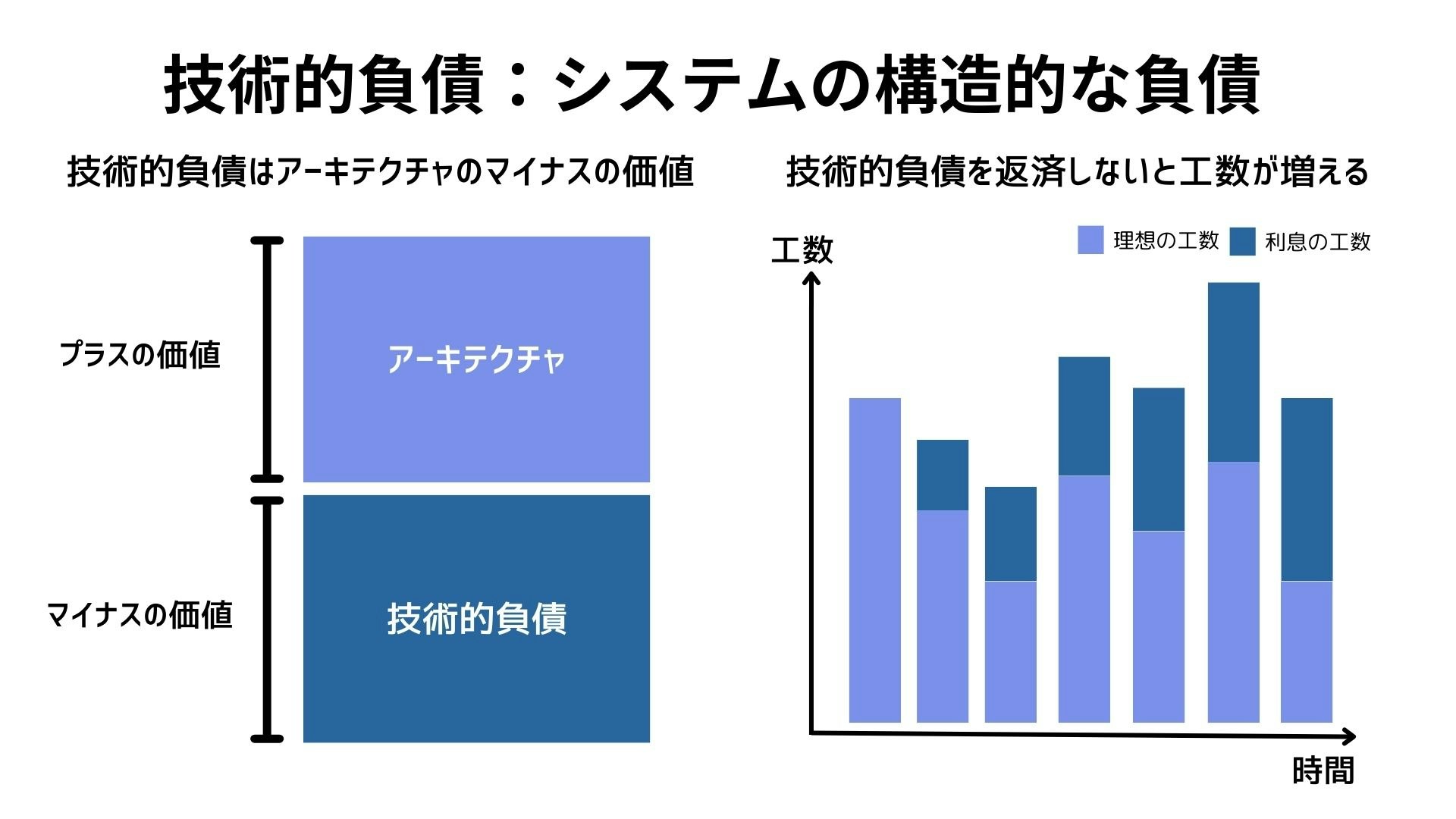
この記事では、技術的負債のことを設計やソースコードなどのシステムの構造的な負債という意味で使っています。
技術的負債が多いとシステムの変更時に余分に時間がかかったり、バグが発生しやすくなります。また、開発していく中でも開発時の調査・考慮事項が増えて開発者体験も悪化してしまいます。
わかりやすいところで言えば以下のようなものがあります。
- コードが重複して修正箇所が多岐に渡る。修正が漏れるとそこがバグになる
- 分岐が複雑で読み解くのに時間がかかる。条件にヌケモレがあるとバグる
- テーブル設計が不適切で、いろいろなデータ状態を考慮しないといけない
- コンポーネント設計がうまくいっておらずコードの見通しが悪くコードを読むのが大変
負債度とは
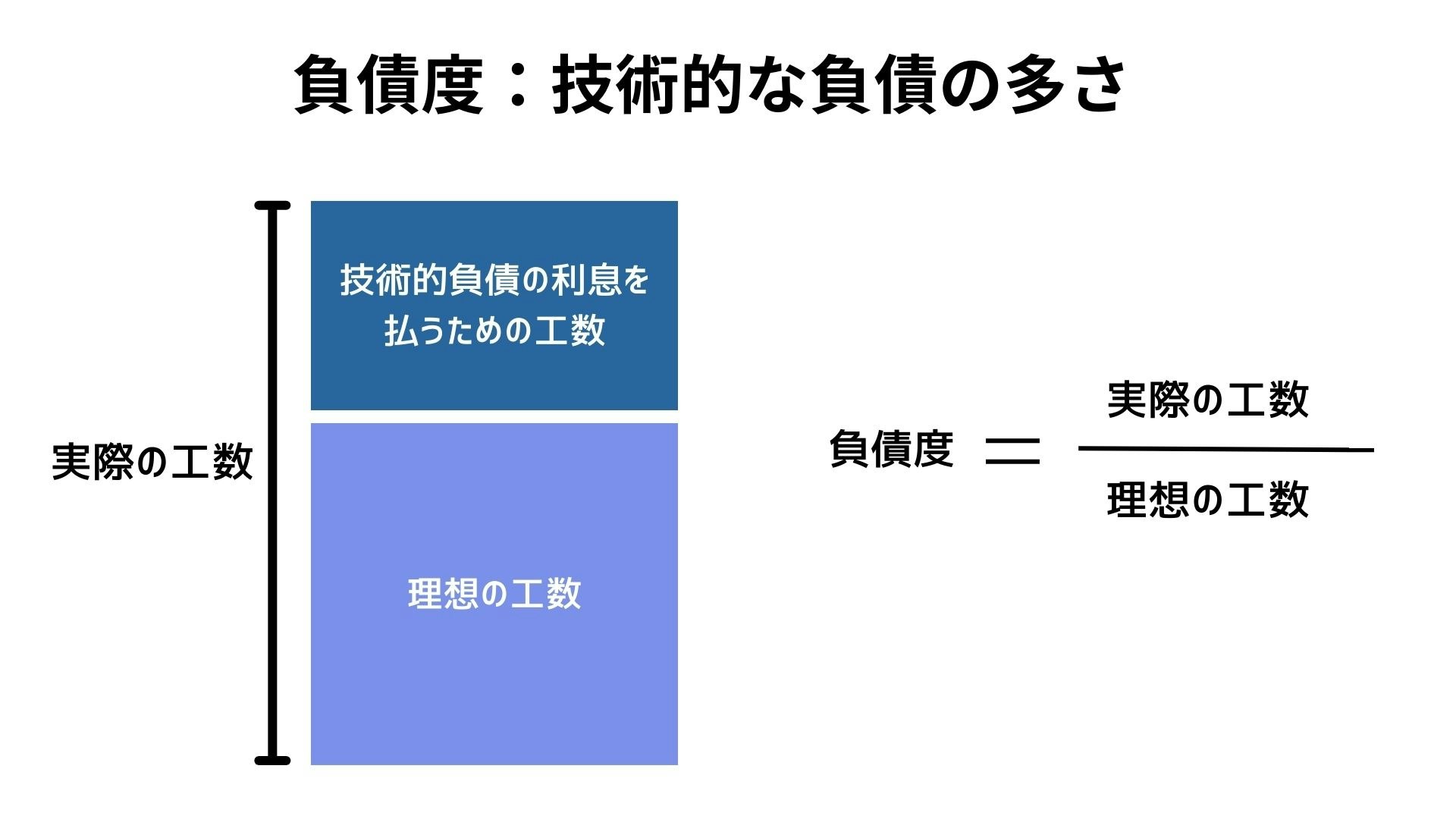
負債度は、説明を簡単にするために私が作った造語で、「技術的負債の多さ」 のことです。
理想の工数に対して実際の工数がどれだけかかってしまったかという度合いとして定義しています。
負債度の計算式
負債度 = 実際の工数 \div 理想の工数
例えば、ある画面の機能改善があったとします。理想では5日かかるところが技術的負債がたくさんあり10日かかったとします。この場合、負債度は 2 となります。
負債度 = 実際の工数 10日 \div 理想の工数 5日 = 2
現実的には難しいですが、負債度の理想的な値は 1 です。負債度が 1 の場合、技術的負債がまったくなく、理想の工数と実際の工数が同じになります。
技術的負債解消の式(簡略版)
前提、アイデアから順を追って技術的負債解消の式(簡略版)を導出していきます。
前提
- 開発をすると技術的負債(負債度)が「指数関数的」に溜まっていく(※簡略版ではこの概念は式にいれていません)
- 技術的負債があることで、変更時に理想の工数に対して余分に工数がかかってしまう
- 技術的負債が多ければ多いほど(負債度が高ければ高いほど)、余分にかかる工数も大きくなる
- 技術的負債の解消の効果は、将来の開発に対して効果がでる
アイデア
- リファクタリングの前後での改修工数を比較
- リファクタリングの実施により、「負債度」が減ることで、「理想の工数」が同じでも「実際の工数」を削減できる
- このリファクタリング前後の「実際の工数」の差分がリファクタリングによる工数削減効果と言えそう
- このリファクタリングによる工数削減効果がリファクタリングの実施工数よりも大きければリファクタリングを実施するのは合理的と言えそう
| 理想の工数 | 負債度 | 実際の工数 | |
|---|---|---|---|
| リファクタリング前 | 10人月 | 2 | 20人月 |
| リファクタリング後 | 10人月 |
1.2 リファクタリングにより 技術的負債が減った |
12人月 負債度が減ったので 実際の工数も減った |
上記のケースの場合、リファクタリングによる工数の削減効果は、8人月(20人月-12人月)となります。
そのため、リファクタリングの対応工数が8人月以下であれば、リファクタリングを実施したほうが合理的と言えそうです。
アイデアから数式の導出
まず、技術的負債解消の効果が負債解消自体の対応自体の工数よりも高いか低いかで負債解消のやるやらの判断に使えそうです。
技術的負債解消の効果 > 技術的負債解消の対応工数
次に、技術的負債解消の効果を分解していきます。
技術的負債の解消の効果はいろいろありますが、話を簡単にするために、技術的負債解消の効果を工数削減効果として定義しています。
\begin{align*}
技術的負債解消の効果 &= 技術的負債解消による工数削減効果 \\
&= 技術的負債解消前の実際の工数 - 技術的負債解消後の実際の工数 \\
&= (技術的負債解消前の負債度 \times \sum将来の変更の理想工数) - (技術的負債解消後の負債度 \times \sum将来の変更の理想工数) \\
&= \sum将来の変更の理想の工数 \times (負債解消前の負債度 - 負債解消後の負債度) \\
\end{align*}
技術的負債解消の式
まとめると、技術的負債解消の式は次のとおりです。
こちらを計算すると、「技術的負債解消をすべきかどうか?」、「負債解消するとしたら、どのぐらいの工数をかけてもよいか?」 といった問いに対して工数観点で「おおまか」に回答できるようになると思います。
「おおまか」と言っているのは、そもそも将来の変更の理想工数や負債度をきっちり把握することはできないためです。
技術的負債解消の対応工数 < \sum将来の変更の理想工数 \times (負債解消前の負債度 - 負債解消後の負債度)
技術的負債解消の式から言えそうなこと
言えそうなこととしては主に4つあります。
①将来変更がたくさんあるなら負債解消をやるのはあり
②負債が多い場合は、負債解消に大胆に工数をかけて負債を一気に返済するとよさそう
③ 負債が少ないなら、ボーイスカウト精神でコツコツ改善するとよさそう
④ 今後の変更がなければ負債解消をしても意味がない
①将来変更がたくさんあるなら負債解消をやるのはあり
将来の変更がたくさんあるということは、将来の変更の理想工数の合計が大きくなります。
技術的負債解消による工数削減効果 = \sum将来の変更の理想工数 \times (負債解消前の負債度 - 負債解消後の負債度)
その上で、「将来の変更が多い」ケースと「将来の変更が少ない」ケースを比較してみます。
将来の変更の理想工数と負債度は掛け算なので、負債度が同じだとした場合、将来の変更が多いほど実際の工数も掛け算で大きくなります。
| ケース | 将来の変更の 理想工数 |
負債度 | 実際の工数 |
|---|---|---|---|
| 将来の変更が多い | 30人月 | 1.5 | 45人月 |
| 将来の変更が少ない | 5人月 | 1.5 | 7.5人月 |
「将来の変更が多い」ケースで仮に負債度を1.5から1まで下げれるのであれば、技術的負債解消の効果は15人月(45人月-30人月)となります。
| ケース | 将来の変更の 理想工数 |
負債度 | 実際の工数 | 技術的負債解消の効果 |
|---|---|---|---|---|
| 将来の変更が多い (負債解消前) |
30人月 | 1.5 | 45人月 | - |
| 将来の変更が多い (負債解消後) |
30人月 | 1.0 | 30人月 | 15人月 |
| 将来の変更が少ない (負債解消前) |
5人月 | 1.5 | 7.5人月 | - |
| 将来の変更が少ない (負債解消後) |
5人月 | 1.0 | 5人月 | 2.5人月 将来の変更が多い場合 に比べ効果が低い |
もちろん、現実的には将来を見通せないので過去実績やプロダクト戦略などから見込みをたてながらも、最後の最後はえいやでやっていく必要があると思っています。
②負債が多い場合は、負債解消に大胆に工数をかけて負債を一気に返済するとよさそう
技術的負債解消の式から負債が多くあり、また、たくさん解消できる場合、負債解消に工数を多くさくことができます。
まず、「負債が多い」ケースと「負債が少ない」ケースを考えていきます。
将来の変更の理想工数と負債度は掛け算なので、負債度が大きいほど実際の工数も掛け算で大きくなります。
| ケース | 将来の変更の 理想工数 |
負債度 | 実際の工数 |
|---|---|---|---|
| 負債が多い | 20人月 | 2.0 | 40人月 |
| 負債が少ない | 20人月 | 1.2 | 24人月 |
次に、「負債が多い」かつ「大きく負債解消できた」と「あまり負債解消できず」のケースを考えてみます。
負債度が減るほど掛け算の対象が減るので実際に掛かる工数も大きく減らせています。
| ケース | 将来の変更の 理想工数 |
負債度 | 実際の工数 | 技術的負債解消の効果 |
|---|---|---|---|---|
| 負債が多い | 20人月 | 2.0 | 40人月 | - |
| 負債が多い (大きく負債解消できた) |
20人月 | 1.0 | 20人月 | 20人月 |
| 負債が少ない | 20人月 | 1.2 | 24人月 | - |
| 負債が少ない (負債解消できた) |
20人月 | 1.0 | 20人月 | 4人月 負債が多い場合に に比べ効果が低い |
上記の負債が多いケースでは、大きく負債解消が見込める場合は、20人月ぐらい(40人月-20人月)かけて負債解消してもよいことになります。
③ 負債が少ないなら、ボーイスカウト精神でコツコツ改善するとよさそう
負債が少ない場合、負債による余計な工数も少ないので、大きく負債解消に工数をかけるのは合理的ではありません。
| ケース | 将来の変更の 理想工数 |
負債度 | 実際の工数 | 技術的負債解消の効果 |
|---|---|---|---|---|
| 負債が多い | 20人月 | 2.0 | 40人月 | - |
| 負債が少ない | 20人月 | 1.2 | 24人月 | - |
| 負債が少ない (負債解消後) |
20人月 | 1.0 | 20人月 | 4人月 |
しかし、負債ははじめは少しずつですが指数関数的に蓄積されていってしまうので、ボーイスカウト精神でコツコツ改善して負債度が爆発しないようにコントロールしていくことが重要だと考えられます。
④ 今後の変更がなければ負債解消をしても意味がない
極端な例ですが、将来の変更がないとどれだけ負債を減らせたとしても負債解消の効果はありません。
\begin{align*}
技術的負債解消の効果 &= 技術的負債解消による工数削減効果 \\
&= 将来の変更の理想工数 0人月 \times (負債解消前の負債度2 - 負債解消後の負債度1) \\
&= 0
\end{align*}
上記の式のように、技術的負債解消の効果は、将来の変更の理想工数と負債度の減少量の掛け算です。将来の変更の理想工数がゼロということは、いくら負債解消しても技術的負債解消の効果はなかったと言えます。
まとめ
今回は、技術的負債の解消について数式から 「この技術的負債の解消はやるべきかどうか?」、「負債解消をやるとしたらどのぐらい工数をかけて良いのか?」 といったことについて考えてみました。
ぜひ、効果的に技術的負債の解消を進めて、開発スピードやソフトウェア品質の向上、開発者体験の向上を実現していただけると嬉しいです。