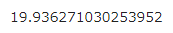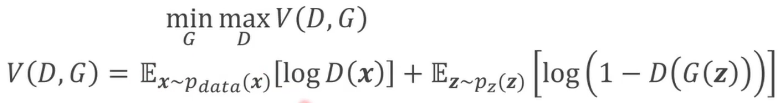More than 3 years have passed since last update.

JDLA E資格検定メモ深層学習2

Posted at 2021-07-04

0. 初めに
1. 再起型ニューラルネットワークの概念
- 1-1. 要点まとめ
- 1-2. 演習
2. LSTM
- 2-1. 要点まとめ
- 2-2. 演習
3. GRU
- 3-1. 要点まとめ
- 3-2. 演習
4. 双方向RNN
- 4-1. 要点まとめ
- 4-2. 演習
5. Seq2Seq
- 5-1. 要点まとめ
- 5-2. 演習
6. Word2Vec
- 6-1. 要点まとめ
- 6-2. 演習
7. Attention Mechanism
- 7-1. 要点まとめ
- 7-2. 演習
8. 強化学習
- 8-1. 要点まとめ
- 8-2. 演習
9. AlphaGo
- 9-1. 要点まとめ
- 9-2. 演習
10. 軽量化・高速化技術
- 10-1. 要点まとめ
- 10-2. 演習
11. 応用モデル
- 11-1. 要点まとめ
- 11-2. 演習
12. Transformer
- 12-1. 要点まとめ
- 12-2. 演習
13. 物体検知・セグメンテテーション
- 13-1. 要点まとめ
- 13-2. 演習
14. DCGAN
- 14-1. 要点まとめ
- 14-2. 演習

0. 初めに

E資格検定の深層学習パート（2/2）についてメモします。
- ここでは深層学習の応用を取り扱う。
各パートについて、要件まとめと演習結果を記載する。

1. 再起型ニューラルネットワークの概念

1-1. 要点まとめ

CNN復習の確認テスト
- サイズ5x5の入力画像を、サイズ3x3のフィルタで畳み込んだ時の出力画像のサイズは？（ストライド:2、パディング:1とする）
  - 公式より、$H = \frac{5+2*1-3}{2}+1 = 3$
  - 正方行列のため、3x3が正解。
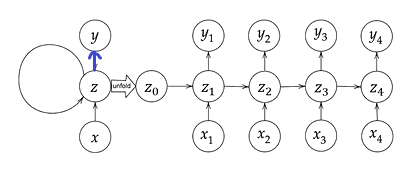
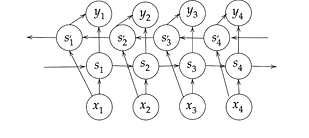
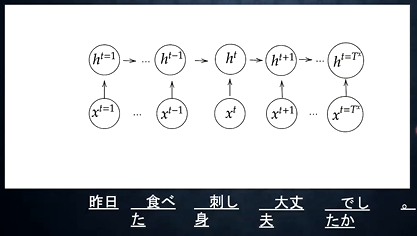
RNNの全体像
- RNNとは
  - 時系列データに対応可能なニューラルネットワーク。
- 時系列データ
  - 時系列データ：時間的なつながりのあるデータ
    - 音声データ、自然言語データ、株価データなど
      - 自然言語データも単語の並びに順序性があるため、時系列データといえる
- RNNにおける工夫
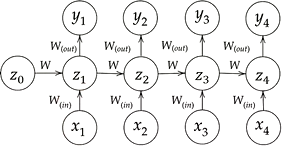
  - 通常のNNは一方通行。RNNでは中間層からの出力を次の中間層の処理の入力に使う
  - RNNでは重みが増える（$W_{(in)}$、$W_{(out)}$、$W$）
  - 順伝播の数式と対応するpythonコード
    - $u_t = W_{(in)} x^t + W z^{t-1} + b$
      - u[:, t+1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
    - $z_t = f \left( W_{(in)} x^t + W z^{t-1} + b \right)$
      - z[:, t+1] = functions.sigmoid(u[:, t+1])
    - $v_t = W_{(out)} z^t + c$
      - np.dot(z[:, t+1].reshape(1, -1), W_out)
    - $y_t = g \left( W_{(out)} z^t + c \right)$
      - y[:, t] = functions.sigmoid(np.dot(z[:, t+1].reshape(1, -1), W_out))

※矢印の向きに誤りがあったとのことで訂正

確認テスト
- RNNのネットワークには大きく分けて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重み。のこり1つの重みについて説明せよ。
- [解答]ひとつ前の時点での中間層から出力された値にかけられる重み。
1回の学習単位
- N単位時間の予測計算を行い、それらをひとまとめてにして1学習単位とする
BPTT（Backpropagation Through Time）
- RNNにおける逆伝播処理のこと
- 数学的記述1と対応するpythonコード
  - 重み $W_{in}, W_{out}, W$
    - $\frac{\partial{E}}{\partial{W_{(in)}}} = \frac{\partial{E}}{\partial{u^t}} \begin{bmatrix} \frac{\partial{u^t}}{\partial{W_{(in)}}} \end{bmatrix}^T = \delta^t \begin{bmatrix} x^t \end{bmatrix}^T $
      - np.dot(X.T, delta[:, t].reshape(1, -1))
    - $\frac{\partial{E}}{\partial{W_{(out)}}} = \frac{\partial{E}}{\partial{v^t}} \begin{bmatrix} \frac{\partial{v^t}}{\partial{W_{(out)}}} \end{bmatrix}^T = \delta^{out,t} \begin{bmatrix} z^t \end{bmatrix}^T $
      - np.dot(z[:, t+1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
    - $\frac{\partial{E}}{\partial{W}} = \frac{\partial{E}}{\partial{u^t}} \begin{bmatrix} \frac{\partial{u^t}}{\partial{W}} \end{bmatrix}^T = \delta^{t} \begin{bmatrix} z^{t-1} \end{bmatrix}^T $
      - np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
  - バイアス $b,c$
    - $\frac{\partial{E}}{\partial{b}} = \frac{\partial{E}}{\partial{u^t}} \frac{\partial{u^t}}{\partial{b}} = \delta^t \hspace{10mm} \frac{\partial{u^t}}{\partial{b}} = 1$
    - $\frac{\partial{E}}{\partial{c}} = \frac{\partial{E}}{\partial{v^t}} \frac{\partial{v^t}}{\partial{c}} = \delta^{out,t} \hspace{5mm} \frac{\partial{v^t}}{\partial{c}} = 1$
  - 補足
    - $\delta$は複雑な微分式を略記。$\delta^t=\frac{\partial{E}}{\partial{u}}, \delta^{out,t}=\frac{\partial{E}}{\partial{v}}$
    - $\begin{bmatrix} \end{bmatrix}^T$は転置ではなく、時間をさかのぼってすべて計算するという意味
- 数学的記述2 $\delta$の計算
  - $\delta^t = \frac{\partial{E}}{\partial{u^t}} = \frac{\partial{E}}{\partial{v^t}} \frac{\partial{v^t}}{\partial{u^t}} = \frac{\partial{E}}{\partial{v^t}} \frac{\partial{ \{ W_{(out)} f \left( u^t \right) + c} \} }{\partial{u^t}} = f' \left( u^t \right) W_{(out)}^T \delta^{out,t}$
    - delta[:, t] = (np.dot(delta[:, t+1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(u[:, t+1])
  - 試しに$\delta^{t-1}$を求める
    - $\delta^{t-1} = \frac{\partial{E}}{\partial{u^{t-1}}} = \frac{\partial{E}}{\partial{u^t}} \frac{\partial{u^t}}{\partial{u^{t-1}}} = \delta^{t} \Bigl\{ \frac{\partial{u^t}}{\partial{z^{t-1}}} \frac{\partial{z^{t-1}}}{\partial{u^{t-1}}} \Bigr\} = \delta^{t} \bigl\{ W f' \left( u^{t-1} \right) \bigr\} $
  - t-z-1戻した値を求める ※t-zとt-z-1の時間的関係性を見て取れる（ここのzは先述のzとは無関係） - $\delta^{t-z-1} = \delta^{t-z} \bigl\{ W f' \left( u^{t-z-1} \right) \bigr\} $
- 数学的記述3 パラメータの更新式
  - 重み
    - $W_{(in)}^{t+1} = W_{(in)}^t - \epsilon \frac{\partial{E}}{\partial{W_{(in)}}} = W_{(in)}^t - \epsilon \sum_{z=0}^{T_t} \delta^{t-z} \begin{bmatrix} x^{t-z} \end{bmatrix}^T$
      - W_in -= learning_rate * W_in_grad
    - $W_{(out)}^{t+1} = W_{(out)}^t - \epsilon \frac{\partial{E}}{\partial{W_{(out)}}} = W_{(out)}^t - \epsilon \delta^{out,t} \begin{bmatrix} z^{t} \end{bmatrix}^T$
      - W_out -= learning_rate * W_out_grad
    - $W^{t+1} = W^t - \epsilon \frac{\partial{E}}{\partial{W}} = W_{(in)}^t - \epsilon \sum_{z=0}^{T_t} \delta^{t-z} \begin{bmatrix} z^{t-z-1} \end{bmatrix}^T$
      - W -= learning_rate * W_grad
  - バイアス
    - $b^{t+1} = b^t - \epsilon \frac{\partial{E}}{\partial{b}} = b^t - \epsilon \sum_{z=0}^{T_t} \delta^{t-z}$
    - $c^{t+1} = c^t - \epsilon \frac{\partial{E}}{\partial{c}} = c^t - \epsilon \delta^{out,t}$
- 誤差関数の数式
  - $\begin{align} E^t &= \mbox{loss} \left( y^t, d^t \right) \\ &= \mbox{loss} \left( g \left( W_{(out)} z^t + c \right), d^t \right) \\ &= \mbox{loss} \left( g \left( W_{(out)} f \left( W_{(in)} x^t + W z^{t-1} + b \right) + c \right), d^t \right) \end{align} $
  - 「$W_{(in)} x^t + W z^{t-1} + b$」に着目して、以下のように順に展開可能。展開すると前の時間t-2が出てくる
    - ⇒ $W_{(in)} x^t + W f \left( u^{t-1} \right) + b$
    - ⇒ $W_{(in)} x^t + W f \left( W_{(in)} x^{t-1} + W z^{t-2} + b \right) + b$
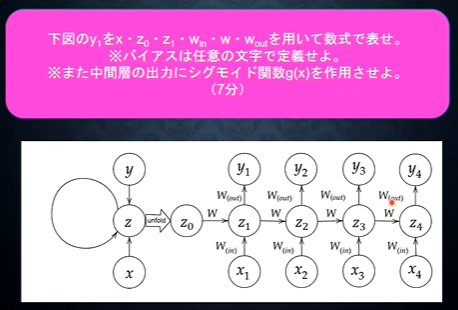
確認テスト
- 解答
  - $s_1 = W_{(in)} x_1 + W s_0 + b$
  - $y_1 = g \left( W_{(out)} s_1 + c \right)$

1-2. 演習

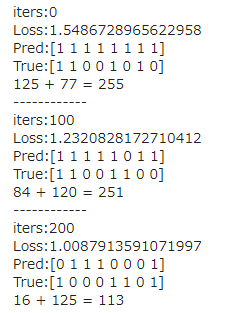
バイナリ加算の学習初期
- 間違いだらけ・・

バイナリ加算の学習終盤
- 正解できている

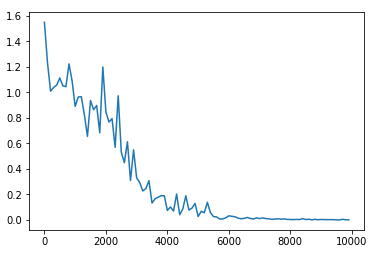
損失の推移
- 順調に学習が進んでいる

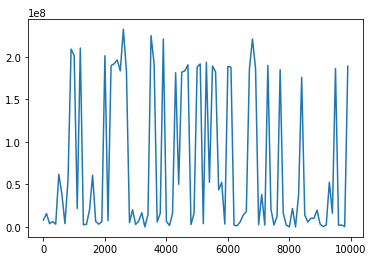
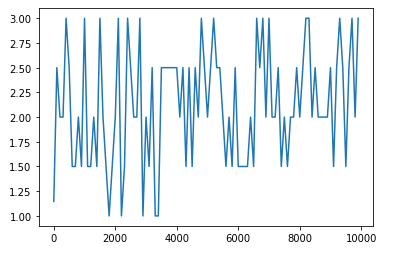
活性化関数をsigmoidからreluへ変更して、勾配爆発の様子を確認

tanh、d_tanhの実装

# tanh関数
def tanh(x):
    return np.tanh(x)
# 導関数（tanh）
def d_tanh(x):
    return 1 - tanh(x)**2

活性化関数をtanhに変更

2. LSTM

2-1. 要点まとめ

RNNの課題
- 時系列をさかのぼるたびに勾配が消失していく ⇒ 長い時系列の学習が困難
- RNNは層が深くなりやすい構造になっている
- 勾配消失が起きづらいネットワーク構造で対処したのがLSTMとなる
確認テスト
- シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値は何か。
- 解答：0.25
  - シグモイド関数の微分 $\left(1 - \mbox{sigmoid}(x) \right) \mbox{sigmoid}(x)$
  - この式が最大となるのは0.5*0.5の時となるため、答えは0.25となる。
勾配爆発
- 逆伝播するたびに勾配がどんどん大きくなる　⇒　学習がうまくいかない
  - 活性化関数に恒等写像を使っている場合に起きることがある
  - 各オプティマイザにおける学習率の推奨値より非常に大きくすると起きる
- 対策：勾配のクリッピング
  - 勾配のノルムが閾値より大きい時に、勾配×（閾値/勾配のノルム）で勾配を閾値に正規化する。
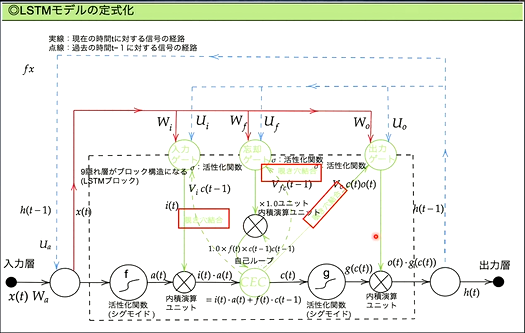
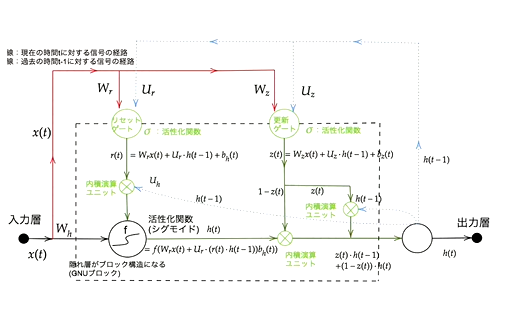
LSTMモデルの定式化
- GRUとともにRNNの一種。

CEC (Constant Error Carousel)
- RNNで言うところの中間層を抜き出したもの
- RNNの問題点として、中間層に過去の記憶をため込むが、ため込みを実現するとき、活性化関数(sigmoidなど）の微分系が多く含まれていることにある。
- CECに過去のだけを記憶を持たせる。「考えること」と「記憶すること」を分離する。
- 勾配消失および勾配爆発の解決策として、過去遡った時の勾配が"1"であれば解決できる
  - $\delta^{t-z-1} = \delta^{t-z} \bigl\{ W f' ( u^{t-z-1} ) \bigr\}$ = 1
  - $\frac{\partial{E}}{\partial{c^{t-1}}} = \frac{\partial{E}}{\partial{c^t}} \frac{\partial{c^t}}{\partial{c^{t-1}}} = \frac{\partial{E}}{\partial{c^t}} \frac{\partial}{\partial{c^{t-1}}} \bigl\{ a^t - c^{t-1} \bigr\} = \frac{\partial{E}}{\partial{c^t}}$
- CECには学習機能がないため、CECの周りに学習機能を配置し、以下を制御する
  - 何を覚えてもらうか（入力ゲート）
  - 覚えたことをどう使うか、（出力ゲート）
入力ゲート
- CECに何を覚えさせるかを学習するのが「入力ゲート」となる
- 「今回の入力値」と「前回の出力値」をもとに、「今回の入力値」をどうCECに覚えさせるのか
出力ゲート
- CECの記憶をどんなふうに使えばいいかを学習するのが「出力ゲート」となる
- 「今回の入力値」と「前回の出力値」をもとに、CECが覚えている内容をどのくらい使うか
- 入力・出力ゲートの役割
  - 入力・出力ゲートを追加することで、それぞれのゲートへの入力値の重みを、重み行列W、Uで変換可能とする。
忘却ゲート
- 過去の情報がいらなくなったタイミングで削除（忘却）できるようにする
覗き穴結合　※大きな改善にはならなかったらしい
- 入力ゲート、出力ゲートの学習の判断材料に、CEC自身の値は影響を与えていない　→　CEC自身の値をゲート制御に使ってみる

2-2. 演習

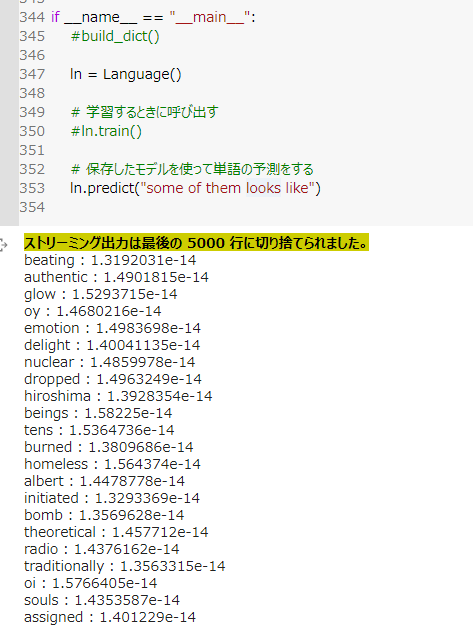
LSTMやGRUを利用して単語予測
- "some of them looks like"の次にくる単語の予測。
- 各単語の出現確率が出ていると思われる

3. GRU

3-1. 要点まとめ

GRUとは？
- LSTMの改良版。LSTMではパラメータが多数存在し、計算負荷が高かった
- GRUでは、パラメータを大幅に削減しつつ、精度は同等またはそれ以上望めるよう構造を改良
- メリットは計算負荷が低いこと

確認テスト
- LSTMとCECが抱える課題について、それぞれ簡潔に述べよ
  - LSTM
    - CECおよびゲート×3の4つの部品を持つことでパラメータ数が多数必要となり、結果として計算量が多くなる
  - CEC
    - 勾配=1で学習能力がないこと。
    - 勾配消失および勾配爆発の対策のため、勾配=1になる。学習能力がないため、学習機能を持つゲートが必要
確認テスト
- LSTMとGRUの違いを簡潔に述べよ
  - GRUには、LSTMにあったCECがないことと、ゲート数が少なくなっている。（LSTM：入力・出力・忘却の3種、GRU：リセット・更新の2種）
  - GRUはLSTMに比べてパラメータ数が少ないため、LSTMよりGRUのほうが計算量が少ない

3-2. 演習

演習なし

4. 双方向RNN

4-1. 要点まとめ

双方向RNNとは？
- RNNの改良版。過去の情報だけでなく、未来の情報も加味することで精度を向上させるモデル
- 実用例
  - 文章の推敲、機械翻訳など

4-2. 演習

演習なし

5. Seq2Seq

5-1. 要点まとめ

Seq2Seqとは？
- 時系列のデータを入力にとり、時系列のデータを出力するモデル
- 2つのNNで構成される。Encoder-Decoderモデルの一種。
- 1つ目のNN（Encoder）
  - 入力された文章の文脈（意味）が隠れ層「C」にベクトル表現として保存される
- 2つ目のNN（Decoder）
  - 保持された文脈をもとに、別の出力に作り替える
- 用途
  - 機械対話、機械翻訳など

Encoder RNN
- 入力されたテキストデータを単語等のトークンに区切って渡す構造
- 最後の文を入力して学習を行ったときのhidden stateをfinal stateとして取っておく。このfinal stateがthought vectorと呼ばれ、入力した分の意味を表すベクトルとなる
- 処理フロー
  - Taking
  - Embedding表現
    - 単語のone-hotベクトルを、数百程度オーダーに大きさに抑え込む
    - 似ている単語は近しいベクトル表現となるように圧縮する

Decoder RNN
- Encoder RNNが出力した隠れ層の状態をもとに、別の文脈を作り出す
- Encoder RNNのfinal state（thought vector）から、各tokenの生成確率を出力する。final stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力
（参考）BERT
- MLM - Masked Language Model
  - 文章の一部をマスクして学習させることで単語の意味ベクトルを獲得する
  - アノテーション（ラベル付け）が不要。多くのデータを集めやすい
確認テスト
- 以下の選択肢から、seq2seqについて説明しているものを選べ
  - (1) 時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである
  - (2) RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる
  - (3) 構文木などの木構造に対して、隣接単語から表現ベクトル（フレーズ）を作るという演算を再帰的に行い（重みは共通）、文全体の表現ベクトルを得るニューラルネットワークである
  - (4) RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである
- 正解：(2)
  - (1) 双方向RNN
  - (2) Seq2Seq
  - (3) 構文木
  - (4) LSTM
Seq2Seqの課題
- 一問一答しかできない
- 問いに対して文脈もなく、ただ応答が行われ続ける
  - そこで「HRED」の登場です
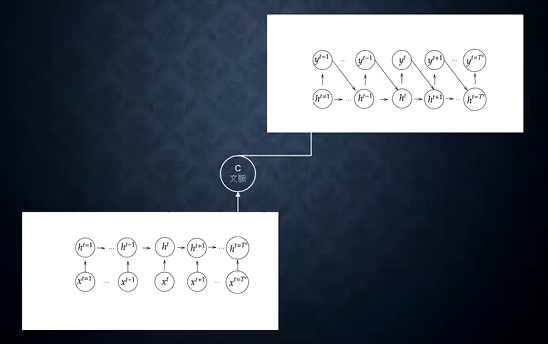
HRED
- 過去n-1個の発話から次の発話を生成する
- Seq2Seqでは、会話の文脈無視で応答がなされるのに対し、HREDでは前の単語の流れに即して応答されるため、より人間らしい文章が生成される
- Seq2Seq + Context RNN
  - Context RNN：Encoderのまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造
  - 過去の発話の履歴を加味して返答できる
- HREDの課題
  - 会話の「流れ」のような多様性がない
  - 情報量に乏しい（短文）答えをしがち
VHRED
- HREDにVAEの潜在変数の概念を追加したもの
- 返答にバリエーションを持たせられるようにする試み
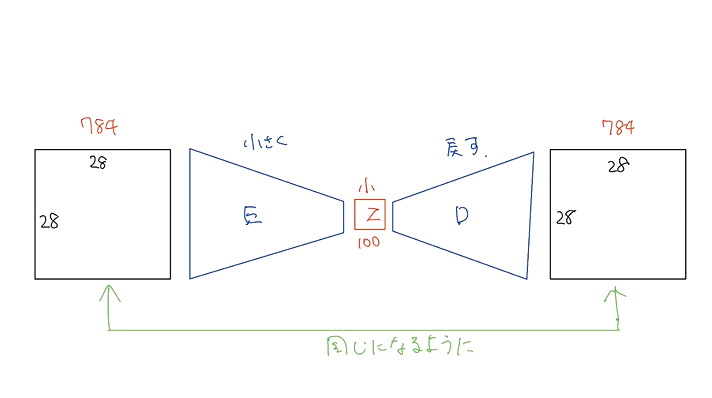
オートエンコーダ
- 教師なし学習の一つ。学習時の入力は訓練データのみで教師データは利用しない
- Encoder-Decoderモデルの一種。
  - Encoder：入力データから潜在変数zに変換するニューラルネットワーク（Decoderが復元しやすいような潜在変数zを作りだす）
  - Decoder：逆に潜在変数zをインプットとして元画像を復元するニューラルネットワーク（潜在変数zからいい感じに復元する）
- メリット
  - 次元削減が行える（zの次元が入力データより小さい場合）

VAE（Variational AutoEncoder）
- zを作り出すときに正則化を行う
  - 通常のオートエンコーダでは潜在変数zの構造に縛りがない（元のデータの類似度が潜在変数zの類似度に近しくなくてもよい）
  - VAEは潜在変数zに確率分布$z \sim N(0,1)$を仮定する
  - VAEはデータを潜在変数zの確率分布という構造に押し込める
  - ノイズを付加することでより汎化性の高いモデルが作成できる
演習問題
- VAEに関する下記の説明文中の空欄に当てはまる言葉をこたえよ
  - 自己符号化器の潜在変数に〇〇〇を導入したもの
  - 解答
    - 確率分布
  - 補足
    - 自己符号化器はオートエンコーダを指す

5-2. 演習

演習なし

6. Word2Vec

6-1. 要点まとめ

Word2Vecとは？
- 単語をベクトル表現にする方法（embedding表現を得る手法の一つ）
- 大規模データの分散表現の学習が現実的な計算速度とメモリ量で実現可能となった
  - ×：ボキャブラリ×ボキャブラリの重み行列が誕生（ほとんどゼロ）
  - 〇：ボキャブラリ×任意の単語ベクトル次元で重み行列が誕生
- 自然言語処理の流れ
  - Word2Vecで小さなベクトル表現に置き換えたのち、Seq2Secに放り込んでタスクを解くなどする

6-2. 演習

演習なし

7. Attention Mechanism

7-1. 要点まとめ

Seq2Seqは長い文章への対応が難しいという問題がある
- 2単語でも、100単語でも、固定次元ベクトルの中に詰め込む必要がある　⇒　長い文の場合に情報が欠落するため、適切に表現できない
解決策
- 重要な単語を自動的に見つけ出す仕組み（Attention Mechanism）
- 文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく仕組み
- 「入力と出力のどの単語が関連しているか」の関連度を学習する仕組み
確認テスト
- RNNとWord2Vec、Seq2SeqとAttentionの違いを簡潔に述べよ
  - RNNとWord2Vec
    - RNNは時系列データを処理するのに適したネットワーク
    - Word2Vecは単語の分散表現ベクトルを得る手法
  - Seq2SeqとAttention
    - Seq2Seqは一つの時系列データから別の時系列データを得るネットワーク
    - Attentionは、時系列データの中身に対して、それぞれの関連性をつけるメカニズム
- Seq2SeqとHRED、HREDとVHREDの違いを簡潔に述べよ
  - Seq2Seqによる応答では会話の文脈が無視されるのに対し、HREDでは前の単語の流れに即して応答される
  - HREDでは文脈に対して当たり障りのない文脈しか作れないのに対し、VHREDでは返答にバリエーションを持たせられるようになった

7-2. 演習

演習なし

8. 強化学習

8-1. 要点まとめ

強化学習とは？
- 学習分類の一つ（教師あり学習、教師なし学習、強化学習）
- 教師あり学習、教師なし学習：データの特徴を見つける
- 強化学習：目的を準備して、目的をうまく解決する方法を見つける

探索と利用のトレードオフ
- 不完全な知識のもとで行動しながら、データを収集。最適な行動を見つけていく
  - 過去のデータでベストとされる行動のみとっていると新たなベストを見つけられない
  - 未知の行動のみをとり続ければ、過去の経験を生かせない
「強化学習」と「教師あり・教師なし学習」の違い
- 目標が異なる
- 教師あり・教師なし学習では、データに含まれるパターンを見つけ出す、およびそのデータから予測することが目標
- 強化学習では、優れた方策を見つけることが目標
強化学習の歴史 ※参考ページ
- 関数近似法とQ学習を組み合わせる手法が登場したことがブレイクスルーとなった
- Q学習
  - 行動価値関数を、行動する毎に更新することにより学習を進める方法
- 関数近似法
  - 価値関数や方策関数を関数近似する手法のこと（この関数にNNを利用する）
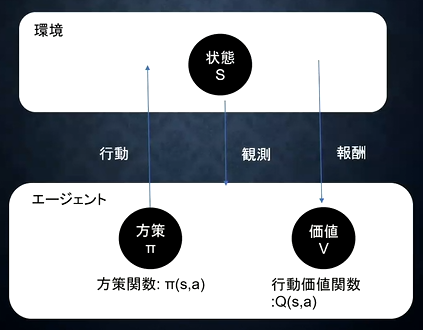
価値関数
- 状態価値関数と行動価値関数の2種類がある
- 状態価値関数
  - 価値を決めるときの決め方。環境の状態だけが価値を決定する
- 行動価値関数
  - 状態とエージェントがとった行動の2つをもとに価値を決定する（Q学習で利用される）
方策関数
- 方策関数の結果をもとに、エージェントの行動が決定される
- ある状態でどのような行動をとるかの確率を与える関数のこと
- 価値関数が出す価値を最大化する行動を決定する
関数の関係
- エージェントは方策に基づいて行動する
- 方策関数：価値関数が最大となるように、今どう行動するか
  - $\pi \left( s \right) = a$
- 価値関数：ゴールまで今の方策を続けたときに、どの程度報酬が得られるか
  - 状態関数：$V^{\pi} \left( s \right)$
  - 状態+行動関数：$\pi \left( s, a \right)$
方策勾配法
- 方策反復法
  - 方策をモデル化して最適化する手法
    - $\theta^{(t+1)} = \theta^{(t)} + \epsilon \nabla J \left( \theta \right)$
    - $J$は方策の期待収益（誤差関数に当たるもの）を表す
    - 「+」になっている
      - 強化学習の場合は、なるべく多くの”報酬”を得る方向に学習を進めるため
  - 定義方法
    - 平均報酬
    - 割引報酬和
  - 上記定義に対応して、行動価値関数：$Q \left( s, a \right)$の定義を行う
  - 方策勾配定理

\nabla_{\theta} J \left( \theta \right) = \mathbb{E}_{\pi_{\theta}} [ ( \nabla_{\theta} \log \pi_{\theta} (a|s) Q^{\pi} (s, a))]

8-2. 演習

演習なし

9. AlphaGo

9-1. 要点まとめ

AlphaGo Lee
- 2代目バージョン。TPU48台を使用
  - 2016年3月、韓国棋界で「魔王」と呼ばれる世界トップ棋士の一人の李世乭 (Lee Sedol) と戦い、4勝1敗と勝ち越した
- PolicyNet：方策関数のCNN
  - 入力データ
    - 19x19（48チャンネル）のデータを入力に取る
      - 19x19：囲碁の盤面
      - 48チャンネル：48種類の情報を持つ
        
        石：自石、敵石、空白の3チャンネル
        
        オール1：前面1　など
  - 出力データ
    - Softmax Layerを通すことで確率分布に変換
    - 19x19の着手予想確率
- ValueNet：価値関数のCNN
  - 入力データ
    - 19x19（49チャンネル）のデータを入力に取る　※PolicyNetより「手番」の1チャネル分多い
  - 出力
    - TanH Layerを通すことで、-∞～∞の値を1～1までに変換する
    - 出力は現局面の勝率を-1～1で表したものが出力される
- PolicyNetの強化学習
  - 「現状のPolicy」vs「PolicyPoolからランダム抽出されたPolicyNet」と対局シミュレーションを行い、その結果を用いて方策勾配法で学習を行う
  - PolicyPoolとはPolicyNetの強化学習の過程を500Iterationごとに記録し保存しておいたもの
  - 過学習を防ぐ目的で、現状のPolicy同士での対局とはしない。
- PolicyNetの教師あり学習
  - KGS Go Server（ネット囲碁対局サイト）の棋譜データから3000万局面分の教師を用意し、教師と同じ着手を予測できるよう学習を行った
  - 教師が着手した手を1とし残りを0とした19x19次元の配列を教師都市、それを分類問題として学習した
  - このPolicyNetは57%程の精度であった
- ValueNetの学習
  - PolicyNetを使用して対局シミュレーションを行い、その結果の勝敗を教師として学習
- RollOutPolicy
  - 計算量の少ない、スピード重視の方策関数。（線形の方策関数）
  - PolicyNetに比べて1000倍速い（PlicyNet:3ミリ秒、RollOutPolicy:3マイクロ秒）
- AlphaGoの学習ステップ
  - 教師あり学習によるRollOutPolicyとPolicyNetの学習
  - 強化学習によるPolicyNetの学習
  - 強化学習によるValueNetの学習
  - ポイント
    - 強化学習は計算量が多く、学習がしづらい。教師あり学習で補った後に強化学習を進める
- モンテカルロ木探索
  - 強化学習の学習手法の一種。
  - 囲碁のように、１手１手進んでいって、最後の盤面で勝敗が付くようなゲームに当てはまりがよい
    - 他のボードゲームでは「minmax探索」や「αβ探索」を使うことが多いが、盤面の価値や勝率予想値が必要となるが、囲碁では困難であった。
    - そこで、盤面評価値に頼らず、末端評価値、つまり勝敗のみを使って探索を行うという発想で生まれた探索法
    - 囲碁の場合、最大手数はマスの数でほぼ限定されるため、末端局面に到達しやすい
    - Alpha Goのモンテカルロ木探索は選択、評価、バックアップ、成長という4つのステップで構成される
AlphaGo LeeとAlphaGo Zeroの違い
- 教師あり学習を使わず、強化学習のみで作成
- 特徴入力からヒューリスティックな要素を排除し、石の配置の身にした（人間が選択した特徴量を排除した）
- PolicyNetとValueNetを1つのネットワークに統合にした
- Residual Netを導入した
- モンテカルロ木探索からRollOutシミュレーションをなくした
AlphaGo ZeroのPolicyValueNet
- 入力は盤面特徴入力1つで、Residual Blockで生成されたデータを、Policy出力とValue出力の2つの出力を生成
- Residual Network
  - ネットワークを深くすると勾配消失問題が起きる。
  - 深さを抑えるためのショートカットを作ることで、勾配の爆発、焼失を抑える
  - ショートカット構造により、層数の違うNetworkのアンサンブル効果が得られる（という説もある）
Residual Networkの派生形
- Residual Blockの工夫
  - Bottleneck
    - 1x1 KernelのConvolutionを利用し、1層目で次元削減を行って3層目で次元を復元する3層構造にし、2層のものと比べて計算量はほぼ同じだが、1層増やせるメリットがある、としたもの
  - PreActivation
    - ResidualBlockの並びをBatchNorm→ReLU→Convolution→BatchNorm→ReLU→Convolution→Addとすることにより性能が上昇したとするもの
- Residual Networkの工夫
  - WideResNet
    - ConvolutionのFilter数をk倍にしたResNet。1倍→k倍xブロック→2*k倍yブロックと段階的に幅を増やしていくのが一般的。
    - Filter数を増やすことにより、浅い層数でも深い層数のものと同等以上の精度となり、またGPUをより効率的に使用できるため学習も早い
  - PyramidNet
    - WideResNetで幅が広がった直後の層に過度の負担がかかり精度を落とす原因になっているとし、段階的にではなく、各層でFilter数を増やしていくResNet
- 【番外】深層学習モデルにおける重要な基本概念（アイディア）
  - 基本的には以下を組み合わせているだけ
    - 畳み込み、プーリング、活性化関数
    - RNN（ネットワークの出力を次のネットワークの入力人する）
    - アテンション
AlphaGo Zeroの学習法
- 自己対局による教師データの作成、学習、ネットワークの更新の3ステップで構成される
  - 教師データの作成
    - モンテカルロ木探索で自己対局を行う
  - 学習
    - 自己対局で作成した教師データを使い学習を行う
  - ネットワークの更新
    - 現状のネットワークと学習後のネットワークとで対局テストを行い、学習後のネットワークの勝率が高かった場合、学習後のネットワークを現状のネットワークとする

9-2. 演習

演習なし

10. 軽量化・高速化技術

10-1. 要点まとめ

アジェンダ
- 高速化：どうやって計算速度を早くするか
  - モデル並列
  - データ並列
  - GPU
- 軽量化：低性能デバイスでもモデルを動かせるようにする
  - 量子化
  - 蒸留
  - プルーニング
分散深層学習とは
- 背景
  - 毎年10倍ずつペースでデータ、モデルが肥大化している ⇔ コンピュータはおおよそ18～24カ月で2倍の性能になる
  - 複数の計算資源を使用し、並列的にニューラルネットを構成することで、効率の良い学習を行いたい
  - データ並列化、モデル並列化、GPUによる高速技術は不可欠である
- データ並列化
  - 親モデルを各ワーカーに子モデルとしてコピー
  - データを分割し、各ワーカーごとに計算させる
  - 各モデルのパラメータの合わせ方
    - 同期型
      - 各ワーカーが計算し終わるのを待ち、全ワーカーの勾配が出たところで勾配の平均を計算し、親モデルのパラメータを更新する
      - その後、更新後のモデルを子モデルとしてコピー
    - 非同期型
      - 各ワーカーはお互いの計算結果を待たず、各子モデルごとに更新を行う
      - 学習が終わった子モデルはパラメータサーバーにPushされる
      - 新たに学習を始めるときは、パラメータサーバーからPopしたモデルに対して学習していく
    - 同期型と非同期型の比較
      - 処理スピードは非同期型の方が早い（待ち時間がない）
      - 非同期型は学習が不安定になりやすい（最新モデルのパラメータを利用できないため） → Stale Gradient Problem
      - 現在の主流は同期型（性能が良いことが多い）
      - 使いどころ
        
        自分たちが準備したサーバーの場合は同期型（全コンピューターを自由に制御できるため）
        
        世界中のスマホを活用する場合は非同期型（同期型はデッキ内）
- モデル並列化
  - 親モデルを各ワーカーに分割し、それぞれのモデルを学習させる。すべてのデータで学習が終わった後で、一つのモデルに復元。
    - モデルが大きいときはモデル並列化を、データが大きいときはデータ並列化をするとよい
    - データ並列化　→　PCを別にする
    - モデル並列化　⇒　同じPCでやる。計算結果を集めるのが難しい（ネットワーク経由すると遅延が発生）
  - モデルのパラメータ数が多いほど、スピードアップの効果も向上する
- GPUによる並列化
  - CPU
    - 高性能なコアが小数
    - 複雑で連続的な処理が得意
  - GPU
    - 比較的低性能なコアが多数（2000-3000コア）
    - 簡単な並列処理が得意
    - ニューラルネットワークの学習は単純な行列演算が多いので、高速化が可能
  - GPGPU（General-purpose on GPU）
    - もともとの使用目的であるグラフィック以外の用途で使用されるGPUの総称
  - GPGPU開発環境
    - CUDA
      - GPU上で並列コンピューティングを行うためのプラットフォーム
      - NVIDIA社が開発しているGPUのみで使用可能
      - Deep Learning用に提供されているので、使いやすい
    - OpenCL
      - オープンな並列コンピューティングのプラットフォーム
      - NVIDIA社以外の会社（Intel、AMD、ARMなど）のGPUからでも使用可能
      - Deep Learning用の計算に特化しているわけではない
軽量化手法
- 量子化（Quantization）
  - コンピュータで小数を表すことを量子化という
  - 巨大なネットワークは協力な演算装置が必要。メモリ使用量も必要
  - パラメータのデータ型の精度を落とす（64bit浮動小数点→32bit浮動小数点など）ことでメモリと演算処理の削減を行う → 精度は悪くなる
  - メリデメ
    - 〇：計算の高速化
      - NVIDIA Tesla V100　単精度(32bit)：15.7 TeraFLOPS、倍精度(64bit)：7.8 TeraFLOPS
      - NVIDIA Tesla P100　単精度(32bit)：9.3 TeraFLOPS、倍精度(64bit)：4.7 TeraFLOPS
    - 〇：省メモリ化
    - ×：精度の低下
      - 少数の有効桁が小さくなるが、実際には問題はない
      - 極端な量子化、例えば1bitを考えると、これは表現力が少なすぎて収束できない　⇒　16bitは必要
- 蒸留
  - 規模の大きなモデルの知識をもとに軽量なモデルを作る
  - 教師モデルと生徒モデル
    - 教師モデル：予測精度の高い、複雑なモデルやアンサンブルされたモデル
    - 生徒モデル：教師モデルをもとに作られる軽量なモデル
  - 教師モデルの重みを固定し、生徒モデルの重みを更新していく　→　教師モデルのもつ制度を引き継ぎながら学習できる
  - 蒸留の利点
    - 少ない学習回数でより精度の良いモデルを作成できる
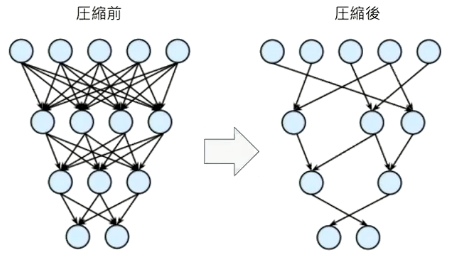
- プルーニング
  - 寄与度の少ないニューロンを削除し、モデルの圧縮を行うことで高速化と省メモリ化できる
  - 重みが閾値以下（例えば0.1など）の場合ニューロンを削減し、再学習を行う

10-2. 演習

演習なし

11. 応用モデル

11-1. 要点まとめ

MobileNets：Efficient Convolutional Neural Networks for Mobile Vision Applications
- 画像認識モデルの軽量化・高速化・高精度化の実現
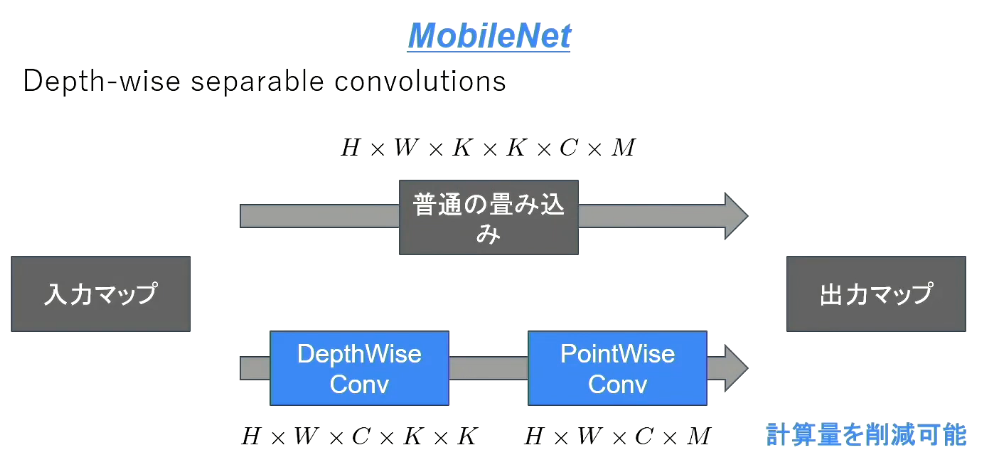
- Depthwise ConvolutionとPointwise Convolutionの組み合わせで軽量化を実現（Depthwise Convolutionの出力をPointowise Convolutionによってチャネル方向に畳み込む）
- 一般的な畳み込みレイヤー
  - 計算量：H × W × K × K × C × M
- Depthwise Convolution
  - フィルタの数は1固定（K × K × 1)
  - 1チャンネルに対して、1つの出力を行う（入力と同じチャンネル数が出力される）
  - 計算量：H × W × K × K × C
- Pointwise Convolution
  - 1x1 convとも呼ばれる（正確には1x1xC）
  - 計算量：H × W × C × M

DenseNet
- 画像認識モデル
- Denseブロック
  - 出力層に前の層の入力を足し合わせる
  - kをネットワークのgrowth rateと呼ぶ。kチャネルずつ増える
- Transition Layer
  - Denseブロックで増えたチャネル数をもとに戻す
- DenseNetとResNetの違い
  - RessidualBlockでは前1層の入力のみ後方へ入力
  - DenseBlockでは成長率（Growth Rate）と呼ばれるハイパーパラメータが存在。kを成長率と呼ぶ
正規化
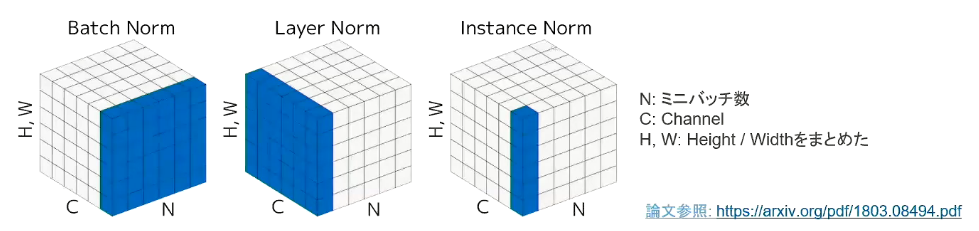
- Batch Norm
  - レイヤー間を流れるデータの分布を、ミニバッチ単位で平均0、分散1に正規化
  - バッチサイズに影響を受ける。マシンによりバッチサイズを変えないといけない
  - バッチサイズが小さいと、学習が収束しないことがある　→　Layer Normalizationなどの手法がある
- Layer Norm
  - それぞれのsampleのすべてのpixels（1つの画像の全チャネルをまとめて）が同一分布に従うよう正規化
    - 入力データのスケールに関してロバスト
    - 重み行列のスケールやシフトに関してロバスト
- Instance Norm
  - さらにchannelも同一分布に従うよう正規化
    - Batch Normalizationのバッチサイズが1の場合と等価
  - コントラストの正規化に寄与・画像のスタイル転送やテクスチャ合成タスクなどで利用

Wavenet
- Aaron van den Oord et. al.,2016らにより提案
- 音声波形を認識するモデル
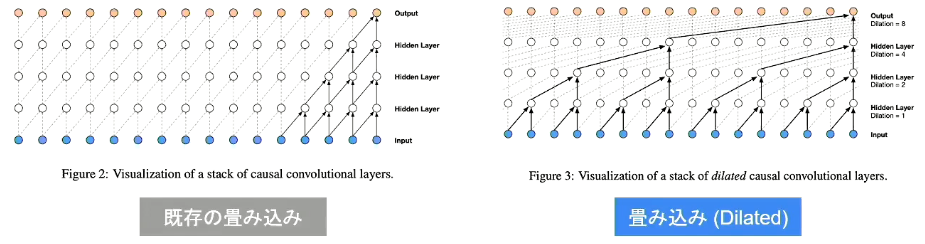
- 時系列データに対して畳み込み（Dilated convolution）を適用する
- Dilated Convolution
  - 層が深くになるにつれて畳み込むリンクを離す
  - 受容野を簡単に増やすことができるという利点がある（パラメータ数は同じで広い範囲の時間を捉える）

【参考】Deconvolution
- 通常畳み込みでは出力サイズは小さくなるが、逆に出力サイズを大きくする
- 例）昔の不鮮明な画像を、鮮明な画像にする

11-2. 演習

演習なし

12. Transformer

12-1. 要点まとめ

Seq2Seqの理解に必要な材料
- RNNの理解
  - RNNの動作原理
  - LSTMなどの改良版RNNの理解
- 言語モデルの理解
  - 単語の並びに確率を与える　単語の並びに対する尤度
  - 時刻t-1までの情報で、時刻tの事後確率を求めることが目標
Seq2Seq
- EncoderからDecoderに渡される内部状態ベクトルが鍵
- Decoder側の構造は言語モデルRNNとほぼ同じだが、隠れ状態の初期値にEncoder側の内部状態を受け取る点が異なる
- Decoderのoutput側に正解をあてれば教師あり学習がEnd2Endで行える
BERTを理解するために必要な材料
- Encoder-Decoder Model
- Transformer（Encoder-Decoder x Attention）
- BERT
ニューラル機械翻訳の問題点
- 長さに弱い　→　翻訳元の文の内容をひとつのベクトルで表現するため、文が長くなると表現力が足りなくなる
- 対応するために、Attention（注意機構）が生まれた
  - 何に注意を払うべきか、何に注意を払わないべきか
  - Attentionは辞書オブジェクト　3要素：query、key、value
    - query(検索クエリ)に一致するkeyを索引し、対応するvalueを取り出す操作であると見做すことができる。
    - これは辞書オブジェクトの機能と同じである
Transformer
- Attention is all you need
  - RNNを使わない。必要なのはAttentionだけ
  - 当時のSOTAをはるかに少ない計算量で実現
- 注意機構には二種類ある
  - Source Target Attention
  - Self-Attention
    - Q/K/Vがすべて同じ場所からくる
    - 入力をすべて同じにして学習的に注意箇所を決めていく
    - CNNに似ている。周辺情報から抽象表現を得る
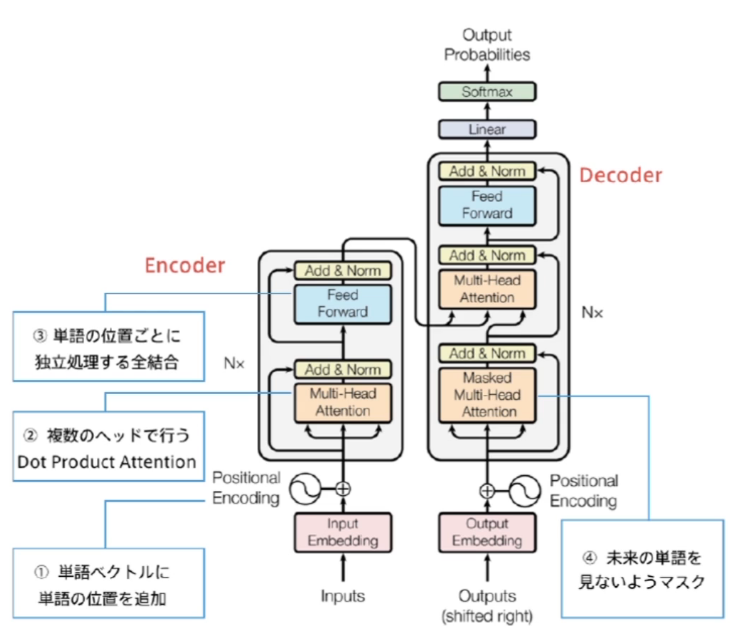
- Position-Wise Feed-Forward Networks
  - 位置情報を保持したまま純伝播させる
- Scaled dot product attention
  - 全単語に関するAttentionをまとめて計算する
- Multi-Head attention
  - 8個のScaled dot product attentionの出力をConcat
  - それぞれのヘッドが異なる種類の情報を収集（それぞれのヘッドが全く異なる注意の掛け方をしている）
- Decoder
  - 各層で二種類の注意機構（Self AttentionとSource Target Attentionの二種類）
  - 自己注意機構
    - 生成単語列の情報を収集
    - 未来の情報をみないようにマスク
  - Encoder-Decoder attention
    - 入力文の情報を収集
    - Encoderの出力へのアテンション
  - Add（Residual Connection）
    - 入出力の差分を学習させる
    - 実装上は出力に入力をそのまま加算するだけ
    - 効果：学習・テストエラーの提言
  - Norm（Layer Normalization）
    - 各層においてバイアスを除く活性化関数への入力を平均0、分散1に正則化
    - 効果：学習の高速化
- Positional Encoding
  - RNNを用いないので単語列の語順情報を追加する必要がある

12-2. 演習

①-0 Seq2Seqによる学習実行の前準備
- 提供されたソースコードそのまま実行するとエラーが発生
- pytorch関連ライブラリのバージョンに起因するものと思われる → 試行錯誤の末以下のようにバージョン指定でインストールして解決

pip install torch==1.7.1+cu92 torchvision==0.8.2+cu92 torchaudio==0.7.2 -f https://download.pytorch.org/whl/torch_stable.html

①-1 Seq2Seqによる学習実行
①-2 モデルを使って翻訳実行
- 意味不明な文章も生成されたが、なんとなくできているのはすごい

①-3 BLEU計算

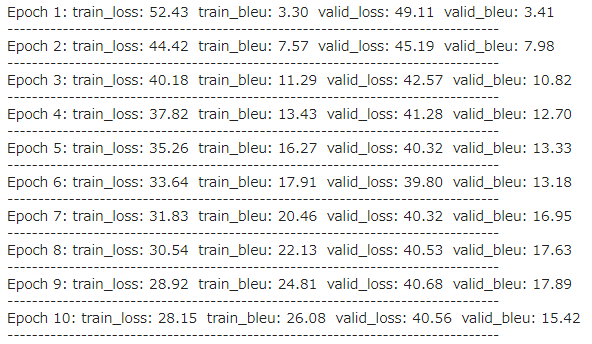
②-1 Transformerによる学習実行
- 15epocでSeq2Seqより早く学習が完了。

②-2 モデルを使って翻訳実行
- 明らかに精度が向上している。中には完全に正解と一致しているものも。

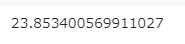
②-3 BLEU計算
- Seq2Seqよりも少し高い程度。性能は歴然に思えたが・・

13. 物体検知・セグメンテテーション

13-1. 要点まとめ

Introduction
- 入力は画像（カラー、モノクロは問わない）
- 出力は分かれる
  - 分類　Classification
    - （画像に対し、単一または複数の）クラスラベル
      - 物体の位置に興味なし！
  - 物体検知　Object Detection
    - Bounding Box [bbox/BB]　物体の検出位置
      - インスタンス（個々の物体）の区別に興味なし！
  - 意味領域分割　Semantic Segmentation
    - （各ピクセルに対し単一の）クラスラベル
      - インスタンス（個々の物体）の区別に興味なし！
  - 個体領域分割 Instance Segmentation
    - （各ピクセルに対し単一の）クラスラベル
代表的なデータセット
- 共通的に精度評価が可能なデータセットが必要になる
- 物体検出コンペティションで用いられたデータセット
- 目的に応じたBox/画像を選択を！
  - 小：アイコン的な移り
  - 大：日常に近い
- クラス数が大きいことはうれしいのか？
  - 同じものだが、別ラベルに設定されているものもある

	クラス	Train+Val	Box/画像	画像サイズ	備考
VOC12	20	11,540	2.4	470x380	PASCAL VOC Object Detection Challenge VOC=Visual Object Classes Instance Annotation(物体毎にラベルが与えられている）
ILSVRC17	200	476,668	1.1	500x400	ILSVRC Object Detection Challenge ILSVRC=ImageNet Scale Visual Recognition Challenge ImageNetのサブセット
MS COCO18	80	123,287	7.3	640x480	MS COCO Object Detection Challenge COCO=Common Object in Context 物体位置推定に対する新たな評価指標を提案 Instance Annotation
OICOD18	500	1,743,042	7.0	一様でない	Open Images Challenge Object Detection ILSVRCやMS COCOとは異なるannotation process Open Images V4（6000クラス以上/900万枚以上）のサブセット Instance Annotation

評価指標
- 復習
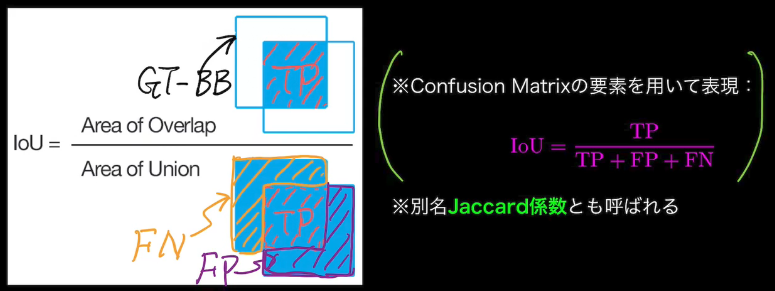
  - 参考：Confusion Matrixと関連指標のおさらい
    - Accuracy/Recall/Precisionってややこしくない??
  - Accuracy（正答率）：(TP+TN)/(TP+TN+FP+FN)
  - Recall（再現率）：TP/(TP+FN)
  - Precision（適合率）：TP/(TP+FP)
  - Precision-Recall curve：confidenceの閾値を変化させることでPR曲線が描ける
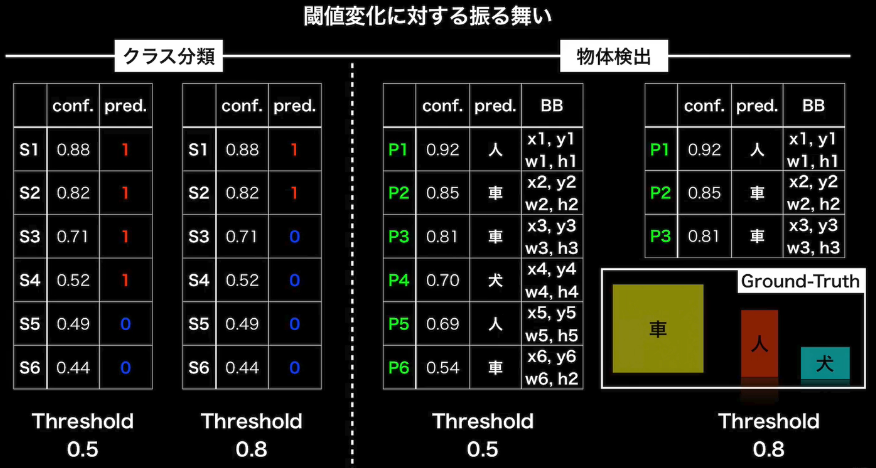
- 閾値変化に対する振る舞い
  - 物体検出の場合は閾値によってConfusion Matrixに当てはめる母数が変わってくる
- IoU：Intersection　Over Union
  - 物体検出においてはクラスラベルだけでなく、物体位置の予測精度も評価したい！

AP：Average Precision
- IoUは0.5に固定して、conf.を変動させる
- PR曲線の下側面積 $AP = \int_{0}^{1} P(R)dR$
- クラスラベル毎に計算して、全クラスの算術平均をとる　$mAP=\frac{1}{C} \sum_{i=1}^{C} AP_i$
- おまけ：MS COCOで導入された指標
  - IoU閾値を0.5から0.95まで0.05刻みでAP＆mAPを計算し算術平均を計算　→　位置の精度を厳しく見ている
    - $mAP_{coco} = \frac{mAP_{0.5}+mAP_{0.55}+ \cdots +mAP_{0.95}}{10}$
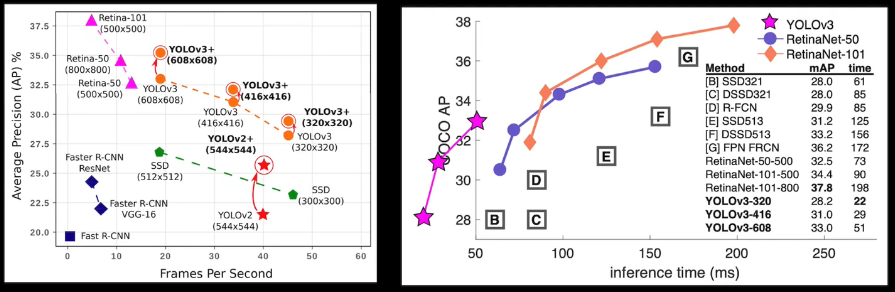
FPS：Flames per Second
- 応用上の要請から、検出精度に加え検出速度も問題となる

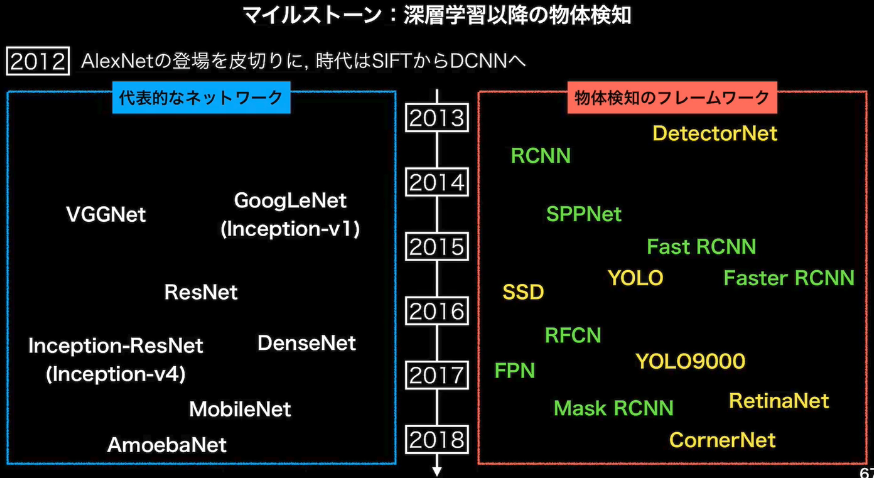
マイルストーン

物体検知のフレームワーク
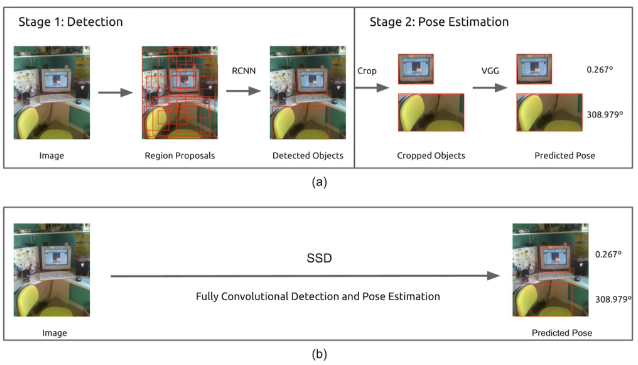
- 2段階検出器
  - 候補領域の検出とクラス推定を別々に行う
  - 相対的に精度が高い傾向
  - 相対的に計算量が大きく推論も遅い傾向
- 1段階検出器
  - 候補領域の検出とクラス推定を同時に行う
  - 相対的に精度が低い傾向
  - 相対的に計算量が小さく推論も早い傾向

SSD：Single Shot Detector
- Default BOXを用意する
- Default BOXを変形し、conf.を出力
- SSDでは、VGG16をベースネットワークとしている
- マルチスケール特徴マップ
  - 検出物体の大きさに合わせてどの特徴マップで対応するかが決まる
    - 小さい物体　→　38x38など解像度が高い特徴マップでとらえる
    - 大きな物体　→　3x3、1x1など解像度が低い特徴マップでとらえる
- 多数のDefault Boxによる問題と対処
  - Non-Maximum Suppression
    - 物体数に対して冗長なDefulault Box
    - IoUの閾値0.3を超えているものの中でConf.が最大となるものに限定　※IoUが0.3以下のものは重なりが少ない＝別の物体を検出していると考える
    - アスペクト比の選定工夫
  - Hard Negative Mining
    - 背景と非背景のそれぞれに割り当てられる数が不均衡になる
    - PositiveとNegativeの比を1:3までとし、不要なNegativeを削る
- 損失関数
  - 「confidenceに対する損失」と「検出位置に対する損失」の両方が考慮されている
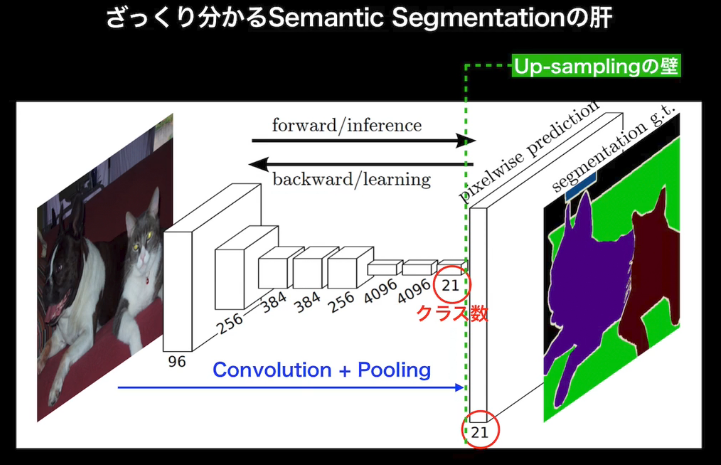
Semantic Segmentation
- 無邪気すぎる疑問：Up-samplingなんて面倒なことが必要になるなら、そもそもPoolingしなければよいのでは？
  - 正しく認識するためには「受容野」にある程度の大きさが必要
  - 受容野を広げる典型
    - ①深いConv.層　→　多層化に伴う演算量・メモリの問題
    - ②プーリング＋ストライド

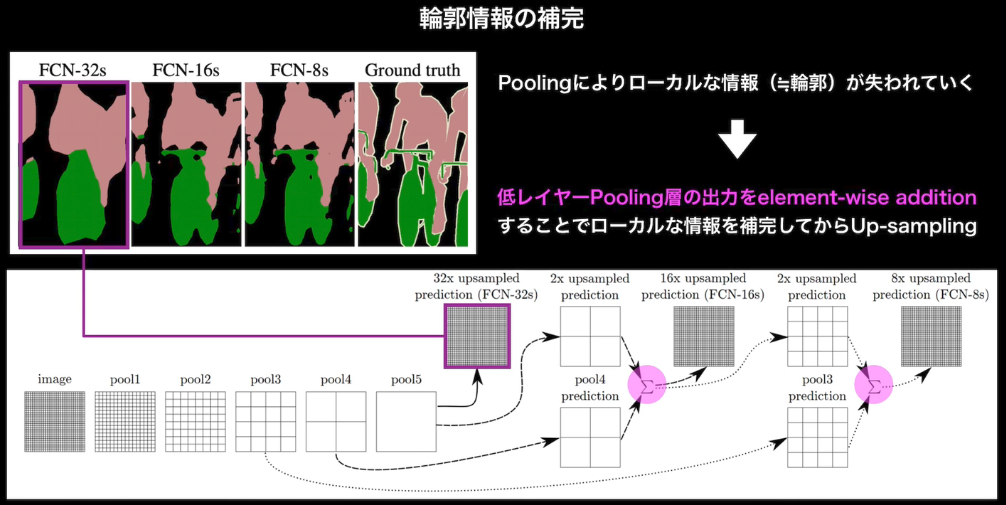
FCN（Fully Convolutional Network）の基本アイディア
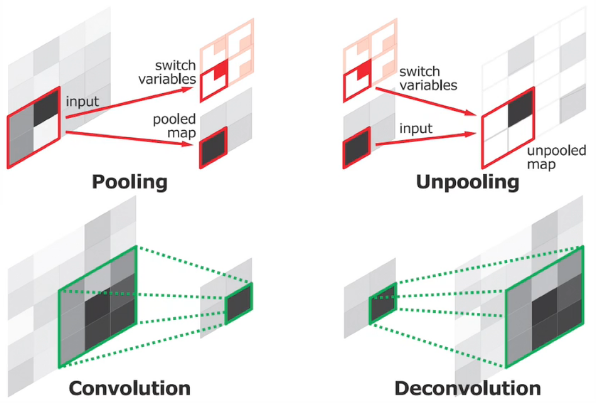
- Deconvolution/Transposed convolution
  - 通常のConv.層と同様、kernel size、padding、strideを指定
  - 処理手順
    - 特徴マップのpixel間隔をstrideだけ空ける
    - 特徴マップのまわりに（kernel size - 1） - paddingだけ余白を作る
    - 畳み込み演算を行う
  - 注意点
    - 畳み込みの逆演算でない
    - poolingで失われた情報が復元されるわけではない

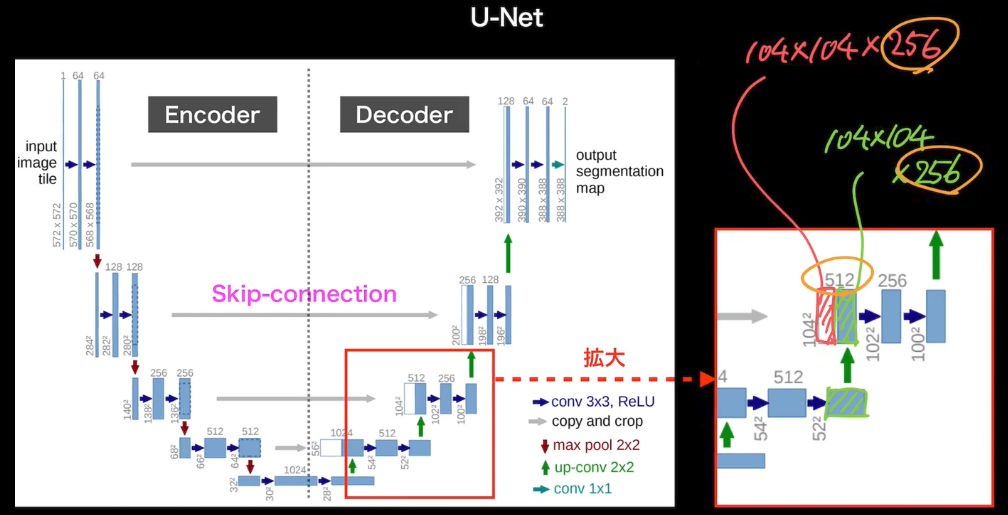
U-Net
- FCNとの違いとして、合算値ではなく、チャネル方向の追加となっている点に注意

Unpooling
- Pooling時の入力情報を保持しておく。戻すときに、最大値の位置を使って戻す

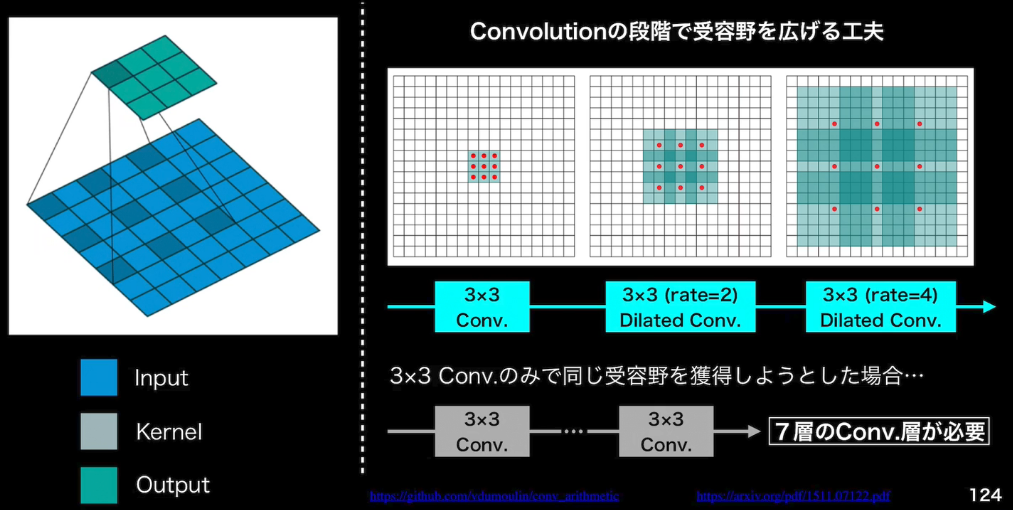
Dilated Convolution
- Convolutionの段階で受容野を広げる工夫
- 3x3 Conv.のみで同じ受容野を獲得しようとした場合、7層のConv.層が必要

13-2. 演習

演習なし

14. DCGAN

14-1. 要点まとめ

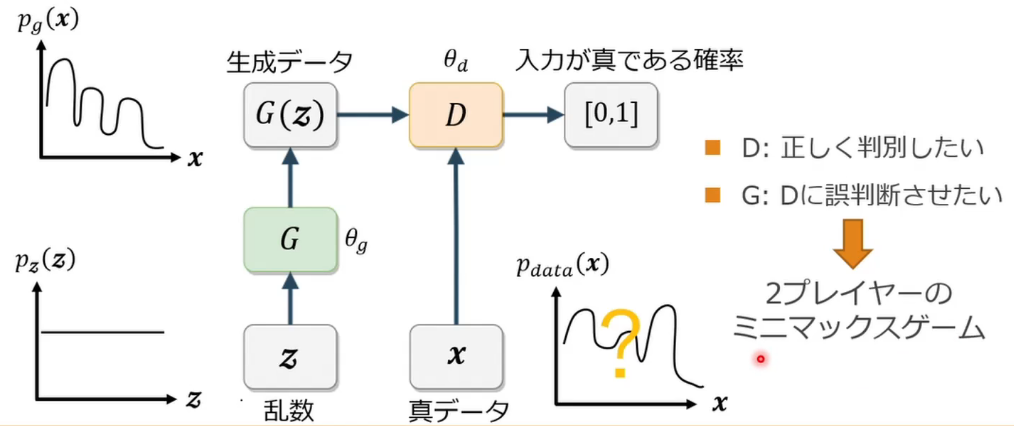
GAN（Generative Adversarial Nets）とは？
- 生成器と識別機を競わせて学習する生成＆識別モデル
  - Generator　乱数からデータを生成
  - Discriminator　入力データが真データ（学習データ）であるかを識別

2プレイヤーのミニマックスゲームとは？
- 一人が自分の勝利する確率を最大化する作戦をとる
- もう一人は相手が勝利する確率を最小化する作戦をとる
- GANでは価値観数Vに対して、Dが最大化、Gが最小化を行う → バイナリークロスエントロピーと似ている？

最適化方法
- GeneratorとDiscriminatorの2種類を更新する必要がある
- Discriminator
  - Generatorのパラメータ$\theta_g$を固定
  - 真データと生成データをm個ずつサンプル
  - $\theta_d$を勾配上昇方（Gradient Ascent）で更新　※Discriminatorは、価値関数の価値を最大化させるため
- Generator
  - Discriminatorのパラメータ$\theta_d$を固定
  - 生成データをm個ずつサンプル
  - $\theta_g$を勾配降下法（Gradient Descent）で更新 ※Generatorは、価値関数の価値を最小化させるため
生成データが本物とそっくりな状況とは？
- $P_g = P_{data}$であるはず　→　本物と同じ分布のデータを生成できる
- 価値観数が$P_g = P_{data}$の時に最適化されていることを示せればよい
- 二つのステップにより確認する
  - Gを固定し、価値関数が最大値を撮るときのD(x)を算出
  - 上記のD(x)を価値関数に代入し、Gが価値関数を最小化する条件を算出
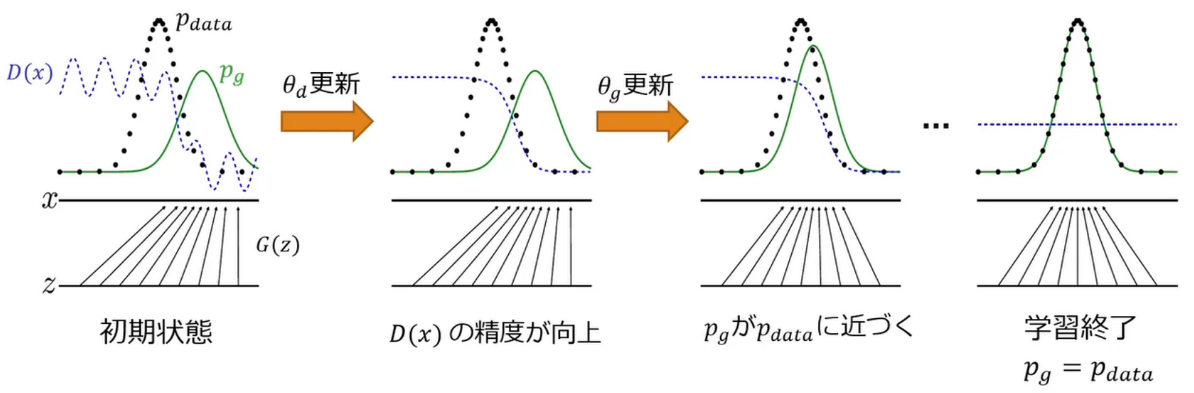
学習ステップの可視化

DCGAN（Deep Convolutional GAN）とは？
- GANを利用した画像生成モデル
- いくつかの構造制約により生成品質を向上
- Generator
  - Pooling層の代わりに転置畳み込み層を使用　※転置畳み込み層の名前は文献により違うケースあり
  - 最終層にtanh（最終出力はとりえる値の範囲を0～1に収めたいため）、その他はReLU関数で活性化
- Discriminator
  - Pooling層の代わりに畳み込み層を使用
  - Leaky ReLU関数で活性化
- 共通事項
  - 中間層に全結合層を使わない（より長いネットワークにしていくためのコツ）
  - バッチノーマライゼーションを適用
応用技術
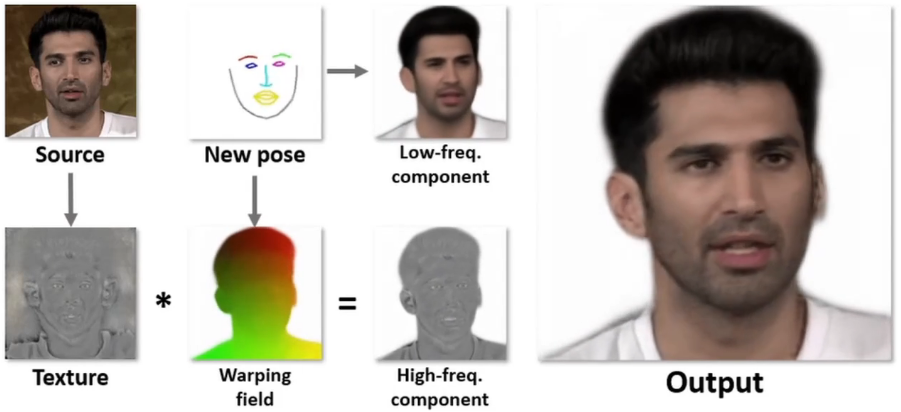
- Fast Bi-layer Neural Synthesis of One-Shot Realistic Head Avatars
- 1枚の顔画像から動画像（Avatar）を高速に生成するモデル
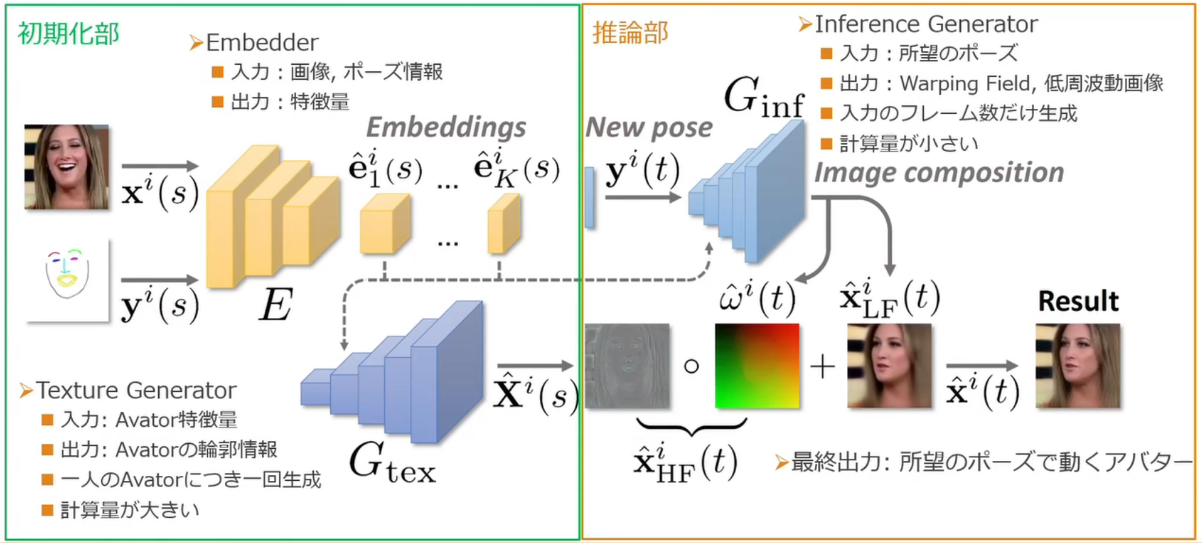
- 初期化部と推論部からなる
- 計算コストの比較
  - 従来：初期化の計算コスト＝小、推論部の計算コスト：大
  - 提案：初期化の計算コスト＝大、推論部の計算コスト：小　→　リアルタイムで推論できる
- 推論部の計算コスト削減方法
  - 緻密な輪郭と粗い顔画像を別々に生成し結合する
    - 初期化時に輪郭情報を生成（ポーズに非依存）
    - 推論時に粗い動画像を生成（ポーズに依存）

ネットワーク構造

14-2. 演習

演習なし

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

JDLA E資格検定メモ 深層学習2

目次

0. 初めに

1. 再起型ニューラルネットワークの概念

1-1. 要点まとめ

1-2. 演習

2. LSTM

2-1. 要点まとめ

2-2. 演習

3. GRU

3-1. 要点まとめ

3-2. 演習

4. 双方向RNN

4-1. 要点まとめ

4-2. 演習

5. Seq2Seq

5-1. 要点まとめ

5-2. 演習

6. Word2Vec

6-1. 要点まとめ

6-2. 演習

7. Attention Mechanism

7-1. 要点まとめ

7-2. 演習

8. 強化学習

8-1. 要点まとめ

8-2. 演習

9. AlphaGo

9-1. 要点まとめ

9-2. 演習

10. 軽量化・高速化技術

10-1. 要点まとめ

10-2. 演習

11. 応用モデル

11-1. 要点まとめ

11-2. 演習

12. Transformer

12-1. 要点まとめ

12-2. 演習

13. 物体検知・セグメンテテーション

13-1. 要点まとめ

13-2. 演習

14. DCGAN

14-1. 要点まとめ

14-2. 演習

JDLA E資格検定メモ深層学習2