自作ラムダ計算処理系「らむだフレンズ」

初のQiita投稿でアドベントカレンダーに参加する勇気。

(2021/11/29) 現状に合わせてちょっと改訂。
(2023/08/22) 独自ドメイン（nikosai.ml）を喪失したのでリンク先をgithub.ioに変更

ラムダ計算とは

ChurchとKleeneが提唱した計算モデルで、無名の関数のみによってあらゆる計算を表現する試みです。関数型プログラミング言語の理論的基盤としても有名ですね。Church-Turingの定立によれば、「計算可能関数」をすべて計算できる（チューリング完全）ことになっています。

ちなみにChurchは、TuringとKleeneの博士課程指導教員だったそうです。離散数学分野ではいずれもよく見る名前ですね。

ここでは、普通のラムダ計算を知っていることを前提にします。

（本当はもっと詳細なラムダ計算の解説を書いていたのですが、あまりに長くなりすぎたのでボツにしました。そのうち別記事にするかも。ラムダ計算について知りたい人は本ページ最後のリンク集を参考に。）

らむだフレンズとは

型なしラムダ計算の高機能な自作インタプリタです。TypeScriptで書かれているので、当然Webブラウザ上でも動作します。スマホからでさえ。

Web（GUI）版らむだフレンズはこちらから

「ラムダ計算のインタプリタなんて、TAPLを読んだ人だったら大体書いてるでしょ」とお思いの方も多いと思います。でも、以下のような機能をすべてサポートした強力なインタプリタはそうそうないでしょう。

• Webページ上でスタンドアロンに動作する（クライアント側のみで完結する）
• マクロ機能がある（組み込み＆ユーザー定義）
• SKIコンビネータとの相互変換ができる
• 評価戦略を自由に選択できる
• 簡約過程を $\LaTeX$ で出力できる
• GUI/CLIの双方で動作する（ワンライナー実行も可能！）

以下では、Web（GUI）版を例に、主な機能を順に紹介します。

入力形式

構文はいわゆる教科書的な“ラムダ計算”と一緒です。

  M ::= x \mid (M \ M) \mid (\lambda x.M)

ただし、入力に当たっては以下の注意点があります。

• \ ¥ λ はすべてラムダとして解釈される
• 関数適用は左結合的に解釈される
• ラムダ抽象は最長一致で解釈される
• 以上2つをもって曖昧性が排除される場合、括弧は省略して良い
• 空白文字は無視される
• 変数に使用できるのは [a-zA-Z]（大小英文字1字,計52文字）のみ

例えば、$\lambda x.x$ を \x.x あるいは λx.x などと書きます。$\lambda xy.x$ は \xy.x 。

変数名を1文字に限っているので、空白は入れても入れなくても意味は変わりません。

基本機能（「出力」タブ）

画面上部のボックスにお好みのラムダ式を入力し、送信ボタン（またはEnterキー）を叩くと、次のような表示が出てきます。

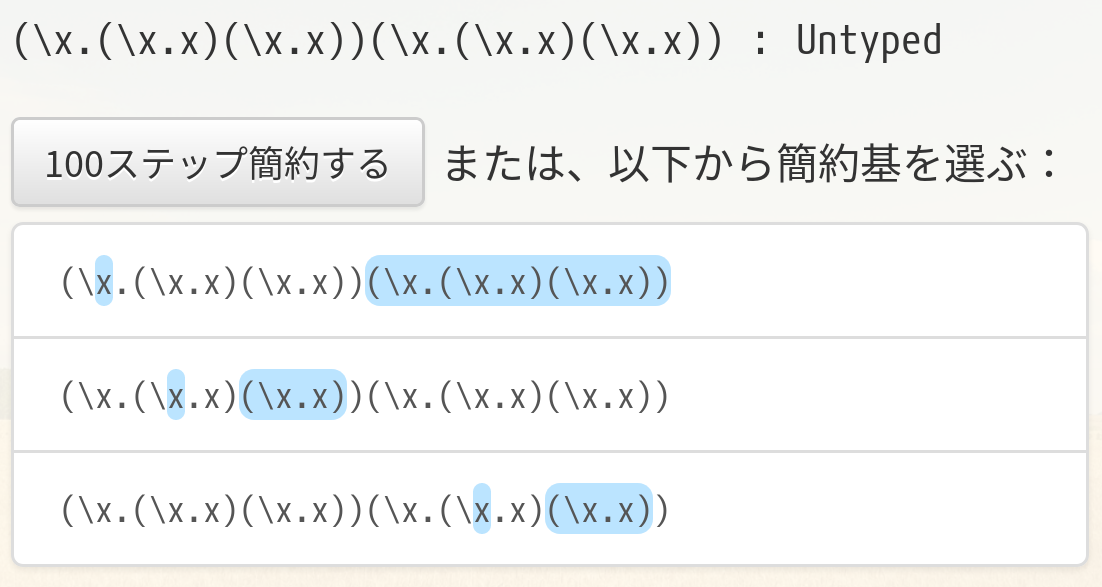
「100ステップ簡約する」ボタン（または入力ボックス上でEnterキー）を押すと、設定されたステップ数（デフォルトでは100）だけ連続して簡約を行います。

あるいは、表示されている候補から簡約基を選んで簡約することもできます（完全β簡約）。β簡約は勿論、η簡約にも対応しています（設定によりON/OFF可能）。

簡約後の形がチャーチ数やチャーチ真理値になっている場合は、その旨を表示します。

また、入力ボックス上で方向キーの を押すと、Bash等のように入力履歴を参照できます。もちろん、静的javascriptなので、セッションを超えて遡ることはできません。

追記： 評価戦略の指定について（2018/12/09）

連続して簡約を行う場合、用いる評価戦略を指定することができます。デフォルトでは最左最外（強）簡約を採用します。

• 最左・最右簡約（leftmost / rightmost）
  • 最左簡約では関数適用の左の子から探索し、最右簡約では右の子から探索する。
• 最外・最内簡約（outermost / innermost）
  • 最外簡約では先行順深さ優先で探索を行うが、最内簡約では後行順深さ優先で探索を行う。
• 強・弱簡約（strong / weak）
  • 強簡約ではラムダ抽象の内部（本体）を簡約するが、弱簡約では簡約しない。
• 頭部簡約（冠頭簡約, head）
  • 頭部簡約では、連続する関数適用の最左のみを簡約する。つまり、関数適用の最左の子が関数抽象である場合のみ、その関数抽象の簡約が許される（最左・最右の設定は無視される）。

ちなみに、最左最外簡約ではβ標準形が、弱頭部簡約では弱頭部標準形が、頭部簡約では頭部標準形が出てきます。

マクロ機能

ユーザー定義マクロ（「マクロ」タブ）

Y = \f.(\x.f(xx))(\x.f(xx)) のように書いて送信することでマクロを定義することができます。

定義したマクロは、 <Y> のように書くと使用できます。

未定義のマクロが式中に現れた場合は、自由変数と同様に扱われます（簡約基とみなされない）。

マクロ定義ファイル（「マクロ」タブ）

「ファイル読み込み」ボタンから、マクロ定義を書き並べたテキストファイルを読み込ませることができます。

macro.txt

# Arithmetic operators on Church numerals
succ   = \n.\sz.s(nsz)
add    = \mn.\sz.ms(nsz)
sub    = \mn.n<pre>m
mul    = \mn.\sz.m(ns)z
exp = \mn.nm

これらの他にも、基本的なラムダ式を書き並べたサンプルを用意してありますのでご活用ください。
ちなみに、「ファイル読み込み」ボタン右側の▼から「サンプルファイルを読み込み」で直接上記サンプルファイルを読み込むこともできます。

組み込みマクロ

以下の3つは、ユーザが定義しなくても利用できます。ただし、ユーザ定義のマクロによって上書きされるので注意。

• チャーチ数： <3> <5> など
• チャーチ真理値： <true> <false>
• SKIコンビネータ： <S> <K> <I>

つまり、単に <2><2> と書けば $2^2$ が計算できます。

各種変換・出力機能

入力されたラムダ式からの変換・出力（「Export」タブ）

• ここまでの簡約過程を$\LaTeX$で出力する

\begin{eqnarray*}
&& (\strut \lambda{\underline{f}}x.f(fx))\underline{\strut (\lambda fx.f(fx))} \\
&\longrightarrow_{\beta}& \lambda{x}.(\strut \lambda{\underline{f}}x.f(fx))\underline{\strut ((\lambda fx.f(fx))x)} \\
&\longrightarrow_{\beta}& \lambda{xa}.(\strut \lambda{\underline{f}}x.f(fx))\underline{\strut x}((\lambda fx.f(fx))xa) \\
&\longrightarrow_{\beta}& \lambda{xa}.(\strut \lambda{\underline{a}}.x(xa))\underline{\strut ((\lambda fx.f(fx))xa)} \\
&\longrightarrow_{\beta}& \lambda{xa}.x(x((\strut \lambda{\underline{f}}x.f(fx))\underline{\strut x}a)) \\
&\longrightarrow_{\beta}& \lambda{xa}.x(x((\strut \lambda{\underline{a}}.x(xa))\underline{\strut a})) \\
&\longrightarrow_{\beta}& \lambda xa.x(x(x(xa)))\not\longrightarrow
\end{eqnarray*}

• deBrujinインデックスに変換する
  • ex. \fx.f(fx) → \ \ 1 (1 0)
• SKIコンビネータに変換する
  • ex. \fx.f(fx) → <S>(<S>(<K><S>)(<S>(<K><K>)<I>))(<S>(<S>(<K><S>)(<S>(<K><K>)<I>))(<K><I>))
• 階層グラフ書換え言語LMNtalに変換する

ラムダ式への変換（「Import」タブ）

• deBrujinインデックスからラムダ式への変換
• LMNtalコードからラムダ式への変換
• 与えられた形の簡約グラフを生成するようなラムダ式を逆引きする
  • 実験中につき不完全だが健全性は満たしているはず

ちなみにSKIコンビネータ→ラムダ式の変換は組み込みマクロを使用することで可能です。

簡約グラフ表示（「グラフ」タブ）

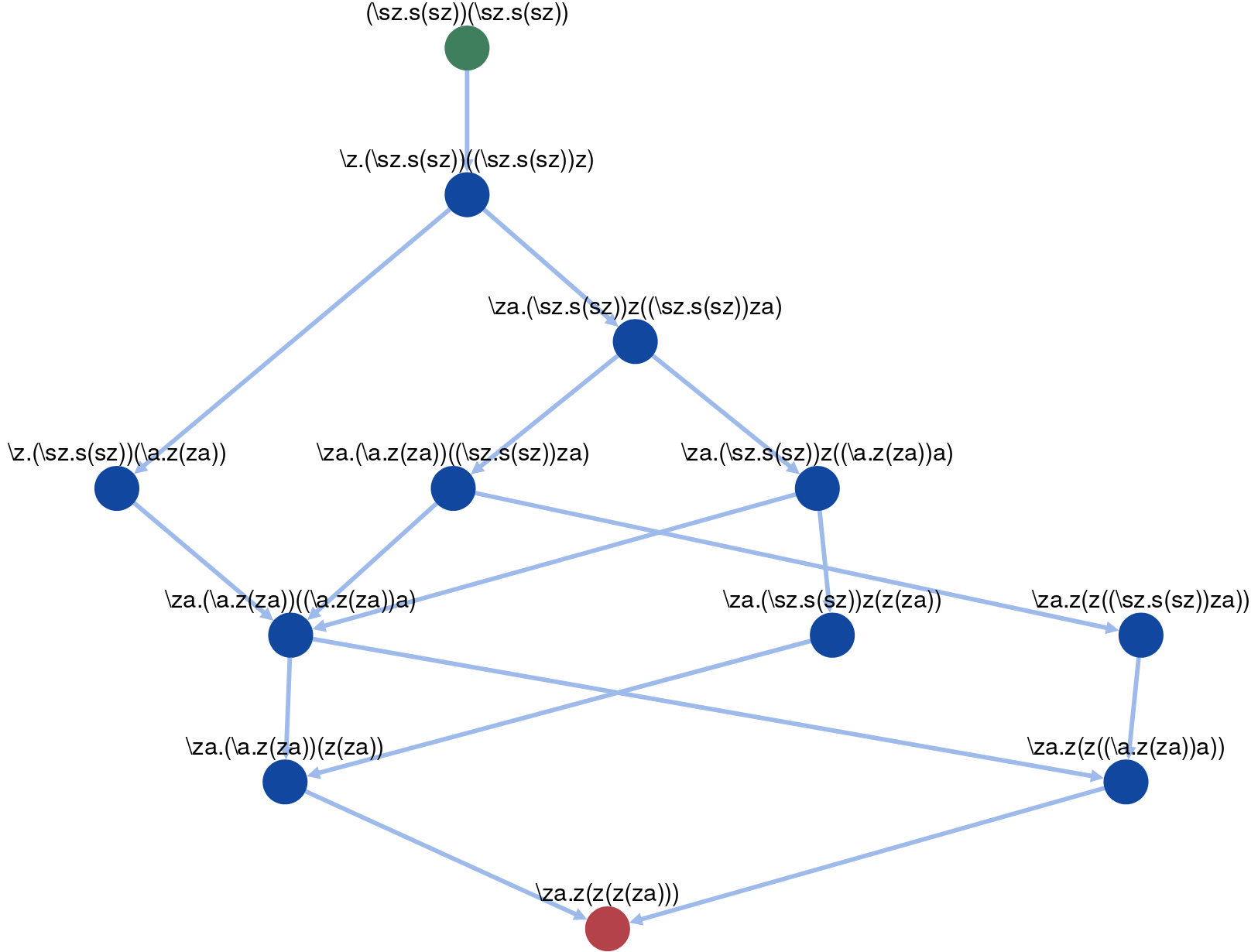
非決定的に簡約を行った場合にどのような簡約が有りうるかを有向グラフとして表示することができます。これを簡約グラフと呼んでいます。

ラムダ式が入力された状態で「Start」ボタンを押すと、指定の深さ（デフォルトでは10）まで幅優先に探索を行い、Cytoscape.jsによりグラフとして表示します。

上図はチャーチ数の $2^2$ です。得られたグラフは「PNG」ボタンでpng画像としてダウンロードできます。

ちなみに多重辺のON/OFFも切り替えられます。多重辺をもつラムダ式には例えば (\x.x)((\x.x)(\x.x)) などがありますね。

CLIモードの動かし方

必須環境： Node.js・TypeScript（できれば最新のもの）

インストール方法

$ git clone https://github.com/nikosai/lambda-friends.git
$ cd lambda-friends
$ npm i

REPLの起動

$ ./run.sh

詳しい操作説明はここでは割愛します。:? または :h で表示されるヘルプを参照してください。

また、実行時オプションを付けることもできます。使用できるオプションは、./run.sh -hで表示されます。

特に、./run.sh -i "<2><2>" のようにすると、ワンライナーで実行ができます。

型付きモード（β）

まだβ版なので表向きは出していませんが、「単純型付きラムダ計算」モードもあり、ML系のミニ関数型言語が一応動作します。字句解析をサボっているのでキーワードに全部角括弧を付す必要があって読みづらいことこの上ありませんが……。

簡単な型推論を行うことができ、その証明図を$\LaTeX$形式（要bussproofs.sty）で出力できます。使い方について詳しくは下記GitHubのREADMEを参照してください。

その他細かいところ

• コード量は現在4000行前後、独力での開発です。
• Web版は、TypeScript＋webpackでjsファイルに変換し、GitHub Pages上で動作させています。
• CLI版は、Node.jsで動作します。
• 簡約グラフの表示機能などごく一部を除き、フルスクラッチでの開発（パーサジェネレータ等は不使用）
• GitHubでコードを公開しています（MITライセンス）。より技術的な詳細はこちらをご覧ください。
• このプロジェクトは、Lambda*Magicaに影響を受けて始動しました。
• ロゴは、けものフレンズ ロゴジェネレータで作成しました。

お問い合わせ

個人Webサイト

役立つリンク集

• Wikipedia「ラムダ計算」
  • この辺の分野では英語版Wikipediaの方が役に立つことが多い
  • 英語版Wikipedia「Lambda Calculus Definition」 ← 「大半の人には難解だから整理しろ」というテンプレートが張ってありますので、整理される前にぜひ。
• ラムダ計算の解説YouTube動画（英語）
• 「ラムダ計算」を独学で学習するための，講義ノートやPDFのリンク集
• 書籍なら、オススメは……
  • 萩谷・西崎著「論理と計算のしくみ」
  • 「Types and Programming Languages（TAPL）」
  • 「型システム入門 プログラミング言語と型の理論」（TAPLの訳書）