動機
- 最も大事な動機としては、単に数学を久しぶりにやりたかった。ただそれだけ。
- 学生時代に勉強したのに結構ブランクあるので、リハビリもかね興味あるものを取り上げた。
- qiitaで書く理由は、Haskellなどプログラミングへ応用されているので、書く場所として的外れでないから。
- 例えばカリー化とかを圏論の言葉で説明されることもあったりする。そういうときに理解できるようにしておきたい
- あと、qiitaで数式を書いたことがないので、試したい、というのもある。
執筆のスタイルは、タイトルに「メモ」とあるように、何か結論を出すためのものという位置づけではない。
普段のようにある区切りまで書いて完結でなく、基礎を押さえつつ興味ある性質を追記していきたい。
とはいえ、延々と書くのもどうかと思うので、自然変換くらいまで等、ある程度のところで一度、閉めようと思う。
圏論とは何?
ある数学的構造が、当初、何を目的に導入されたかを知ることは大事であるため、簡単に記載する。
- Eilenberg , MacLane の論文がはじまりとされる。
- 出自は代数的位相幾何学(ホモロジーなど)と関係が深い。
- Haskellなど、関数型プログラミング言語に応用されている。
- 集合やそれに構造が入った数学的対象、それらの間の対応関係には、似通った構造が異なる対象において現れることがある。そういった大局的な構造について論じるものである。
- 特に「自然な」対応関係とは何か?というところがこの理論の出発点であったようだ。
- したがって、群論などの個々の分野を勉強する時より、かなり広い数学的対象について、より抽象的に扱う。
基本的概念
圏論で扱う基本的概念をここで確認する。前提となる定義や知識も適宜、記載していく。自分の復習という意味で基本的なものも書くので冗長なら適宜読み飛ばしてほしい。
- 基本的すぎる部分は、別記事 でまとめた
圏を構成するやり方は複数ありそうだったが、私は一番イメージしやすい集合の圏をベースに対象と射を考えてみる。
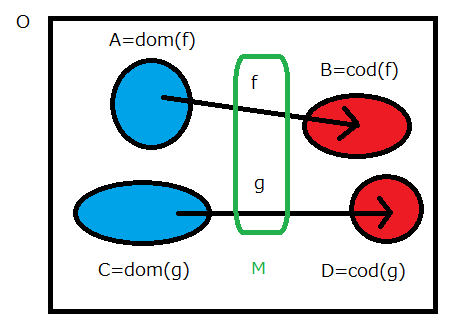
定義 (有向グラフ)
$G =(O , M , d , c)$ が有向グラフであるとは以下を満たすこと。
(1) $O$ は集合。$O$ の元について、 $v \in O$ を点(vertex)と呼ぶ
(2) $M$ は写像 $f : O \rightarrow O$ の集合。$M$ の元 $f \in M$ を矢(arrow) と呼ぶ。
圏論ではしばしば矢印を使った絵がよく見られるのでイメージしやすいと思う。
(3) $d , c$ は写像であり $d : M \rightarrow O$ , $c : M \rightarrow O$ である。
$f \in M$ に対し、 $d(f)=dom(f) \in O$ を $f$ のドメイン(domain) 、
$c(f)=cod(f) \in O$ を $f$ のコドメイン(codomain)という。
$dom(f) = A , cod(f) = B$ であることを $f : A \rightarrow B$ と書く。
定義 (圏 , Category)
圏 $C$ とは、以下を満たすような有向グラフ $G = (O , M , dom , cod)$ , 写像 $\circ : M \times M \rightarrow M$ の組 $C = (O, M, dom, cod, \circ)$ である。
このとき圏 $C$ において、 $O$ を対象(Object)、 $M$ を射(Morphism)といい、$Ob(C), Mor(C)$ と書いて、対象と射の組で以下(合成射、結合律、恒等射)を満たすものを圏と定義することもある。
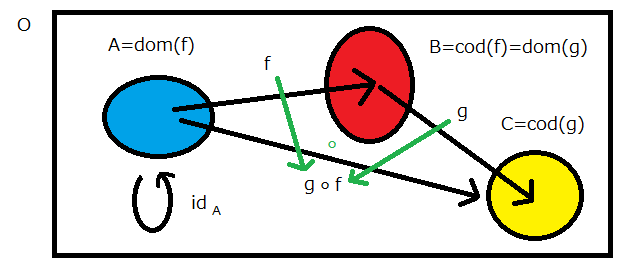
(1) 合成射
$f, g \in M$ に対して、$cod(f) = dom(g)$ を満たすとき、
$f$ と $g$ の合成射 $g \circ f$が定められ、
$dom(g \circ f) = dom(f) , cod(g \circ f) = cod(g)$を満たす
(2) 結合律
射の合成について、結合律を満たす。すなわち、
$f : A \rightarrow B , g : B \rightarrow C , h : C \rightarrow D$に対して
$h \circ (g \circ f) = (h \circ g) \circ f$ が成り立つ。
(3) 恒等射
$\forall A \in O$ に対し恒等射 $id_A : A \rightarrow A$ が存在し、射の合成について単位元となる。
即ち $\forall f : A \rightarrow B$ に対して $f \circ id_A = f$ かつ $id_B \circ f = f$
「対象」の定義について
圏の定義はあいまいに感じるものが多い。個人的にはずっと対象(Object)の定義の「あいまいさ」が引っ掛かっていた。議論する対象の範囲と大きさが広大であるし、導入として「敢えて」そうしているのかと思ったが、どうも多くの記事ではそうではなく、厳密な定義をしていないようだ。実はここまで自分で書いたものについても同様に感じており、やはり何か釈然としないものがある。厳密性だけでなく、対象が大きすぎたりしないか?というところも疑問なのだ。
ということで、ジュンク堂なんかで圏論の記載がありそうな本もいろいろ調べていたのだが、この件についてちゃんと書いてあったのは、「圏論の技法 アーベル圏と三角圏でのホモロジー代数」(中岡 宏行 著、日本評論社)であった。
圏論は扱っている数学的対象が非常に大きい。そのため、論理的に破綻しないよう工夫が要る、という話がやはり関連している。対象や圏を集合論的に問題が出ないよう定義するために、Universe (宇宙とか普遍集合と呼ばれる。特にグロタンディーク宇宙を用いる)というものを仮定し、その元を対象として議論することが多いようだ。
ただし 集合論メモ で触れたように、グロタンディーク宇宙はZFCから導くことができるわけではなく、公理という扱いとなる。命題全部をZFCからのみ導いているわけでなく飛び道具を追加で認めているという意味で、これを仮定しての圏論は厳密ではないという言い方をする方もいるようだ。
universe、宇宙というだけあって非常に大きな話をしているのだが、ぴんと来ない人は「すべての集合の集合」などを想像してみると、話の規模の大きさが想像できるだろうか?
この話は数学のかなり深いところにかかわっており、圏論というより数学基礎論のところの話(ZFCなど)に興味が移ってしまい、圏論としての議論が進まなくなりそうなので、ここではUniverseが存在するという仮定のもと、議論を進めることにする。
上記では、対象 $O$ として集合、射 $M$ として写像を想定しているような定義になっているが、後でこのUniverseを使って言い換えてみよう。
定義 (圏(その2) , category)
定義 (小さな圏、大きな圏)
圏 $C$ の対象 $Ob(C)$ が小さな集合である圏を小さな圏といい、対象がクラスである圏を大きな圏という。
記法 (射全体のなすクラス)
$dom(f) = X , cod(f) = Y$ である射 $f \in Mor(C)$ 全体のなすクラスを $Hom(X,Y) , Hom_{C}(X,Y)$ などと表す
具体例 (圏)
(1) 圏 $C$ = 集合の圏 $Sets$
対象 $Ob(Sets)$ の元は集合 $X, Y \in Ob(C)$ ,
射 $f : X \rightarrow Y \in Hom_{C}(X,Y)$ は集合の写像。
合成射は写像の合成で、これは結合律を満たす。恒等射は恒等写像。
(2) 圏 $C$ = 群の圏 $Grp$
集合に構造をいれたもの、たとえば群や位相空間を $O$ とし、
群準同型や連続写像を $M$ にして圏を構成することができる。
対象 $Ob(Grp)$ の元は群 $(G,\cdot) \in Ob(Grp)$ ,
射 $\varphi : (G,\cdot) \rightarrow (G',\cdot ') \in Hom_{C}(G, G')$ は群準同型。
合成射は群準同型の合成、これは結合律を満たす。恒等射は恒等写像。
(3) 圏 $C$ = 位相空間の圏 $Top$
対象 $Ob(Top)$ の元は位相空間 $(X,O(X)), (Y,O(Y)) \in Ob(Top)$ ,
射 $f : X \rightarrow Y \in Hom_{C}(X,Y)$ は連続写像
合成射は連続写像の合成、これは結合律を満たす。恒等射は恒等写像。
(4) 上記のほか、双対圏や関手圏などがある。これらはもう少し学習を進めてから理解する。
定義 (射の可逆、逆射)
対象 $X, Y$ , 射 $f : X \rightarrow Y$ に対し、 $f$ が可逆であるとは、ある射 $g : Y \rightarrow X$ が存在し、
\exists g : Y \rightarrow X \quad s.t. \quad \left\{
\begin{array}{ll}
g \circ f = 1_{X} \\
f \circ g = 1_{Y}
\end{array}
\right.
この $g$ を $f$ の逆射といい、 $g = f^{-1}$ と書く。可逆な射 $f$ を同型射という。
また、射 $f : X \rightarrow Y$ が同型射のとき、対象 $X, Y$ は同型といい、$X \simeq Y$ と表す。
```math
\exists g : Y \rightarrow X \quad s.t. \quad \left\{
\begin{array}{ll}
g \circ f = 1_{X} \\
f \circ g = 1_{Y}
\end{array}
\right.
`` `
$X \simeq Y$
命題 (逆射の一意性)
逆射は存在すれば一意に定まる。
(proof)
射 $f : X \rightarrow Y$ の逆射が2つあると仮定する。これらを $g , h : Y \rightarrow X$ とする。
このとき、 $g \circ f = 1_{X}$ , $f \circ g = 1_{Y}$ , $h \circ f = 1_{X}$ , $f \circ h = 1_{Y}$ である。
射は合成できるため、
$( g \circ f) \circ h = 1_{X} \circ h = h$ であり、 $(g \circ f) \circ h = g \circ (f \circ h) = g \circ 1_{Y} = g$ なので、$h = g$
または、
$( h \circ f) \circ g = 1_{X} \circ g = g$ であることから、 $(h \circ f) \circ g = h \circ (f \circ g) = h \circ 1_{Y} = h$ なので $g = h$ ともできる。
$\therefore fの逆射は、存在すれば1つに定まる(複数あると仮定しても結局、同じものが得られる)。\blacksquare$
定義 (亜群, groupoid)
任意の射が可逆である圏 $C$ を亜群という。
群に対しモノイドは逆元の存在を仮定しないが、同様に、亜群に対し圏は逆射の存在を仮定しない。
モノイドと群は演算に対して閉じているが、(圏の文脈での演算として射に注目すると)圏と亜群は射に対して閉じていない(対象が1つであるとは限らない = 射で写された先が同じ集合やクラスとは限らない)。
\begin{CD}
圏C @>{演算/射が閉じている}>{対象が1つともいう}> モノイドG \\
@V{可逆}VV @V{可逆}VV \\
亜群C @>{演算/射が閉じている}>> 群G
\end{CD}
定義 (エピ射 , Epimorphism , Epic morphism)
射 $f : X \rightarrow Y$ がエピ射または全射であるとは $f$ が右簡約可能であること。
すなわち、射 $\forall g_1, g_2 : Y \rightarrow Z$ に対し $g_1 \circ f = g_2 \circ f \: \Rightarrow \: g_1 = g_2$ が成り立つこと。
定義 (モノ射 , Monomorphism , Monic Morphism)
射 $f : X \rightarrow Y$ がモニック射あるいはモノ射、単射 (monomorphism, monic morphism) であるとは $f$ が左簡約可能であること。
つまり射 $\forall g_1, g_2 : Z \rightarrow X$ に対し $f \circ g_1 = f \circ g_2 \: \Rightarrow \: g_1 = g_2$が成り立つこと。
定義 (関手 , Functor)
$C, D$を圏とする。このとき、関数 $F : C \rightarrow D$ で $A \in Ob(C)$ に $F(A) \in Ob(D)$ を、 $f \in Mor(C)$ に $F(f) \in Mor(D)$ を対応させ以下を満たすものを関手という。
(1) $A , B \in Ob(C)$とし、$f : A \rightarrow B$のとき$F(f) : F(A) \rightarrow F(B)$
(2) $f , g \in Mor(C)$とし$cod(f) = dom(g)$ のとき$F(g \circ f) = F(g) \circ F(f)$
(3) $A \in Ob(C)$に対して$F(id_A) = id_F(A)$
定義 (恒等関手)
定義 (双対圏、逆圏)
定義 (共変関手 , covariant functor)
$C, D$を圏とし、$F : C \rightarrow D$を関手とする。
$F$ が共変関手であるとは、以下を満たすこと。
(1) 関手 $F$ は, 圏 $C$ の各対象 $X \in Ob(C)$ を圏 $D$ の各対象 $F(X) \in Ob(D)$ に対応させる
$\forall X \in Ob(C) \: , \: \exists Y \in Ob(D) \: s.t. \: Y=F(X)$
(2) 関手 $F$ は、恒等射および射の合成を保存する。つまり以下を満たす
(2-1) 関手 $F$ は、圏 $C$ における射 $f : X \rightarrow Y$ を
圏 $D$ における射 $F(f) : F(X) \rightarrow F(Y)$ に対応させる
(2-2) $\forall X \in Ob(C) \: , \: F(id_X) = id_{F(X)}$
(2-3) $\forall f : X \rightarrow Y, \forall g : Y \rightarrow Z \: , \: F(g \circ f) = F(g) \circ F(f)$
定義 (反変関手 , contravariant functor)
$C, D$を圏とし、$F : C \rightarrow D$を関手とする。
$F$ が反変関手であるとは、以下を満たすこと。
(1) 関手 $F$ は, 圏 $C$ の各対象 $X \in Ob(C)$ を圏 $D$ の各対象 $F(X) \in Ob(D)$ に対応させる
$\forall X \in Ob(C) \: , \: \exists Y \in Ob(D) \: s.t. \: Y=F(X)$
(2) 関手 $F$ は、恒等射を保存するが、射の合成は反転させる対応となる。つまり以下を満たす
(2-1) 関手 $F$ は、圏 $C$ における射 $f : X \rightarrow Y \quad (X, Y \in Ob(C))$ を
圏 $D$ における射 $F(f) : F(Y) \rightarrow F(X) \quad (F(X), F(Y) \in Ob(D))$ に対応させる
(2-2) $\forall X \in Ob(C) \: , \: F(id_X) = id_{F(X)}$
(2-3) $\forall f : X \rightarrow Y, \forall g : Y \rightarrow Z \: , \: F(g \circ f) = F(f) \circ F(g)$
定義 (自己関手)
定義 (圏同値)
定義 (圏双対)
定義 (自然変換)
定義 (随伴関手)
定義 (モナド)
定義 (デカルト閉圏)
定義 (カリー化)
参考
以上