異常検知入門3 変化点検知

Aidemy　2020/11/10

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、異常検知の3つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・累積和法を使った変化検知
・近傍法による異常部位検知
・特異スペクトル変換法

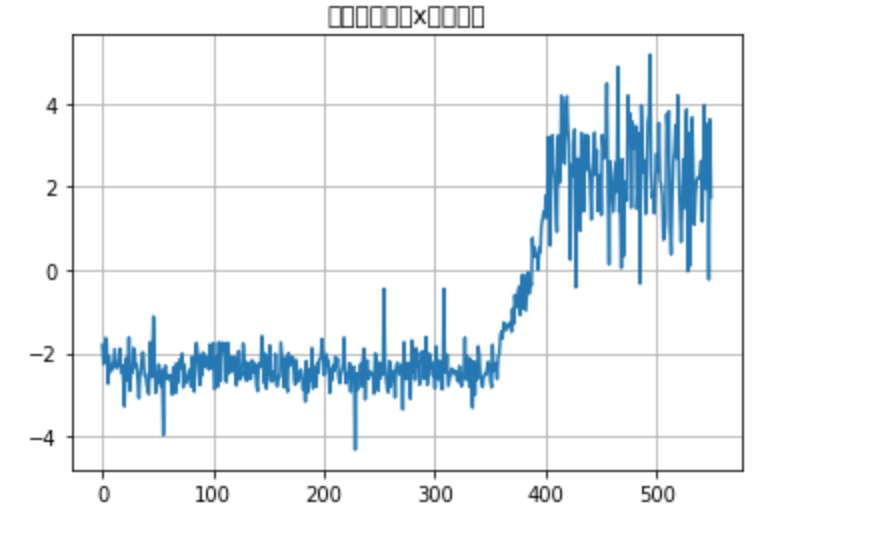
累積和法による変化検知

累積和法とは

・累積和法は変化点（Chapter1参照）を検出する「変化検知」の一手法である。変化検知は外れ値の検出と違って「継続的な異常」が発生するので、これを検出できる累積和法が使われる。
・累積和法は「異常である状態（変化度）」を時間に沿ってカウントし、そのカウント（累積和）が閾値を超えたときに異常と判定する。つまり、時系列データにおける何らかの値の異常を検知するときにはこの手法が適していると言える。

・累積和法（変化が上振れ、つまり上昇するのが異常である場合）の流れは以下の通りである。
　①正常時の目安と上振れの目安を与えて変化度を定義する
　②変化度の上側累積和を求める
　③閾値を超えていたら異常と判断する

①正常時の目安と上振れの目安を与えて変化度を定義する

・変化度とは、データがどれぐらい異常状態に変化しているかを示す値である。
・ここでは変化度を定義するが、それには、「正常であるときに取る値（μ）」「異常と判定する上振れの値（ν+）」を事前に（過去の事例を分析して）取得する必要がある。
・また、データから「標準偏差（σ）」も求めておく。「np.std()」で求められる。
・ここまで求めたら、時刻tにおける変化度（a+(t)）は以下のように求められる。
$$
a_{+}(t) = \left( \frac{\nu {+}}{\sigma} \right)\frac{{ x(t)} - \mu - \nu _{+} / 2}{\sigma}
$$
（式の「x(t)」_は、時刻tにおける観測値）

・これにより、データが正常な時は変化度が負になり、異常な時は正になるので、累積和で処理することが可能になる。
・また、今回は変化が上振れの時を考えたが、下振れの時も同じように計算できる。

・コード（正常時10、上振れ時14として変化度を計算）

・結果

②変化度の上側累積和を求める

・前項で変化度を求めたので、次はそれを累積していく。前項で定義した変化度では、正常な時は負の値をとるが、累積するにあたっては、正常時は0となるようにする。つまり、異常な時だけ変化度は上昇していく。これが、上側累積和である。
・上側累積和の算出は、forループを使って変化度を一つ一つ取り出して足し合わせることによって行う。具体的には以下の通り。

・上記コードの解説
・for文の「range(x.size - 1)」の部分で「-1」しているのは、時刻tまでの上側累積和は「t-1までの変化度の合計 + tの変化度」で求められるため、この「t-1」を表現するためにこのように取り出している。
・「max(0, x_cumsum[i])」は、累積和を格納する配列には「0と変化度の大きい方を格納する」ことを示す。
・「x_cumsum[i + 1] = x_cumsum[i] + x[i + 1]」の「i+1」は、iがt-1を表しているので、実質的に「t」であることを示す。

・上側累積和をグラフにすると以下のようになる。

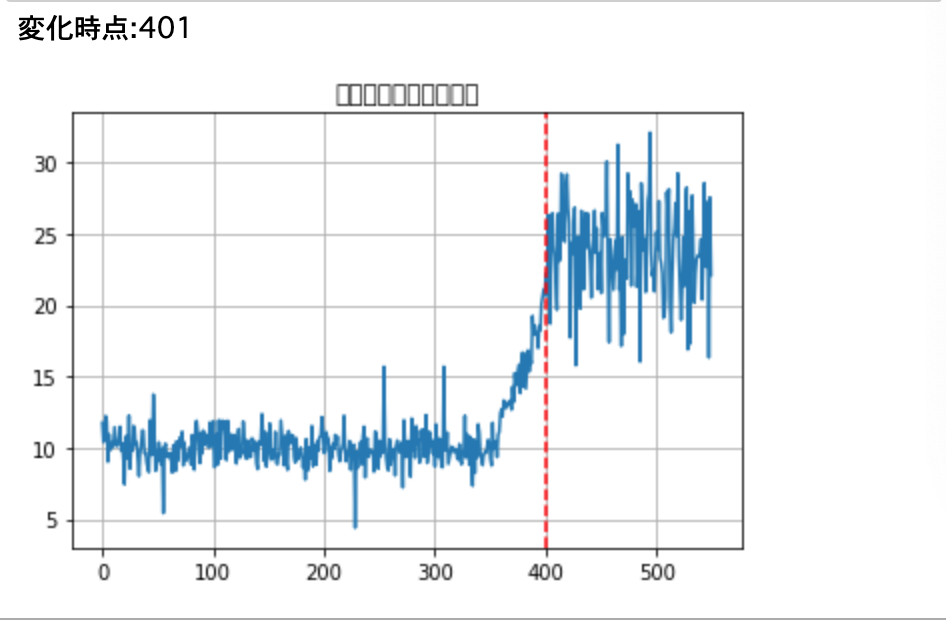
③閾値を超えていたら異常と判断する

・あとは、今までの手法と同様に、閾値と累積和を比較して異常かどうかを判定すれば良い。
・また、初めて閾値を超えた点、すなわち「変化点」を見つけるには、「0から累積和の大きさまでの間で、初めてpred==1となったインデックス」を求めれば良いので、以下のように記述できる。

np.arange(score_cumsum.size)[pred==1][0]

・「np.arangeで範囲を0~累積和の大きさに限定して一つずつ参照し、[pred==1]で初めて異常と判定された部分を抽出し、[0]でインデックスを取り出す」ということが行われている。

・異常について行ったものが以下になる。

・結果

近傍法による異常部位検出

スライド窓、部分時系列

・今回は、時系列データを「外れ値検知」で異常検知を行う。前項までの累積和法では閾値や変化点計算のパラメータなどを自分で用意しなければならず、あまり実用的ではないというデメリットがあったが、近傍法を使うことで、この問題を解消できる。
・外れ値検知は時系列データの変化検出に向いていないのであるが、それは、時系列データのような継続的なデータを観測できないからである。今回の近傍法では、そのような問題を解決するように工夫することで、これを可能にしている。
・具体的には、各データをM個の隣接したデータとしてまとめる、すなわち、M次元のベクトルの集まりに変換することで、時間的な影響を考慮することを可能にする。
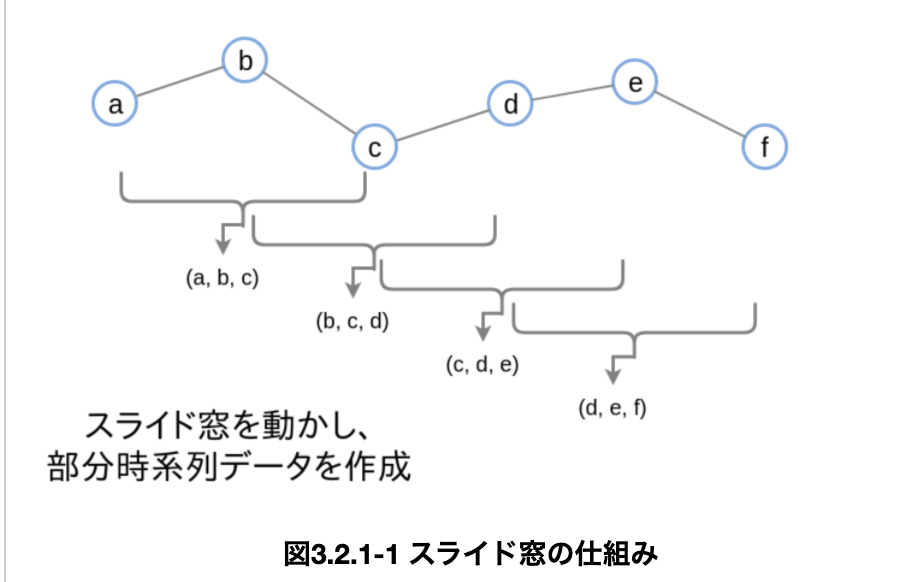
・この時の「M」個に分ける長さを「スライド窓」といい、これによって作成されたベクトルの集まりを「部分時系列データ」という。例えば、以下では長さ3のスライド窓を使ってデータを変換している。

・コードとしては以下のようになる。データを一次元から二次元に変換したあと、スライド窓Mの個数分のデータを分割し、それを抽出することで作成する。

・コード（550個のデータxを部分時系列データに変換）

・以上を実行した時、部分時系列のデータの長さは「((データ数 - M + 1), M)」となる。

異常度の計算

・部分時系列データを作成したら、異常度を計算していく。今回は、最近傍との距離を異常度とした「最近傍法」を使っていく。詳しくはChapter2参照。KNeiborsClassifierを使って最近傍との距離を算出していく。
・今回の「n_neighbors」は、1ではなく2に設定する。データの最近傍は「そのデータ自身」と扱われてしまうためである。そのため、最近傍距離は「2番目に近いデータの距離」ということになる。
・よって、「clf.kneighbors()」で各データの近傍距離を算出し、そこから「dist[:, 1]」で二番目に近いデータの距離を取得すれば良い。

・コード

閾値の設定、異常判定

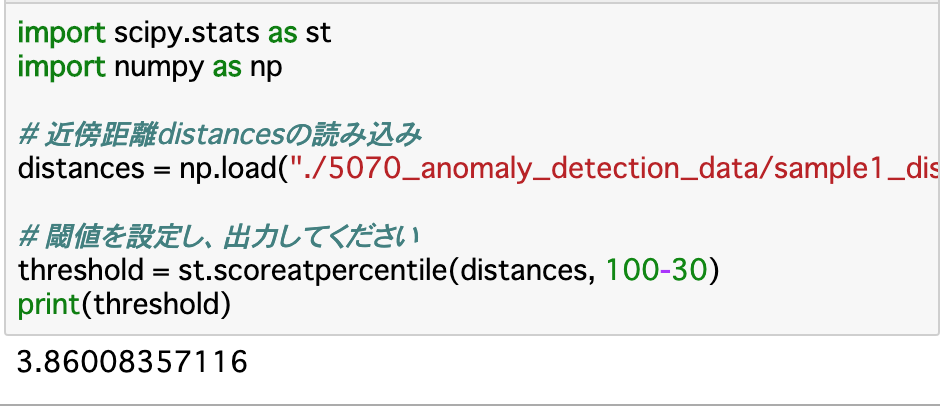
・次に、閾値を設定する。この手法ではデータの分布を定義しないので、1クラスSVMと同じように閾値を設定する。
・具体的には「st.scoreatpercentile()」を使用する。「データには一定の割合で異常データがある」と仮定して、その割合「a」を設定し、異常度「distances」を渡すことで閾値を設定してくれる。
・今回は異常度が大きいほど異常であるというようにしたいので、引数に渡す分位点は「100-a」とする。

・コード（上位30％を分位点とする場合）

特異スペクトル変換法

履歴行列とテスト行列

・前項までの部分時系列データによって、過去と現在を分けることで、より高度な分布を考察することが可能になった。今回学ぶ「特異スペクトル変換法」は、この高度な分布を定義することで「現時点のデータを代表するベクトルと過去のデータを代表するデータ」の二つを求め、この二つの差異を変化点とすることで異常検知を行うという手法である。
・特異スペクトル変換法の流れは以下になる。
　①時系列データに対し、窓幅M、履歴行列の行数n、テスト行列の列数k、ラグLを与える
　②データを窓幅Mの部分時系列データに変換する
　③履歴行列とテスト行列を作る
　④履歴行列とテスト行列を特異値分解し、それぞれの左特異ベクトルの行列を求める
　⑤2つの行列の差異から変化度を計算する

・以上で出てきた「履歴行列」とは、「現時点から時間的に一つ前のデータをn個集めて並べたもの」である。また「テスト行列」は「現時点からL（ラグ）進み、そこからk個前までのデータを並べたもの」である。視覚的には以下を参照。

・①について、今回は「M=50,n=25,k=25,L=13」を使用する。
・②について、部分時系列データへの変換は「近傍法による異常部位検出」で行った手法と同様に行う。
・③について、②で作成した部分時系列データ（X_pts）から履歴行列とテスト行列の作成方法は以下を参照。

④履歴行列とテスト行列を特異値分解し、それぞれの左特異ベクトルの行列を求める

・③で作成した履歴行列とテスト行列に対して、「特異値分解の低階層近似」というものを行うことで、行列を代表する値を求めることができる。
・コードとしては、（m×n）の行列Aを特異値分解する時は「np.linalg.svd(A)」で行う。格納する変数としては、「U,S,V」の3つを用意する。今回使用するのは、そのうちの「U」である。Uには左特異ベクトルというものが格納されている。左特異ベクトルとは、行列Aの代表的なベクトルのことであり、Uはこれが優先度の高い順に並べられた行列になっているので、以下のように階層「r」で指定することで、より優先度の高い代表ベクトルを取り出せる。
・また、Uのshapeは（行列の行数,窓数M,左特異ベクトルの個数）というようになっているので、低階層近似をするときは、第3軸をスライスする。

・これらを行ったコード([0]の部分は「U」のみを取り出している)

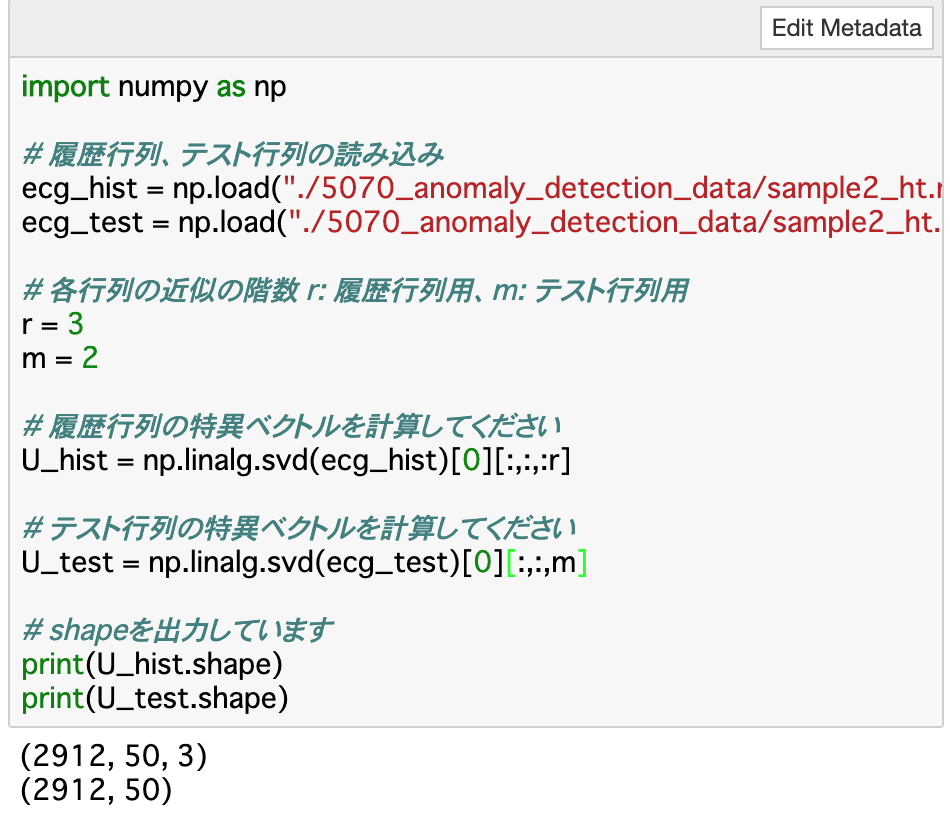
⑤2つの行列の差異から変化度を計算する

・前項で作成した二つの左特異ベクトルの差異を求めていく。差異はベクトルの内積で求められる。今回はベクトルの集合、すなわち行列同士の内積を「np.matmul()」で計算し、さらに「np.linalg.norm()」で距離を求める。
・この距離をnormとすると、変化度は「1-norm」で求められる。

・これらを行ったコードは以下のようになる。

・結果

・以上のコードについて補足
・「get_score」は変化度を求める関数を自分で作成する。np.matmul()では「x.T」のように、履歴行列の方を転置させる必要がある。
・「score」の方は、上記get_scoreにU_histとU_testをまとめて渡している。for表記になっているのは、各時間における変化度を計算しているからである。

まとめ

・時系列を持つ変化点検知の一手法として、「累積和法」がある。これは変化度を累積（足し算）していき、閾値以上になったら異常と判定する手法である。ただし、この閾値や計算のパラメータは自分で算出しなければならず、実用的ではない。
・この問題を解消するのが「近傍法」を使った手法である。この手法は時系列データを外れ値検知で異常かどうかを判定するものである。本来外れ値検知と時系列データは不和であるが、隣接したデータをM個ずつに分けることでこれを解消している。
・この時のM個に分ける長さをスライド窓、作成されたデータの集まりを部分時系列データという。これらを使って異常度を最近傍法によって算出する。
・以上の手法を応用した「特異スペクトル変換法」というものも存在する。これは「現時点の代表データとかこの代表データの差異」から変化点を検出する手法である。

今回は以上です。最後まで読んでいただき、ありがとうございました。