Aidemy 2020/11/16
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、強化学習の3つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・動的計画法について
・TD手法について
動的計画法
動的計画法とは
・Chapter2では__ベルマン方程式__を使って最適な方策を見つけるということを説明したが、このChapterでは__実際にこれを行っていく__。
・環境のモデルが__「マルコフ決定過程(MDP)」で完全に与えられているとするとき、最適な方策を求める手法を「動的計画法(DP)」__という。
方策評価
・手法$\pi$をとった時の価値関数$V^\pi(s)$を計算することを__方策評価__という。実行方法は以下の通り。
・まず方策を更新する際の閾値$\epsilon$を事前に設定する。そして方策$\pi$を入力し、$V(s)$を全ての状態において__0__と仮定し、更新時に全ての状態の差分が__閾値よりも小さくする__ために、「$\delta$」を定義しておく。
・ここまで定義したら、全ての状態sについて、「v=$V(s)$」として、ベルマン方程式で「$V(s)$」を計算する。更新量を比較するために、あらかじめ定義しておいた「$\delta$」を「$\max(\delta,|v-V(s)|)$」に更新し、これが「$\epsilon$」を__下回ったら__その時点で計算を終了し、「$V(s)$」を「$V^\pi(s)$」の近似解と仮定して出力する。
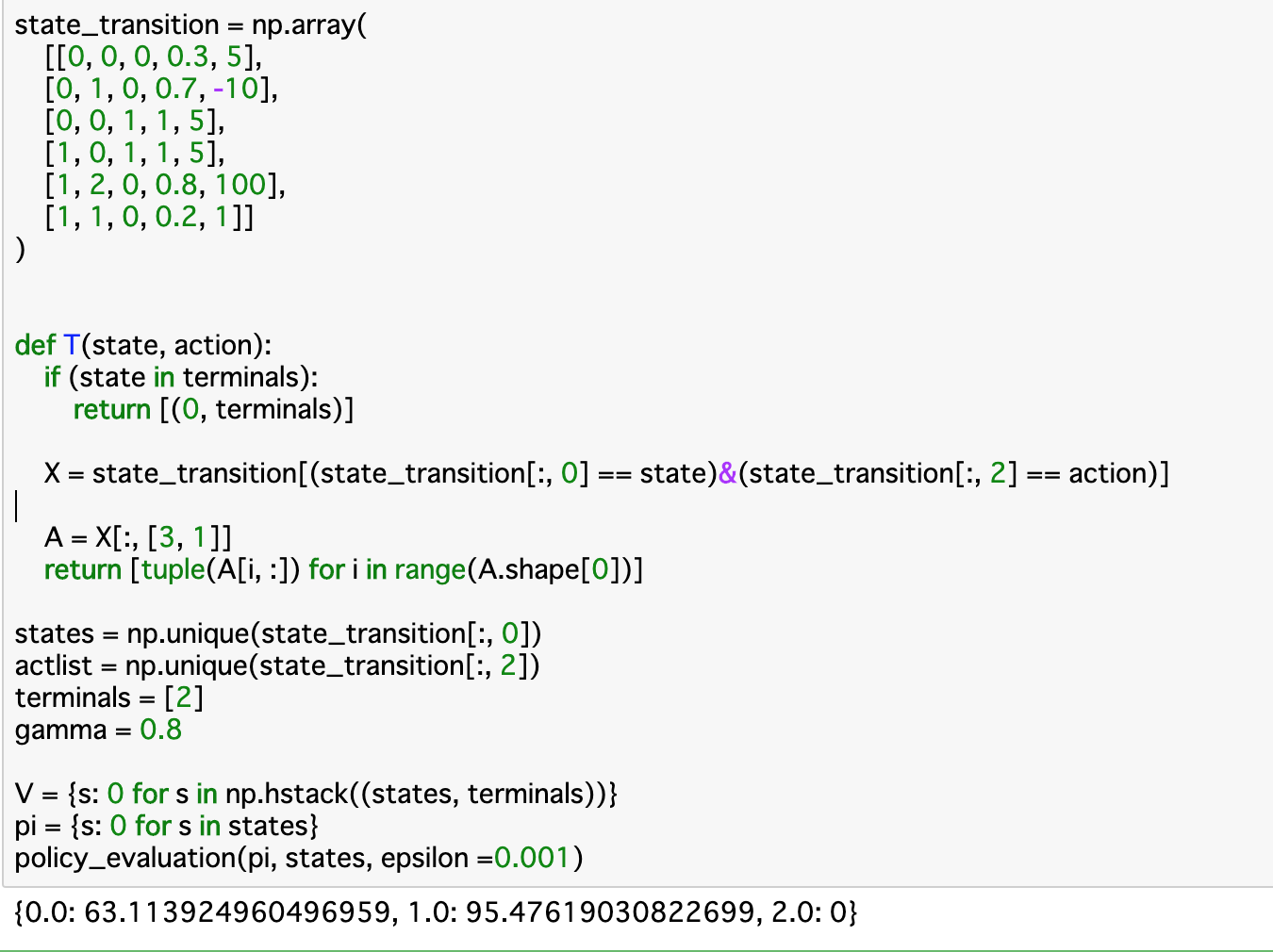
・以上についてのコードが以下である。
・方策評価を行う関数__「policy_evaluation()」について、引数には「方策pi、状態states、閾値epsilon」を渡す。
・はじめに「$\delta=0$」を定義する。そして、ここからは__全ての状態sについて__上記手法を行なっていく。まずは「v=V.copy()」で変数「v」に価値関数Vを代入する。また、次の計算で算出される「V[s]」を格納する変数「x」も用意しておく。
・「for (p, s1) in T(s, pi[s]):」について、「p」はエピソードTで得られる「そのActionを起こす確率($\pi(a|s)$)」で、「s1」は「遷移先のState(after_state)」である。これらを使って__ベルマン方程式(Chapter2の公式参照)で$V(s)$を計算する。これを__「x」__に代入する。
・この$V(s)$と$v(s)$を使った上記の式で「$\delta$」を計算し、閾値「$\epsilon$」を下回ったら価値関数の近似値「V」を返す。
・実行部分を見てみると、__「policy_evaluation()」__の「v」部分に当たるVと、引数で渡すpiを定義している。関数を適用した結果、__StateAの価値関数__と__StateBの価値関数__がそれぞれ算出されている。
方策反復
・前項の価値評価によって算出された「$V^\pi(s)$」において、greedy手法__をとるような方策を「$\pi'$」とすると、「$V^\pi(s)$ < $V^{\pi'}(s)$」__となることが知られており、これを__価値改善__という。
・この__価値改善と価値評価を繰り返す__ことで、最適価値関数を導出__することができる。このことを__方策反復__という。
・価値改善を行う関数「policy_iteration()」__のコードは以下のようになる。
・上記コードについて、まずは__価値関数Vと方策piを初期化__する。これを行なったら、Vについて、Chapter2で作成した関数「policy_evaluation()」で__方策評価を行う__。同時に、__「policy_flag=True」とする。
・各状態sについて、更新したVを使ってゲルマン方程式で方策piを算出し、これに従って__actionをソートする。そして、__方策が被ってなければ__piにactionを格納してループを継続する。これが終了したら方策piを返す。
・方策反復関数__「policy_iteration()」__は方策piを返すので、この実行結果は「StateAの時ActionXを取り、StateBの時ActionXをとる」という方策を表している。
価値反復
・前項の方策反復は、方策piを計算するために__毎回全ての状態について価値関数を計算し直すことを__複数回__おこなわなければならず、状態が増えるほど計算量も多くなってしまう。これを解決するのが「価値反復」__という手法である。
・価値反復では、価値vを計算するために__各状態sについて、価値関数を直接求めて更新する手法を取るので、価値関数の計算は一度で済む。
・以下は価値反復関数「value_iteration()」__のコードである。
・この関数について、まずは__状態価値Vを今までと同様に初期化する__。方策反復と違って__方策piは考慮されない__ので、piの初期化を行う必要はない。次に、各行動について、方策評価__を行って計算される$V(s)$の__最大値を更新__する。
・最後に、この$V(s)$から最も報酬が得られる行動を計算__し、方策「pi」として返す。この時の最も報酬が得られる行動は前項の方策反復の時と同じように計算できる。
TD手法
TD手法とは
・以上の手法は__動的計画法__であり、状態遷移確率Pがあらかじめわかっていければならない_。逆に、状態遷移確率がわかっていない時はChapter1で学んだように、実際に集めた報酬からこれを推定していく__必要がある。
・この推定方法として「TD手法」というものがある。TimeDifferanceの略で、最終結果を見ずに__現在の推定値を利用__して次の推定値を更新するという方法で行われる。
・TD法には、「Sarsa」「Q-learning」__といった手法がある。
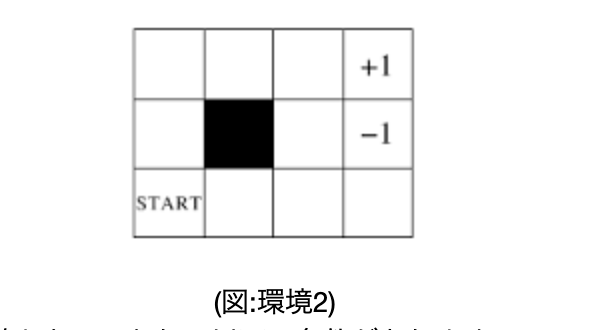
・開始地点は図の「start」のマス、終点は「+1」または「-1」のマス、黒いマスは遷移不可で、隣のマスの上下左右に動くことができる。また、8割__の確率で、選択した通りに遷移することができるが、1割__で選択した向きの90度時計回りに遷移し、残り__1割__で反時計回りに遷移する。報酬は、終点のマスは__その点数、それ以外のマスは「-0.04」であるとする。
・以下のコードは、スタート地点から「上に二つ、右に三つ」__進もうとした時の位置を出力する関数である。
・新しい環境を使うので、まずはそれを定義する。エピソードを定義する関数__「T()」は、「take_single_action()」で使用するため、0列目が__probabilily,1列目が__next_state__の配列を返すように定義する。また、next_stateの状態を変化させるため、stateとdirectionから__移動先__を定義する__「go()」も作成する。
・遷移確率に基づいて__次の状態を決定する関数__である「take_single_action()」はここでも使用する。上記「T()」で定義した「遷移確率」がxを越えるまで「次の状態」を更新し、更新が終了した時点での報酬を設定する。
・最後に、実際に「今いるstateから上に2回右に3回」移動する関数「move()」__を作成する。actionsとして、__0列目が上下の動き、1列目が左右の動き__を定義し、0列目について2回take_single_actionで移動し、同様に1列目について3回移動してstateを更新する。
・環境についてはそれぞれのマスを定義している。初期地と終点も定義し、move()を使うことで移動後のstateがわかる。
Sarsa
・Sarsa__はTD手法の一つで、ベルマン方程式__を試行錯誤しながら解いていくものである。価値反復などでは$V(s)$を使っていたが、ここでは__行動価値関数$Q(s,a)$を使用する。このQ関数は[全ての状態×全ての行動]__の配列で表す。
・この時の「全ての状態」について、環境2では、取りうる状態は11通り、「全ての行動」は上下左右の4通りである。よってQ関数は11×4の配列にしたいのだが、状態は座標で表される__ため、これをうまく表現できない。よって、状態の部分は「x座標×10 + y座標×1」__で対応させる。
・__「get_action()」__は、後で定義する__Q関数(q_table)の最大値によって行動を決定する関数である。この時渡される「t_state」は、先述した「座標を変換したstate」である。
・「take_single_action()」は今までのものと用途は同じだが、返される値として、rewardが設定されていない場合、すなわち__行動先が壁や障害物で移動できない時__は、その場に止まると言う意味で、状態「state」とreward「-0.04」を返し、rewardが設定されているマスにいるときは「next_state」とそのrewardを返す。
・「update_qtable()」__は実際に__行動価値関数Qを算出__し、更新する関数である。この更新の時に使われる公式は以下である。
$$Q(s,a) += \alpha[r + \gamma Q(s',a') - Q(s,a)]$$
・この$\alpha$は__学習率__であり、事前に設定しておく必要がある。今回は__「0.4」で設定する。また、割引率$\gamma$は「0.8」とする。また、この時渡される状態も、「座標を変換したstate」とする。計算自体は公式通りに行えば良い。
・最後に、状態「state」を「座標を変換したstate」にする「trans_state()」__関数を作成する。
・Sarsaを実行するにあたり、まずは__行動価値関数Qを初期化__する。今回はエピソード数は500、時間ステップは最大1000回とし、またエピソードの終了条件として__「5回連続で平均報酬が0.7以上」を設定するため、これを管理する配列も準備する。環境などは前項と同じ。
・次に、500回の各エピソードについて、(終了条件を満たすまで)以降の全てを繰り返す。
・まずは__stateを初期化__する。これに基づいて、Q関数に渡す「t_state」、行動「action」を計算する。それぞれ「trans_state()」「get_action()」関数を使用する。
・次に、エピソード中の各時間ステップについて「take_single_action()」__で、行動aを行なった場合の次の状態s'と報酬rを取得し、報酬を累積__していく。また、状態s'についてもQ関数に渡す「t_next_state」、行動「next_action」を計算する。
・これらを「update_qtable()」__に渡して、行動価値関数を更新__する。また、次の時間ステップに行くためにstateやactionも更新する。
・最終的に終点についたら、そのエピソードは終了し、次のエピソードに移動する。移動する前に、エピソード終了条件である報酬について「total_reward_vec」を更新__し、それを出力する。同様に、終了したエピソードの番号と、それが何ステップで終了したかを出力する。
・もしこの「total_reward_vec」の__最小値__が0.7を超えたらエピソードの繰り返しも終了する。
・実行結果をみてみると、報酬が「0.2」であったエピソードが直近5エピソードから除外され、全ての報酬が0.7を超えたエピソード21+1で終了している。
Sarsaでのε-greedy手法の実装
・前項の手法では、Q関数の最大値のみを選択していたが、これでは__より優れた手法を見逃す恐れ__がある。これを避けるために、ε-greedy手法__を使って新しい手法を探索していく。
・Chapter1でもε-greedy手法を使ったが、少し変えて使用する。今回は、「episodeが早いうちはεを大きくして探索の割合を増やし、episodeが進むにつれてεの値を小さくして探索を狭めていく」__というやり方を使う。式としては以下のものを使う。
$$\epsilon = 0.5 * (1 / ( episode + 1)) $$
・具体的なコードは以下の通りで、「get_action()」部分だけが異なる。
・上記関数について、まずは「epsilon」を上の式で算出。このepsilonが一様乱数「np.random.uniform(0,1)」以下であれば、__前項と同様にQ関数の最大値に基づいて次の行動を決定__し、そうでなければ__ランダムに次の行動を決定する__こととしている。
・実行部分についてもほとんど前項と違いはないが、初めに定義している__「action」__は乱数が絡むget_action()を適用せず、Q関数の最大値を使って決定している。next_actionについてはこの関数を使用している。
Q学習
・Sarsaとは別のTD手法として__「Q学習」__と言うものがある。Sarsaと基本的には同じで、違う点について、各時間ステップの処理において、__次の行動を決定してからQ関数の更新を行う__のがSarsaであるのに対して、Q関数の更新を行ってから次の行動を決める__のがQ学習である。
・よって、関数「update_Qtable()」には「next_action」___は渡さず、その代わりにnext_stateにおける__Q関数の最大値「next_max_q」__を算出し、これを使ってQ関数を更新する。これ以外はSarsaと全く同じ。
まとめ
・環境のモデルがマルコフ決定過程で完全に与えられているとき、Chapter2のベルマン方程式を使って最適な方策を最適な方策を求める手法のことを「動的計画法(DP)」という。
・ある手法$\pi$をとったときの価値関数$V^\pi(s)$を計算することを方策評価という。また、greedy手法をとったときの方策の方が価値関数は大きくなることが知られており、これを価値改善という。評価と改善を繰り返すことで最適な手法を見つけることができ、これを方策反復という。
・方策反復の応用として、方策ではなく価値を計算するために価値関数を更新する手法のことを価値反復という。これにより、価値関数の計算量が大幅に減らせる。
・方策反復や価値反復は動的計画法で、状態遷移率が与えられたモデルにのみ使用できるため、これが与えられていないモデルに対しては、TD手法というものを使用する。TD手法にはSarsaやQ学習がある。
・SarsaやQ学習はベルマン方程式により、行動価値関数Qを算出することで最適な方策を考える。
今回は以上です。最後まで読んでいただき、ありがとうございました。