More than 3 years have passed since last update.

株式会社LIFULL

因果推論におけるCausal Impactの立ち位置を俯瞰する

Last updated at 2020-04-30Posted at 2020-04-12

#マーケティングの実務で使えるデータサイエンス
※I'm quite welcome to get your feedback or MASAKARI..

#序論

　オフライン広告の効果検証は難しい. 具体的には, TVCMやタクシー・電車などの交通広告は, オンライン広告で可能なタグやCookieによるユーザー特定・紐付けなどが難しいため, 施策の効果測定の難易度もかなり上がる.

　ただ, ここで思考停止して諦めてしまっていいだろうか? 幸いにも, 世界の統計学者(広く研究者)たちはこうした因果効果の推定のための理論や技術を長年にわたり発展させてきた.

　無論, 現実と1mmのズレもない完璧な効果の測定や因果の推論を常に達成できる訳ではない. しかし, ある施策の純粋な因果効果を観測する上で含まれるバイアス(誤差)をminimizeするための道具は, 既に我々の手元に幾つか存在している.

　今回は, 私が実務においてGoogle JapanオフィスのData Scientistの方々との協力を通して利用した, CausalImpact(Google Inc , 2015)という時点数が多い時系列データに応用できる「欠測データ解析」の解説とその予測精度向上の手段を実務レベルで解説する.

　その上で最初に, CausalImpact(以下CI)をより本質的に理解する上で必要となる統計的因果推論の前提知識を整理していく.

###対象読者

　統計的因果推論の初学者で, WEB/アプリ系の企業で働いている...

データアナリスト
データサイエンティスト

###統計理論

Rubinの因果推論モデル
欠測データ解析
状態空間モデル

###使用言語

#本論

###構成

統計学における誤差(バイアス)
実験レベルとバイアス調整の関係
潜在的アウトカム(反事実)と欠測データ解析
CausalImpactとcovariate(共変量)
状態空間モデルによる予測精度の向上

###前提: スコープについて

　CIの実装自体は, それほど難しくない. 実際, CIの元論文のpublisherの1人であるKay Brodersenは, こちらの動画で, 基本的に以下の "just 3 lines of code" で欠測データのモデリングが完結すると紹介している.

library("CausalImpact")
impact <- CausalImpact(data, pre.period, post.period)
plot(impact)

　ただ, 世の中にはCIをきっかけに, 統計的因果推論に出会う人間も少なからずいるだろう. そこで今回はCI(欠測データの予測モデル)の精度向上のTipsだけでなく, CIの因果推論の系譜における立ち位置を明らかにすることで, データ分析者にとってより解像度の高い理解を実現したい.

　また余談になるが, 最初に因果推論の前に"統計的"と付けたのには明確な理由がある. 詳しくは津川氏のブログを参照して頂きたいが, 因果推論には統計学出身の概念と疫学や計量経済学出身の概念がある. そのため, 漢字からして似たような意味を持つ言葉同士の違いが何なのかに困惑することが予想される.

　具体的には, 交絡因子(cofounder)と共変量(covariate)などがそれに当たる. これらは完全に同義ではないものの, 各学問の因果推論において同じ立ち位置や似た文脈で振る舞うことが多いため必要以上の混乱に気をつけたい.

　ではまず前提知識として重要となる, 統計的因果推論における「誤差(bias)の種類」と「実験レベル」という2つの概念を整理する.

##1. 統計学における誤差(バイアス)

　統計的因果推論(statistical causal inference)を理解する上で, 重要となるキーワードは「バイアス(bias)」である.

　因果推論のゴールがシンプルに2つあるとすれば, まずは「因果関係(causality)」の有無の検証であり, 次に「因果効果(causal effect)」のボリュームの推定であろう. そしてそのプロセスは基本的に, 観察された結果変数(観察データ)からバイアス(誤差の1種)を取り除く作業に集約されると言っても過言ではない.

　これを変数同士の関係性で表すと, 下記の式で考えられる. ※厳密には欠落変数: $U_{Omitted\hspace{1pt}variable}$などの変数も存在する

Z_{Causality} = Y_{Outcome} - X_{Bias}

　　
　ここではまず, 統計的因果推論における「誤差の種類」を再整理する, 以下に誤差の種類とその構造を表にまとめた.

誤差	バイアス	調整方法	when	how	what
系統誤差	交絡	実験デザイン	実験前	限定・無作為化・マッチング	傾向スコアマッチング
系統誤差	交絡	統計解析	実験後	層化・標準化・多変量解析	DID・CausalImpact
系統誤差	選択バイアス	実験デザイン	実験前	-	-
系統誤差	情報バイアス	実験デザイン	実験前	-	-
偶然誤差	-	-	-	-	-

　上にある表の通り, 統計学では誤差をまず, コントロール可能な「系統誤差(systematic error)」と完全にランダムな「偶然誤差(random error)」に分けて考える.

　その上で系統誤差は, "Bias"(Miguel Delgado-Rodrı´guez&Javier Llorca, 2004)によると大きく以下3つのバイアスに分類できる. それは「交絡(cofounding)」,「選択バイアス(selection bias)」,「情報バイアス(information bias)」である.

　今回は上記の3つのバイアスのうち, 「交絡(cofounding)」のみに焦点を当てる. その理由は, 統計的因果推論の技術を用いてバイアスを調整する(除外する)タイミングに起因する. 結論から言うと, "実験後"に調整できるバイアスは「交絡」のみとなる.

　より詳しく説明すると, 研究者にとってバイアス(系統誤差)を調整できるタイミングは, 「データ収集前」と「データ収集後」の2度存在する. また各タイミングにおける調整手法は, 前者は「実験デザイン」, 後者は「統計解析」が存在する.

　しかし, 最終的なバイアス調整結果の信頼度や欠測データ解析の作業負荷は, 次の話題である「実験デザイン」の段階における「実験レベル(experiment level)」の設計に大きく依存するためその重要性にも触れたい.

##2. 実験レベルとバイアス調整の関係

　ここでは, 「実験レベル」というあまり触れられることがない上流の話をする. しかしこれが, 因果推論においてバイアス(交絡)を調整する上で本来は重要となる. 詳しくはこちらを参照してほしい.

　まず, 研究デザインは大きく分けて「Level 1. 実験レベル(介入研究)」と「Level 2. 準実験レベル(観察研究)」に分類される. また, 前者の実験(experiment)から得られるデータを「実験データ」, 後者を「観察データ」と区別する.

　具体的には, A/Bテストなど系統誤差(バイアス)を制御するために行われるRCT(ランダムか比較試験)は実験レベルに当たり, 実験前のバイアス調整が甘く, なんらかの交絡を含んだ観察データに対する差分の差分析(DID)などは準実験レベルに当たる.

　前述した通り, 観測データ(outcome)に含まれ得るバイアス(系統誤差)を制御する上で, 統計的手法を処方できるタイミングは実験の前後で2回あった.

　繰り返しになるが, バイアス調整の手段は, 実験前におけるサンプルの割付時点や無作為化によってできる限り交絡(バイアス)を除く方法と, 実験後に統計解析(回帰分析など)を用いてバイアスによる効果を推定する方法に分類できる.

　よって本題であるCIも, 「実験後に統計解析のアプローチによって交絡(系統誤差)を推定する」という区分にカテゴライズされる. ただここがCIに臨む上で誤解を生みやすい部分でもある. ※詳しくはこちらの議論を参考にしてほしい

　後述するが結局CIでも, 適切な対照群のデータを用意することが, 因果推論の信頼性(精度)を高めることに繋がる. その際, 対照群の選定では, 想定される共変量(交絡)を均一化しておくような配慮が望まれる. ※後ほど共変量(covariate)に対照群のデータを扱う

##3. 潜在的アウトカム(反事実)と欠測データ解析

　ここでは準実験レベルにおいて観察データが手に入った後工程である, 欠測データ解析(因果推論)に話を移す.

　CIの実装に移る前に, CIの考え方の原理をinputするために因果推論を代表するフレームワークの1つ, 「Rubinの因果モデル(Rubin causal model)」に軽く触れる.

　Rubinの因果モデルの基本発想は, あるイベント(治療や政策)の介入効果を測りたい時に, 介入対象となるサンプルにおいて介入した場合の結果($Y_1$)と介入しなかった場合の結果($Y_0$)の両方が手に入れば, 介入効果($Z_{Causality}$)は以下の考え方で求められる, というものである.
　　　　

Z_{Causality} = Y_1 - Y_0

　　
　この時, 介入/非介入における各結果変数$Y_1$と$Y_0$を「潜在的アウトカム」(potential outcome)または「潜在的結果変数」と呼ぶ.

　しかし現実では, 介入/非介入の結果両方が同時に手に入らないという問題が出てくる. つまり, 共変量(共変量分布)に全く偏りのない1個体(サンプル)で観察できるのは潜在的アウトカムのうちどちらか一方に限定される場合がほとんどである.

　この現象を(Holland, 1986)では, 「因果推論の根本問題(The fundamental problem of causal inference)」と呼んだ. これは, 以下のよう表で表されることが多い.

サンプル	介入状況	$Y_1$:介入下での結果変数	$Y_0$:非介入下での結果変数	共変量
A	1	✔️	⁇ ※推論が必要	✔️
B	0	⁇ ※推論が必要	✔️	✔️

　参考までに「因果推論の根本問題」の身近な例として, コロナウイルスにおける政策の効果検証を例に説明を試みる.

　いま「ロックダウン(都市閉鎖)」を実施することで, 「1日あたりのウイルス感染者数」に対する政策効果を測りたい. 政策対象となるのは東京都で, 政策期間は現在を実施前夜の"2020/03/31"と仮定とした上で2020年4月の1ヶ月間とする.

　この時先ほどのRubin Modelをそのまま適応すると, 4月から東京都で実際にこの政策を実施した場合, もう一方の東京都における4月のロックダウンが「なかった場合」という結果を手に入れることができない.

　このように, 基本的に介入/非介入の結果変数のどちらかが「欠測データ」となってしまう. 特に計量経済学などにおいては, この観測できない結果変数の方を「反事実(counterfuctual)」と呼ぶ.

　上記を背景に, 観測できない反実仮想の結果を推定する方法として, ようやくここでDIDやCIなどの「欠測データ解析」が登場するという訳である. 以降では, CIの実装を通して実際に欠測データの推定の具体的な中身を見ていく.

##4. CausalImpactとcovariate(共変量)

###テレビCMの因果効果を推定する

　今回は引っ越し見積もりサービスを題材に, 因果推論の対象となるイベントを「テレビCM(Z:介入効果)」として, テレビCMがサイトのアクセス数を表す「DAU: Daily Active User数(Y:結果変数)」の増加にどれだけ寄与したかを推論していく.

　そこで, 観察データとして「時間」×「空間」の2次元の情報を持つDAUのパネルデータ(厳密には繰り返しクロスセクションデータ)を擬似的にサンプリングして用意した.

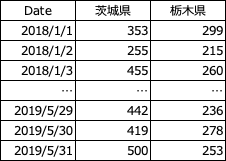
　「時間」については, テレビCMの放映期間を引っ越しの繁忙期である 1月4日~3月31日(2019年) までの約3ヶ月とする. ただし, データとしては2018年1月1日から2019年5月31日までの17ヶ月間のDAUを保持している. ※なお前年の繁忙期にあたる1月4日~3月31日(2018年)のテレビCMは出稿なし

　また「空間」については, 日本の北関東の2県(茨城県・栃木県)を観察対象とする. そしてテレビCMを実際に放映したエリア, つまり介入群(treatment group)となる地域を茨城県とし, 対照群(control group)として栃木県を扱う. ※なおDAUに関してはIPアドレスで各県からのサイトへのアクセス(数)を識別できると仮定した

###library(CausalImpact)

　それでは, 上記のDAUデータ(xlsxファイル)とJupyter NotebookのR環境を準備し, まずはデータをDataFrameとして呼び出す.

# 2県のAUデータをDataFrameとして呼び出す
library(CausalImpact)
library(openxlsx)
dau <- read.xlsx("dau.xlsx")
head(dau)

　次に, 2県のDAUデータを折れ線グラフで可視化する. matplotメソッドはDataFrameのままinputできる.

# 2県のDAUデータを折れ線グラフで可視化
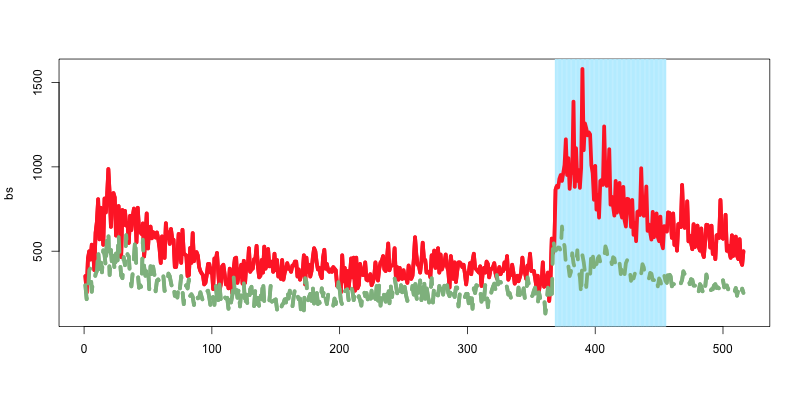
matplot(bs, type="l", lwd=5, col=c("firebrick1", "darkseagreen", "skyblue"))
abline(v=rep(369:455), col="lightblue1", lwd=2, lty=1, alpha=0.1)
matplot(bs, type="l", lwd=5, col=c("firebrick1", "darkseagreen", "skyblue"), add=T)

　※ 赤色: 茨城県, 緑色: 栃木県. またグラフ右側の水色で塗り潰されたの期間が, テレビCMの放映期間を表す

　上記からこの時点で, 2県の結果変数から大きく以下の3点を確認できる.

テレビCM期間のDAUは, 茨城県が栃木県と比べて大きく跳ねている
テレビCM開始前の時点における茨城県と栃木県のDAUの動きが近似している
テレビCMを放映しなかった前年繁忙期(2018年1月~3月)もDAU数のリフトが起きている(≒季節効果の可能性)

###共変量としての対照群のアウトカムがあるとbetterな理由

　次に, 今手に入れたテレビCM期間における茨城県の結果変数(outcome)に含まれるバイアス(交絡)の推定が必要となる.

　CausalImpactでは, 引数dataに結果変数($Y_{(1)}$)と共にcovariate(共変量)をinputすることで交絡因子によるバイアスを加味した反事実(counterfuctual)のデータ系列($Y_{(0)}$)を予測できる.

　その上でまず, CIを利用する上で重要な論点として, 対称群(あるいはそのデータ)を必要とするか否かの議論が存在する. なぜなら, 「CIは, DIDのように対照群を用意しなくても因果推論ができる」という本来の利点と若干矛盾するからだ.

　結論から言うと, 私は後述する「共変量の過不足」という現実的な問題と先述した「実験デザイン」による交絡(バイアス)調整を理由に対照群のデータはあるべきだと考える.

　実際にGoogle社におけるglobalのオペレーションでも, 対称群のデータを共変量(covariate)としてモデルに加えることが推奨されているとのことだった. 彼らからはそうすることでより本来の, 反事実(counterfuctual)のデータを予測するができるというアドバイスを受けた.

　補足すると, 「共変量の過不足」問題については, まず因果推論を行う上で共変量を回帰分析に使う上での2つのハードルを理解する必要がある. 1つ目はそもそも共変量となりうる交絡因子を「特定(認識)」する必要があり, また2つ目は交絡因子を特定できていたとしてそれが「データ」として手に入るかが常にイシューとなる.

　今回の例でいうと, どちらかというと後者がボトルネックとなる. 例えば引っ越し見積もりサイトのアクセス数の共変量として, 「都道府県ごとのある一定期間の引っ越し件数」が考えられる. ただこれがオープンデータとして利用可能か, また結果変数(DAU)と同じく日別(daily)の粒度で存在するかという問題が出てくる.

　また, 「実験デザインの段階で交絡の制御(バイアス調整)に手を打てるなら打つべき」という大原則がCIにも当てはまると理解した. 前述した通り交絡は実験前後のどちらでも対処できるが, 基本的に後のデータ解析に安易に頼ると反事実の推定の負荷が高くなる傾向がある.

　そもそもの目的に立ち返ると, 最終的に予測したかったのは「テレビCMを打たなかった場合の1月4日~3月31日(2019年)の茨城県のDAU($Y_{(0)}$)」だった. なので仮にアクセス数が元々茨城県と類似しており, 考えられる共変量(ある一定期間の引っ越し件数など)の同質性がある程度担保されている都道府県が別に存在するのであれば, そのデータをDID同様の発想で反事実(counterfuctual)として用いることは理に適っている.

　ちなみに上記は, 交絡に対するバイアス調整のうちの「マッチング(共変量分布の均一化)」という手法に該当する. また用意した対照群のマッチングの成否を評価する上では, 介入前の予測残差の大小から共変量としての当てはまりの良さを確認できる.

　以上をまとめると, 結局対照群となる異空間のデータを用意できるのであればそうすることが解析のコストを下げるケースが多いだろう. また, その際に対照群の選定に関しては事前にドメイン知識を元にした共変量とその分布のマッチングを意識できるとなお良い.

　前置きが長くなったが, 実際に結果変数に茨城県のDAU, 共変量に対照群として栃木県のDAUをCausalImpactに入れ, 茨城県におけるテレビCM放映期間の欠測データ($Y_{(0)}$)を予測してみる.

# 結果変数に茨城県のDAU, 共変量に対照群として栃木県のDAUをinputする
pre.period<-c(1,368)
post.period<-c(369,455)
data <- cbind(dau$茨城県, dau$栃木県)

counterfuctualmodel <- CausalImpact(data, pre.period, post.period)
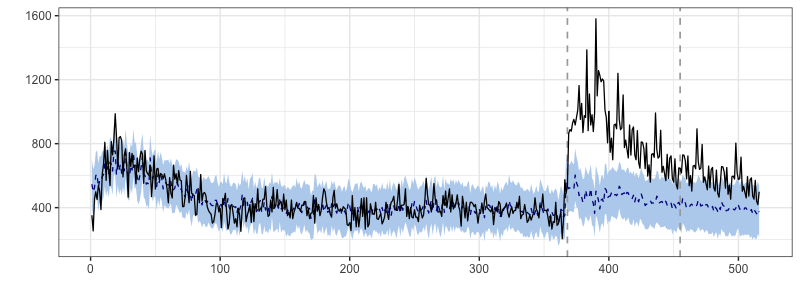
plot(counterfuctualmodel)
summary(counterfuctualmodel)
>> Relative effect (s.d.)   Average: 85% (5.8%) #平均因果効果(増加率)

　上記のグラフの青い点線が反事実のoutcome($Y_{(0)}$)であり, うっすら見える2本のグレーの点線がテレビCMの開始日と終了日, つまり介入期間を表している. 結果として平均因果効果(DAUの増加率)は, 85%だった.

　ただし, いま出力された($Y_{(0)}$)のデータをよくみると, 前年の繁忙期にできていた顕著なリフト(山)が起きていない. これは, バイアス(共変量)として考えられる季節成分を反事実の予測モデルが正確に考慮できていない可能性を示唆している.

##5. 状態空間モデルによる予測精度の向上

　最後の章では, 共変量として考えられる「季節成分(seasonality)」について考えていく. CIのデータ生成のおけるデータの生成過程(DGP: Data Generation Process)を本質的に理解するには, 状態空間モデルを理解する必要がある.

　前提として, CIの論文によるとCausalImpactのデフォルトのモデルは, 状態空間モデルのうち最もシンプルなローカルレベルモデル(local level model)である. 式にすると, 以下で表される.
　　

System:\hspace{1mm} \mu_t \sim Normal(\mu_{t-1}, \sigma^2_\mu)\\
Observed:\hspace{1mm} y_t \sim Normal(\mu_{t}, \sigma^2_y)\\

　　
　ローカルレベルモデルは, ランダムウォーク+ホワイトノイズモデルとも呼ばれ, 状態モデルにおける状態誤差(正規ホワイトノイズ)が累積して状態が変化する. そのため, 状態モデルはランダムウォークとして変化し, 観測モデルはそこに正規分布に従う観測誤差(ホワイトノイズ)が加わった値として最終的な観測値が出力される構造となっている.

　またCIでは, 季節成分やトレンド成分, 共変量に時変回帰係数を含む状態空間モデルであれば, CausalImpactメソッド内のmodel.argsに引数(リスト)を指定するだけで柔軟にモデリングできる.

　一方でより複雑なモデルを組みたいのであれば, RのbstsやKFASなどによるcustomized modelを使えばいいものの, そうするならばそもそもCausalImpactのフレームワーク及びメソッドをあえて使用する必要性はない.

　なお現段階において, 共変量(外生変数)として含まれる栃木県のDAU($x$)が, 観測モデルに不時変である回帰係数$\beta$を持ち存在しているため, 正確な観測モデルは以下となる.
　　

Observed:\hspace{1mm} y_t \sim Normal(\mu_{t}+\beta x_t, \sigma^2_y)\\

　
　いま, ($Y_{(0)}$)における季節成分によるバイアスの推定を行うために, 1年(365日)周期の$\gamma_{Seasonality}$を共変量(説明変数)として観測モデルに加えたい. 周期$k$を持つ時系列データにおける$t$時点の季節成分$\gamma_t$は, 以下の式に従う.
　　

Seasonality\hspace{1mm}System: \hspace{1mm} s_t \sim Normal(0, \sigma^2_s)\\
Seasonality: \hspace{1mm} \gamma_t \sim Normal(-\sum_{i=t-(k-1)}^{t-1}\gamma_i, \sigma^2_s)\\
Observed:\hspace{1mm} y_t \sim Normal(\mu_{t}+\gamma_t+\beta x_t, \sigma^2_y)\\

　　
　なおCausalImpactでは, model.argsにnseasonsを指定することで簡単に周期成分を追加できる.

# 1年周期の*seasonality*を共変量として加える
counterfuctualmodel365 <- CausalImpact(data, pre.period, post.period, model.args=list(nseasons=365))
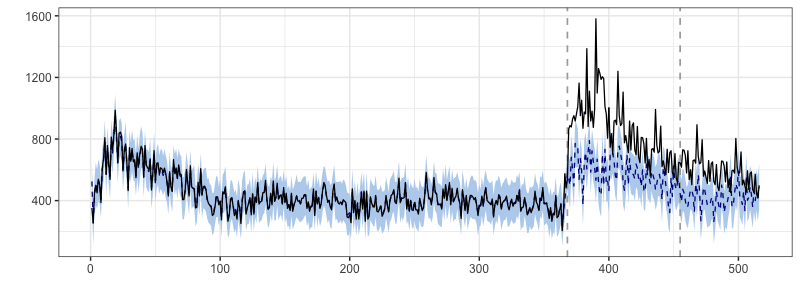
plot(counterfuctualmodel365, "original")
summary(counterfuctualmodel365)
>> Relative effect (s.d.)   49% (3.6%)

　先ほどと比べると, 繁忙期(季節効果)におけるDAUのリフトがより前年のものと近くなったのがわかる. 実際に平均因果効果(DAUの増加率)は, 49%と推定された. seasonalityを加える以前は85%だったので, 繁忙期要因によるバイアスを因果効果の推定量から取り除くことができたとする.

　よって, 因果効果の推定結果としては「テレビCM(介入)によって, +49%のDAU増加効果がもたらされた」とされる.

# 予測残差(*pointwise*)と累積効果(*cumulative*)も確認する
plot(counterfuctualmodel365)

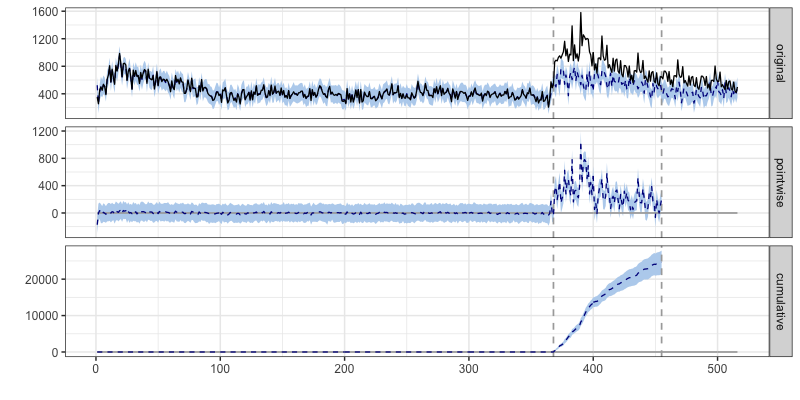
　最後に, 介入前の予測残差(真ん中のpointwiseのグラフ)を確認しても, 当てはまりの良さ(バイアス推定の良し悪し)を確認できる.
　
　以上で, ある程度ドメイン知識と照らしても違和感のない反事実のアウトカムを推定できたので, 今回の効果測定(因果推論)を終える. ご存知の通り, counterfuctualとなる結果変数(欠測データ)の推定に正解はないところもまた難しい.

#結論

　最後に, タイトルにあるCausalImpactという因果推論のフレームワークを利用する上での要所をまとめる.

CIでは, 適切な対照群(共変量のマッチング)のデータをcovariate(共変量)として用意することが推奨されている
時系列データが季節性(seasonality)を持つ場合は, nseasonsで周期を指定すると推定の精度が上がる可能性がある
推定における共変量の良し悪しの判断は, 「介入前の予測残差(plot(,"pointwise"))」に注目することで検証できる

　また, 物事の理解にも適切なアルゴリズム(学習手順)が大切になる. 統計的因果推論の全体観からCausalImpactのポジションを理解するためには, 以下3つの周辺情報を先に抑えることをお勧めする.

統計的因果推論では, 観察されたアウトカムから引き算する「バイアス(系統誤差)」を推定する
バイアスの中でも「交絡(共変量)」は, 実験の前後で調整する手段(実験デザイン or 統計解析)がある
実験後におけるバイアス調整とは「欠測データの予測」であり, いかに現実と近い推定ができるかが勝負である

　CausalImpactは簡単なようで, 前提が深いため因果推論の歴史を時系列で理解した上で利用していきたいと改めて実感した. 次回は, 欠落変数バイアスを扱い, 操作変数法(IV法)と2段階回帰分析法(TSLS)に触れる.

##参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up