2018/04/17 追記

なんと、imbalanced-learnにありました(´・ω・`)
公式ドキュメント
imbalanced-learnのBalancedBaggingClassifierの検証を追記したのでそちらも見て下さい。
ここからジャンプできるよ

はじめに

ざっくり不均衡データへの対応方法まとめ

不均衡データの分類問題を解くとき、適切に調整をしないと大体の場合、良いモデルができません。
不均衡データへのアプローチとしては大きく2種類あります。

①機械学習モデル作成時に重み付けする
手法によっては、学習時に数の少ないデータの重みを上げることで不均衡データに対応することができます。
scikit-learnのRandomForestClassifierでいえば、パラメータclass_weightがそれにあたります。

②データ量を調整する
そもそもモデルに学習させるデータ量を調整するアプローチです。
少ないデータを増やすオーバーサンプリングと、多いデータを減らすアンダーサンプリングの2種類があります。（どちらも同時に行うこともある）
オーバーサンプリングについては本記事では扱いませんが、下記に超簡単にまとめます。

オーバーサンプリング
- 数の少ないデータを複製して増やす
  簡単だけど同じデータが増えるから過学習しがち
- SMOTE
  いい感じに数の少ないデータを増やしてくれるアルゴリズム

アンダーサンプリングは、数が多いデータをランダム抽出して数を減らすアプローチですが、せっかくのデータを捨ててしまうことになるのでそのまま使うと残念になりがちです。
そこで、アンダーサンプリングとバギングを組み合わせるといい感じに学習できることが分かっています。

バギング is 何
ざっくり言うと複数のモデルを並列につくって、ブートストラップサンプリングしたデータでそれぞれ学習する手法です。
いろんなモデルをバギングでアンサンブルして精度を高めるために使われたりします。
決定木をバギング（+特徴量もランダム）するとランダムフォレストになります。
余談ですが、予測結果を返す方法にはhard votingとsoft votingの二種類があります。
- hard voting : 単純に多数決です。10個のモデルのうち7つがA、3つがBって言ったらAを予測結果として返します。
- soft voting : 各モデルの予測確率の平均を取ります。

すなわち、バギングのブートストラップサンプリング時にアンダーサンプリングを行うことで、不均衡データに対応することができます。
上記の各手法については、書籍やWebで賢い方々が解説してくれているので詳しく知りたい方はそちらをどうぞ。

PyPIに登録したよ

本題です。
アンダーサンプリング＋バギングは、残念ながらsci-kit learnとかimblearnを探しても見つかりませんでした。
普段sci-kit learnのAPI叩くマンの僕としては悲しかったので、実装してPyPIに登録しました。
つかいたい方は下記のようにしてpip installしてください。

pip install usbclassifier

pythonで使うときは下記みたいにimportしてね。
一応sklearnチックなメソッドにしてます。

from usbclassifier import USBaggingClassifier

とりあえずソースコードみたい人はGithubへどうぞ。
以降では、二値分類と他クラス分類それぞれにおいて、

ランダムフォレスト
重み付けランダムフォレスト
アンダーサンプリング＋バギング（分類器：ランダムフォレスト）

の3手法のときの決定境界を可視化して、各手法の性能を見てみます。
下記の検証用ソースコードはこちら（Jupyter notebook）
とりあえずpip installして、↑のGitダウンロードしてJupyter notebook実行すれば再現できる（はず）

二値分類

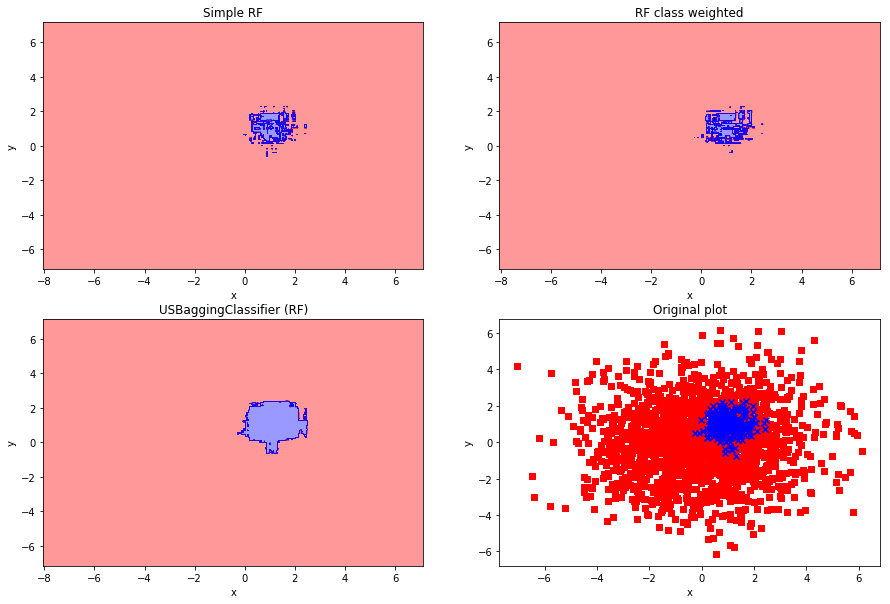
250個の負例と1750個の正例の二値分類問題を、上述の3手法でpredictしたときの決定境界を書いてみます。
データは二次元の正規分布で適当につくります。

# read csv
binary_toy = pd.read_csv(os.path.join(data_dir, 'binary_toydata.csv'))

X = np.array(binary_toy.drop('response', axis=1))
y = np.array(binary_toy.response)

# Simple Random Forest
rf_model = RandomForestClassifier(n_jobs=-1)
rf_model.fit(X, y)
plt.figure(figsize=[15,10])
plt.subplot(221)
visualize_utils.plot_decision_regions(X, y, rf_model, only_regions=True)
plt.title('Simple RF')

# Weighted Random Forest
rf_model = RandomForestClassifier(class_weight='balanced', n_jobs=-1)
rf_model.fit(X, y)
plt.subplot(222)
visualize_utils.plot_decision_regions(X, y, rf_model,only_regions=True)
plt.title('RF class weighted')

# USBaggingClassifier
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='soft')
X_df = binary_toy.drop('response', axis=1)
y_ss = binary_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(223)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF)')

# original plot
plt.subplot(224)
positive = binary_toy[binary_toy.response == 1]
negative = binary_toy[binary_toy.response == 0]
plt.scatter(negative.feature_x, negative.feature_y, c='red',marker='s')
plt.scatter(positive.feature_x, positive.feature_y, c='blue',marker='x')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Original plot')

右下の図がデータの散布図です。
単純なランダムフォレストでは、決定境界がつぶつぶになって過学習感がすごいですね。
また、重み付けランダムフォレストで予測した右上の図も同様です。
それらと比較して、アンダーサンプリング＋バギングで予測した左下の図では、なんだか汎化性能高そうな境界ができてます。
やったー。

他クラス分類

今度は他クラス分類です。
データ個数は(3750, 250, 250, 250, 250)の5クラス分類をやってみましょう。

# read_csv
multi_toy = pd.read_csv(os.path.join(data_dir, 'multi_toydata.csv'))
X = np.array(multi_toy.drop('response', axis=1))
y = np.array(multi_toy.response)

# Simple Random Forest
rf_model = RandomForestClassifier(n_jobs=-1)
rf_model.fit(X, y)
plt.figure(figsize=[15,10])
plt.subplot(221)
visualize_utils.plot_decision_regions(X, y, rf_model, only_regions=True)
plt.title('Simple RF')

# Weighted Random Forest
rf_model = RandomForestClassifier(class_weight='balanced', n_jobs=-1)
rf_model.fit(X, y)
plt.subplot(222)
visualize_utils.plot_decision_regions(X, y, rf_model,only_regions=True)
plt.title('RF class weighted')

# USBaggingClassifier
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='hard')
X_df = multi_toy.drop('response', axis=1)
y_ss = multi_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(223)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF)')

# original plot
plt.subplot(224)
for i, color, marker in zip(multi_toy.response.value_counts().index.tolist(),
                            ('red', 'blue', 'gray', 'cyan', 'lightgreen'), 
                            ('s', 'x', 'o', '^', 'v')):
    one_class_df = multi_toy[multi_toy.response == i]
    plt.scatter(one_class_df.feature_x, one_class_df.feature_y, c=color, marker=marker)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Original plot')

二値分類のときと同様の結果になりました。
良いですね、アンダーサンプリング＋バギング。

BalancedBaggingClassifierの検証

imblearnのBalancedBaggingClassifierで、同じことができますorz
パラメータ:ratioを'not minority'にすることで、一番少ないラベル以外をアンダーサンプリングした上でバギングしてくれます。
上記と同様の検証を、BalancedBaggingClassifierでやってみましょう。

二値分類

# read csv
binary_toy = pd.read_csv(os.path.join(data_dir, 'binary_toydata.csv'))

X = np.array(binary_toy.drop('response', axis=1))
y = np.array(binary_toy.response)

# Simple Random Forest
rf_model = RandomForestClassifier(n_jobs=-1)
rf_model.fit(X, y)
plt.figure(figsize=[15,20])
plt.subplot(321)
visualize_utils.plot_decision_regions(X, y, rf_model, only_regions=True)
plt.title('Simple RF')

# Weighted Random Forest
rf_model = RandomForestClassifier(class_weight='balanced', n_jobs=-1)
rf_model.fit(X, y)
plt.subplot(322)
visualize_utils.plot_decision_regions(X, y, rf_model,only_regions=True)
plt.title('RF class weighted')

# USBaggingClassifier soft voting
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='soft')
X_df = binary_toy.drop('response', axis=1)
y_ss = binary_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(323)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF) Voting="soft"')

# USBaggingClassifier hard voting
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='hard')
X_df = binary_toy.drop('response', axis=1)
y_ss = binary_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(324)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF) Voting="hard"')

# BalancedBagingClassifier
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = BalancedBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, ratio='not minority')
usbc.fit(X, y)
plt.subplot(325)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('BalancedBaggingClassifier (RF)')

# original plot
plt.subplot(326)
positive = binary_toy[binary_toy.response == 1]
negative = binary_toy[binary_toy.response == 0]
plt.scatter(negative.feature_x, negative.feature_y, c='red',marker='s')
plt.scatter(positive.feature_x, positive.feature_y, c='blue',marker='x')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Original plot')

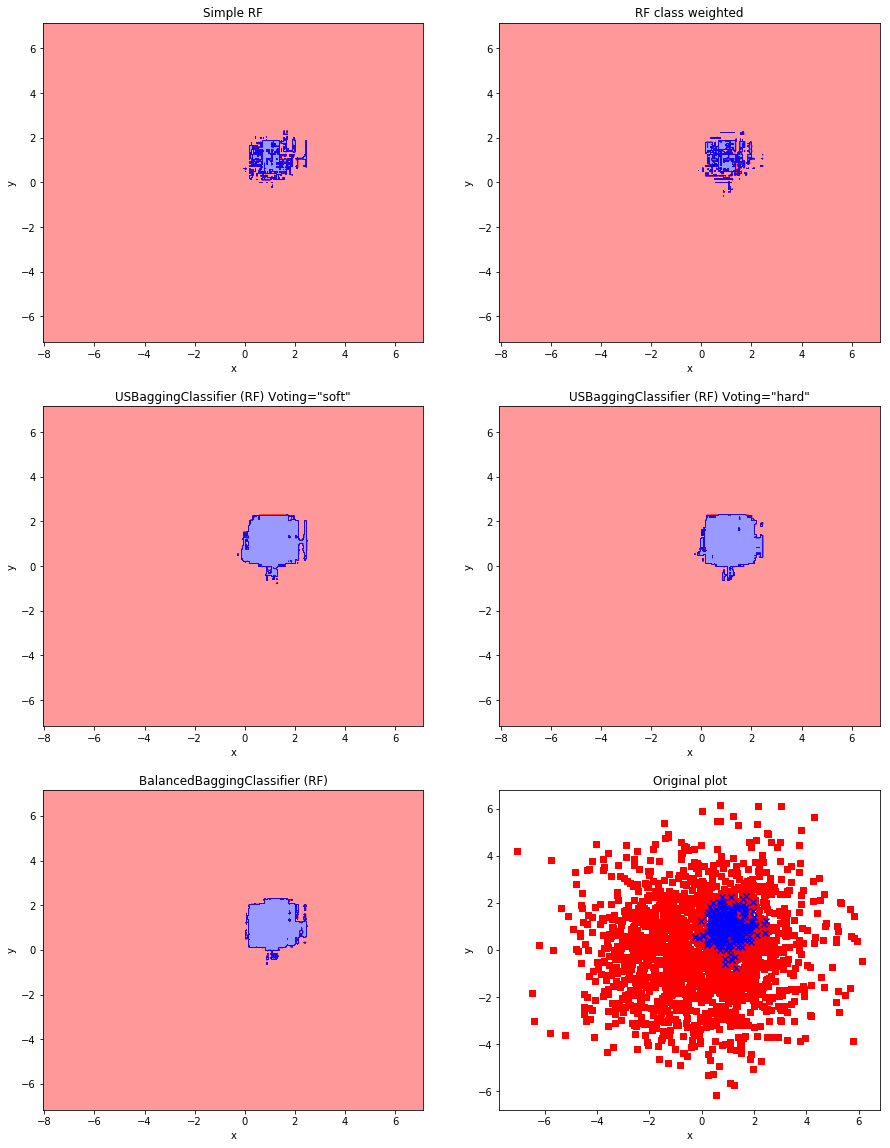
当たり前ですが、BalancedBaggingClassifierでちゃんとアンダーサンプリング＋バギングの効果を確認できますね。
ぼくの実装したUSBaggingClassifierでは、Votingをsoftとhard選べるので、2つの結果を載せてみました。
imblearnのBalanced~は（てかsklearnのBaggingClassifierもですが）モデルがpredict_probaメソッドを持ってない場合hard voting、持っている場合はsoft votingする仕様なので、その点は僕のパッケージの方がいいですね。（白目）
完全なる四角い車輪の再発明じゃないと思いたい・・・
でも、よっぽどの理由がない限りimblearnを使ったほうが良いと思います。
よっぽどの理由：imblearnやsklearnのバージョンに制約があってBalancedBaggingClassifierが使えないとか

他クラス分類

# read_csv
multi_toy = pd.read_csv(os.path.join(data_dir, 'multi_toydata.csv'))
X = np.array(multi_toy.drop('response', axis=1))
y = np.array(multi_toy.response)

# Simple Random Forest
rf_model = RandomForestClassifier(n_jobs=-1)
rf_model.fit(X, y)
plt.figure(figsize=[15,20])
plt.subplot(321)
visualize_utils.plot_decision_regions(X, y, rf_model, only_regions=True)
plt.title('Simple RF')

# Weighted Random Forest
rf_model = RandomForestClassifier(class_weight='balanced', n_jobs=-1)
rf_model.fit(X, y)
plt.subplot(322)
visualize_utils.plot_decision_regions(X, y, rf_model,only_regions=True)
plt.title('RF class weighted')

# USBaggingClassifier soft voting
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='soft')
X_df = multi_toy.drop('response', axis=1)
y_ss = multi_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(323)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF) Voting="soft"')

# USBaggingClassifier hard voting
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = USBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, voting='hard')
X_df = multi_toy.drop('response', axis=1)
y_ss = multi_toy.response
usbc.fit(X_df, y_ss)
plt.subplot(324)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('USBaggingClassifier (RF) Voting="hard"')

# BalancedBagingClassifier
rf_model = RandomForestClassifier(n_jobs=-1)
usbc = BalancedBaggingClassifier(base_estimator=rf_model, n_jobs=-1, n_estimators=10, ratio='not minority')
usbc.fit(X, y)
plt.subplot(325)
visualize_utils.plot_decision_regions(X, y, usbc,only_regions=True)
plt.title('BalancedBaggingClassifier (RF)')

# original plot
plt.subplot(326)
for i, color, marker in zip(multi_toy.response.value_counts().index.tolist(),
                            ('red', 'blue', 'gray', 'cyan', 'lightgreen'), 
                            ('s', 'x', 'o', '^', 'v')):
    one_class_df = multi_toy[multi_toy.response == i]
    plt.scatter(one_class_df.feature_x, one_class_df.feature_y, c=color, marker=marker)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Original plot')

他クラス分類でも同様です。

おわりに

実際に決定境界を見てみることで、アンダーサンプリング＋バギングが良い方法であることがよく分かりました。
そして、重み付けランダムフォレストが全然だめだったのが衝撃でした。
(勿論パラメータ調整の余地はあるけど)

PyPIで公開している上記USBaggingClassifierですが、
inputするX,yにnp.arrayが使えない（DataframeとSeriesのみ）などなどクソい部分は多々あるので、是非プルリクエストください（他力本願）
最後まで読んでいただき、ありがとうございました。

参考文献

Python機械学習プログラミング
最近第二版が出た良書。決定領域の可視化スクリプトは本書を参考にしました。
前処理大全
先日出た良書。サンプリングまわりの話はこちらを参照しました。
https://tjo.hatenablog.com/entry/2017/08/11/162057
ちょっと前の良ブログ。Rでアンダーサンプリング＋バギングの決定領域を可視化しています。（めっちゃ参考にしました）

[Python]不均衡データ分類問題に対する定番アプローチ：under sampling + baggingを実装したよ

2018/04/17 追記

はじめに

ざっくり不均衡データへの対応方法まとめ

PyPIに登録したよ

二値分類

他クラス分類

BalancedBaggingClassifierの検証

二値分類

他クラス分類

おわりに

参考文献