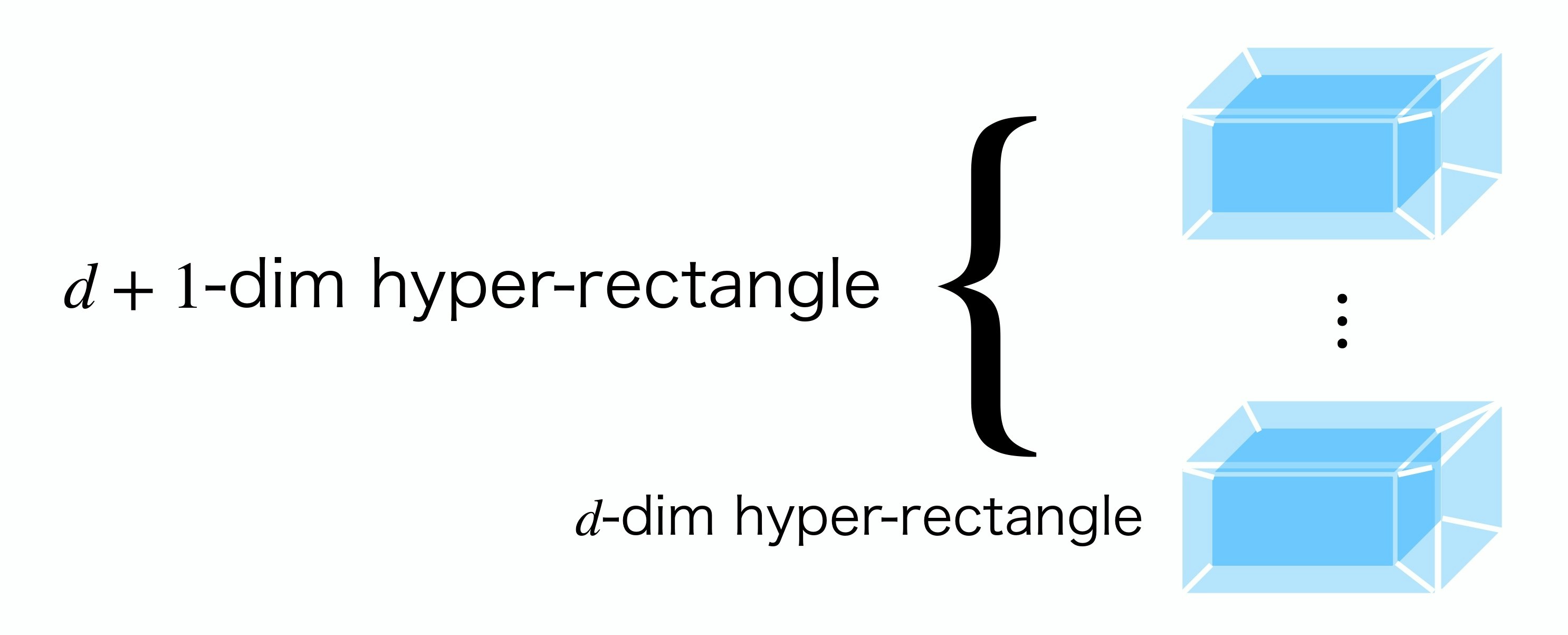
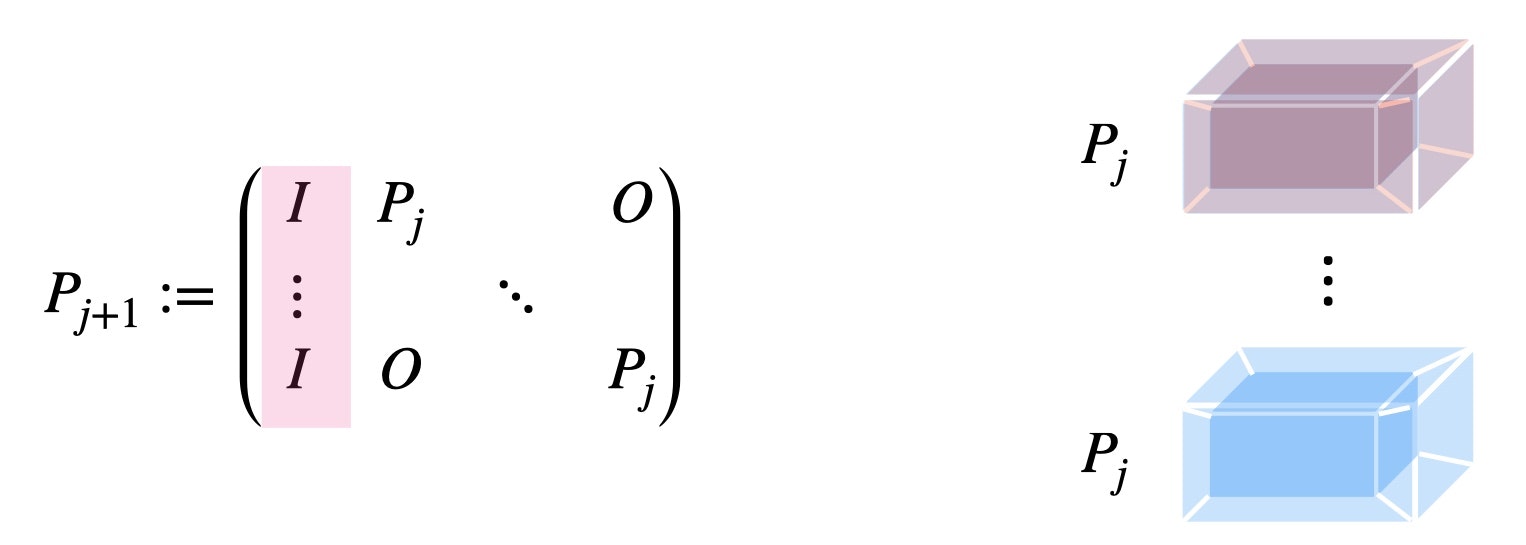はじめに
ルービックキューブのような3次元立方体パズルを$d$次元に一般化した時の解空間をCoq/SSReflectで形式検証します。
ソースはこちら
スライドはこちら
問題
元ネタはこちらTPPmark2025
n≥1 を整数とする.同じサイズの立方体型ランプを隙間なく n^3 個並べて,全体として n×n×n の大きな立方体を作る.
すると,その外面には各面に n×n 個,計 6n^2 個の小正方形(外側に見えているランプの外面)が現れる. 各ランプは on/off のいずれかの状態をもち,外面の小正方形のうち一つを押すと,その小正方形とちょうど反対側にある小正方形を結ぶ直線上(*1)の n 個のランプだけが同時に反転(on↔off)する.
全ランプの on/off の状態が与えられたとき,上記の操作の繰り返しのみですべてのランプを off にできるための必要十分条件をなるべく簡潔に記述し,その条件の正しさを証明せよ.
(*1) 追記(2025/9/16):「その小正方形とちょうど反対側にある小正方形を結ぶ直線上」は「その小正方形を垂直に貫通する直線上」の意です.
考え方
この問題はルービックキューブに似ているので、ルービックキューブと同様に考えていきます。
実際にルービックキューブは有限非可換体の部分群だと考えられるので、これも同様に代数学に当てはめて考えます。今回の場合は可換群になるのでルービックキューブよりも簡単に解けそうです。さらに各ランプの状態はon/offの2値、すなわち有限体なので、線形代数のベクトル空間で書けそうです。そう思うとこれは別に3次元立方体である必要がなさそうです。
そこで本記事ではこれを一般化して$d$次元$n_0\times\cdots\times n_{d-1}$超直方体にして、さらに状態も一般化してon/offだけでなくある性質を満たす一般の体の場合について考察していきます。
各種定義
まずは数式の上で$n_0\times\cdots\times n_{d-1}$超直方体についていきます。($n_0,\,\ldots,\,n_{d-1} \in \mathbb{N}$)
以降
I_n := \{0,\,\ldots,\,n-1\}
とします。
ランプの座標
各ランプの集合は$\displaystyle\prod_{i=0}^{d-1}I_{n_i}$で表せます。
以下の図の黄色い超立方体がランプです。
表面
表面ですが、超直方体から1次元除いた空間、すなわち、k次元目のベクトルと直交する1つの表面は$\displaystyle\prod_{i\neq k}I_{n_i}$で表せます。
つまりk次元方向のベクトルの直交補空間が表面になるということです。
よって表面のスイッチ全体の集合は全ての
次元の方向$k < d$に対する表面の和である$\displaystyle\sum_{k = 0}^{d-1}\prod_{i\neq k}I_{n_i}$で表せます。
(表面には表と裏がありますが、ボタンとしての役割が同じなのでこの問題においては同一視してもよい)
ただし、これだとCoqで実装する時に型の関係で使いづらいので、表面の集合$\operatorname{surface}$を以下のように定義します。
\operatorname{surface} := (I_d \times \prod_{i = 0}^{d-1}I_{n_i})/\sim
ここで"$/ \sim$"は同値類を表し、同値関係$\sim$を以下のように定義します。
(x_0,x_1) \sim (y_0,y_1) := x_0 = y_0 \wedge \forall k, k \neq x_0 \to x_1 \,k = y_1\,k
これが$\displaystyle\sum_{k = 0}^{d-1}\prod_{i\neq k}I_{n_i}$と1対1対応することは全単射の存在性から分かります。
実際に、
f : (I_d \times \prod_{i=0}^{d-1}I_{n_i})/ \sim \to \sum_{k=0}^{d-1}\prod_{i \neq k}I_{n_i}
f\,(k,(x_0,\,\ldots,\,x_{d-1})) := (x_0,\,\ldots,\,x_{k-1},\,x_{k+1},\,\ldots,\,x_{d-1})
と定義するととwell-definedとなり、今、任意の$i$に対して$n_i \neq 0$を仮定しているので
g : \sum_{k=0}^{d-1}\prod_{i \neq k}I_{n_i} \to (I_d \times \prod_{i=0}^{d-1}I_{n_i})/ \sim
g\,(x_0,\,\ldots,\,x_{k-1},\,x_{k+1},\,\ldots,\,x_{d-1}) :=
(k,(x_0,\,\ldots,\,x_{k-1},\,0,\,x_{k+1},\,\ldots,\,x_{d-1})) :=
とおけば$f \circ g = \operatorname{id}$かつ$g \circ f = \operatorname{id}$となります。
各ランプの状態
ここではランプの状態の集合を素数$p$に対する位数$p$の有限体$\mathbb{F}_p := \{0,\,\ldots,\,p-1\}$で考えます。
なぜ$\mathbb{F}_p$を考えるかというと、次の性質を満たす体$K$の必要十分条件だからです。
\forall x \in K, \exists n \in \mathbb{N}, x = n*1_K
これは体$K$上の演算$+$に対して巡回群になっていることを表しています。
この条件は後に線形代数を使うのに使います。
もちろんon/offの2値の場合は$p=2$の時の$\mathbb{F}_2$を考えれば良いです。
全てのライトの状態
全てのライトの状態$\operatorname{state}$は以下のように表せます。
\operatorname{state} := \prod_{i=0}^{d-1}I_{n_i} \to \mathbb{F}_p
これを後に以下のように有限次元ベクトルに変換します。
\mathbb{F}_p^{\prod_{i=0}^{d-1}n_i}
表面のスイッチ
表面のスイッチですが、以下のような型になります。
\operatorname{switch} : \operatorname{surface} \to \operatorname{state} \to \operatorname{state}
この初期状態$\operatorname{init}$に対し、全てのランプをOFFにできることは次の式で表せます。
\exists l:\operatorname{surface}^*, \operatorname{foldr}\,\operatorname{switch}\,\operatorname{init}\,l = 0
問題はそのスイッチの実装ですが、
表面の各スイッチはその直交する1次元ベクトルのランプの状態のみを変化させます。
具体的には、表面$(k,(x_0,\,\ldots,\,x_{d-1}))$のスイッチを押したときに変化するランプの座標は$(x_0,\,\ldots,\,x_{k-1},\,i,\,x_{k+1},\,\ldots,\,x_{d-1})$で書き表せます。ただし$i$は$i < n_k$を満たす任意の値です。
スイッチを押した時にこれらの座標のランプの状態を$1_{\mathbb{F}_p}$増やします。
これをベクトルで表したものを$v \in \mathbb{F}^{\prod_{i=0}^{d-1}n_i}$とすると、スイッチを押す前の状態をベクトルで表したものが$s$の時、スイッチを押すことで状態が$s + v$に変化するということです。
すなわち、全てのランプをOFFにできるということを
\exists l:\operatorname{surface}^* \sum_{x \in l} f_d\,x + \operatorname{init} = 0
と書けるということです。
今、表面は有限集合なので、有限列$l$に登場する表面$x$の個数を$m_x$とおくと
\exists m:\operatorname{surface} \to \mathbb{N}, \sum_{x \in l} m_x * f_d\,x + \operatorname{init} = 0
とかけます。さらに$\mathbb{F}_p$が$+$に関して巡回群であるため$m_x * f_d\,x = a f_d\,x$となる$a \in \mathbb{F}_p$が存在するので
\exists m:\operatorname{surface} \to \mathbb{F}_p, \sum_{x \in l} m_x * f_d\,x +
\operatorname{init} = 0
すなわち
\exists m:\operatorname{surface} \to \mathbb{F}_p, \sum_{x \in l} -m_x * f_d\,x =
\operatorname{init}
とかけます。これはまさに線型空間に入っていることを表しています。
しかしながらこのスイッチを押した時のベクトルの具体的な式はどう表せばいいのでしょうか?
スイッチをベクトルで表す
上記のように表面のスイッチを押した時に変化する量をベクトルで表したもの全体の集合
\displaystyle V_{n_0,\,\ldots,\,n_{d-1}} \subset \mathbb{F}_p^{\prod_{i=0}^{d-1}n_i}
を次元に関する再帰で定義します。
すなわち上の図で言う$\operatorname{Im}f_d$を次元に関する再帰で定義します。
0次元のとき
0次元超直方体には表面が存在しないので$V_\emptyset := \emptyset$とします。
j+1次元のとき
超直方体の次元を増やすということは、以下のような図で表せます。
$V_{n_0,\,\ldots,\,n_{j-1}}$は有限集合であるので、この要素を全て並べて行列にしたものを
P_j : \mathbb{F}_p^{|\operatorname{surface}| \times \prod_{i=0}^{j-1}n_i}
と置くことができます。このとき、$P_{j+1}$は次の行列で表せます。
具体的に見ていきましょう。
まず、次元の1つ小さい超直方体は下図の緑色の箇所に対応します。
表面ですが、下図の黄色の位置の場合はこのベクトルに対応します。
下図の赤色のような新たに出来た次元の表面に対するベクトルはこれです。
これによって$V_{n_0,\,\ldots,\,n_{d-1}}$が定義できました。
ランプが全てOFFになるとき
ランプが全てOFFになることと同値な命題を示します。
上でも述べたようにランプの初期状態をベクトルに変換したものを$x_0$と置いたとき、
上で定義した$V_{n_0,\,\ldots,\,n_{d-1}}$を使って以下のように書けます。
x_0 \in <V_{n_0,\,\ldots,\,n_{d-1}}>
スイッチを押すことはこれらのベクトルの足すことに他ならないので、有限回スイッチを押してOFFにできることは線型空間に含まれていることと同値になります。
線型空間の基底
上でランプが全てOFFになることと、ランプの初期状態$x_0$が超直方体の構造から定義される線型空間$<V_{n_0,\,\ldots,\,n_{d-1}}>$に入っていることと同値になることが分かりました。
そこでこのベクトル空間の基底を再帰的に求めます。
$0$次元のときは$0$次元ベクトル空間なので基底なしです。
$j$次元の時のベクトル空間の基底を並べて行列にしたものを$B_j$と置いたとき、
$j+1$次元の時のベクトル空間の基底を並べて行列にしたものは次のように表せます。
B_{j+1} :=
\begin{pmatrix} I & B_j & & O\\
\vdots & & \ddots & \\
I & 0 & & B_j\\
I & 0 & \cdots & 0\end{pmatrix}
上の$P_{j+1}$の定義から一次従属のベクトル
\begin{pmatrix} O\\ \vdots\\ O\\ P_j\end{pmatrix}
を除いたものになり、これで一時独立性、すなわち基底であることが言えます。
このベクトル空間の次元$\dim<B_j>$は$B_j$の列ベクトルの個数になるので、次の漸化式を満たします。
\dim<B_0>=0
\dim<B_{j+1}> = \prod_{i=0}^{j} n_i + (n_{j+1} -1)\dim<B_j>
これを解くと
\dim<B_d> = \prod_{i=0}^d n_i - \prod_{i=0}^d (n_i - 1)
となります。
Coqでの定義
これをCoqで形式化してみます。
まず、$d$次元超直方体は各次元の辺の長さのリストs:seq natで表します。
ランプの座標
まず、ランプの座標$\displaystyle\prod_{i=0}^{d-1}I_{n_i}$を定義します。
Definition hyperspace (s:seq nat) :=
foldr (fun n T => prod_finType (ordinal_finType n) T) unit_finType s.
(* foldr (prod \o ordinal) unit s *)
後にこれがfintypeであることを使う関係でややこしい定義になっていますが
実際にはfoldr (prod \o ordinal) unit sです。
表面
表面$(I_d \times \prod_{i = 0}^{d-1}I_{n_i})/\sim$は以下のように定義します。
Definition surface (s:seq nat) :=
prod_finType (ordinal_finType (size s)) (hyperspace s).
(* 'I_(size s) * hyperspace s. *)
これもfintypeであることを使うために定義がややこしいですが、実質的には'I_(size s) * hyperspace sです。
同値類$\sim$の部分ですが、特に定義はせず同値類を取らない形で定義しています。
理由としては、表面が命題で登場するのがexists p:seq (surface s)の形であるからです。
任意の集合$X$とその上の同値類$\sim$に対して、$X$上の述語$P:X \to 2$が$\sim$
に対してwell-defined、すなわち任意の$a \sim b$に対し$P\,a \leftrightarrow P\,b$を満たすならば$\exists x \in X / \sim, P\,x \leftrightarrow \exists x \in X, P\,x$が成り立つからです。
ランプの状態
1つのランプの状態を体K:fieldTypeで表したとき、全てのランプの状態
$\prod_{i=0}^{d-1}I_{n_i} \to K$は次のように定義します。
Definition state (s:seq nat) : Type := {ffun hyperspace s -> K}.
ここで体Kの満たすべき仮定$\forall x \in K, \exists n \in \mathbb{N}, x = n*1_K$を定義しておきます。
Definition cyclic_K := forall x:K, exists n, x = (n%:R)%R.
表面のスイッチ
表面のスイッチを押した時の状態の変化switch:surface s -> state s -> state sを次のように定義します。
Fixpoint switch_rec (s:seq nat) (n:nat) :
hyperspace s -> state s -> state s :=
match s,n return hyperspace s -> state s -> state s with
| [::], _ => fun _ => id
| _ :: s', 0 => fun c t =>
[ffun x => if (x.2 == c.2) then (t x + 1)%R else t x]
| _ :: s', n'.+1 => fun c t =>
[ffun x =>
if x.1 == c.1
then switch_rec n' c.2 [ffun y => t (x.1,y)] x.2
else t x]
end.
Definition switch (s:seq nat) (b:surface s) : state s -> state s :=
switch_rec b.1 b.2.
表面を次元の方向($I_d$で何番目の次元かを表す)と座標に分離して座標の次元に対して帰納的に定義します。
具体的にはこの座標と一致する座標と、それと次元の方向上にある全ての座標(つまりスイッチによって変化する全ての座標に1を足します。
これは前に定義した同値関係$\sim$が成り立つ2つの値を第一引数に入れると関数として同値になり、well-definedになります。
この時、ランプの初期init:state sが与えられたとき、全てのランプがOFFになるようなスイッチの押す順番が存在することは以下のように定義できます。
Definition execute (s:seq nat) (p:seq (surface s)) : state s -> state s :=
foldr (comp \o @switch _) id p.
Definition reachable (s:seq nat) (init:state s) : Prop :=
exists p:seq (surface s), execute p init = [ffun => 0%R].
ベクトルの世界で表現する
これらをベクトルの世界で記述します。
使用するライブラリはmathcompのssralg.vector.vです。
まず、state sをfoldr muln 1 s次元のvectTypeに型変換する関数state2vecを定義します。
Definition exp2v (n:nat) (x:K ^ n) :
exp_vectType (regular_vectType _) n := x.
Fixpoint ord2hyperspace (s:seq nat) : 'I_(foldr muln 1 s) -> hyperspace s :=
match s return 'I_(foldr muln 1 s) -> hyperspace s with
| [::] => fun => tt
| _ :: _ => fun x => let: (x1, x2) := unmulord x in (x1, ord2hyperspace x2)
end.
Definition state2vec (s:seq nat) (t:state s) :
exp_vectType _ (foldr muln 1 s) := exp2v [ffun x => t (ord2hyperspace x)].
ここで途中に$\prod_{i=0}^d I_i$を$I_{\prod_{i=0}^d i}$に変換していることがわかると思います。
これが1対1対応であることを次を満たす逆関数vec2stateを定義することで証明します。
Lemma state2vecK (s:seq nat): cancel (@state2vec s) (@vec2state _).
Lemma vec2stateK (s:seq nat): cancel (@vec2state s) (@state2vec _).
次に表面のスイッチを押すことをベクトルの和で表現したいので、表面のスイッチをベクトルに変換する関数surface2vecを定義します。
Fixpoint surface2state_rec (s:seq nat) (n:nat) : hyperspace s -> state s :=
match s,n return hyperspace s -> state s with
| [::], _ => fun _ => [ffun => 0%R]
| _ :: s', 0 => fun c => [ffun x => if (x.2 == c.2) then 1%R else 0%R]
| _ :: s', n'.+1 => fun c =>
[ffun x => if (x.1 == c.1)
then surface2state_rec n' c.2 x.2 else 0%R]
end.
Definition surface2state (s:seq nat) (c:surface s) : state s :=
surface2state_rec c.1 c.2.
Notation surface2vec c := (state2vec (surface2state c)).
一旦stateの型に変換することで定義しています。
この時スイッチを押すことと、これらをベクトルに変換して足したものが一致することが以下の定理より示せます。
Lemma state2vec_switch (s:seq nat) (c:surface s) (t:state s):
state2vec (switch c t) = (state2vec t + surface2vec c)%R.
このことから表面のベクトル列と初期状態のベクトルの和が0になることと
スイッチを全てOFFにできることが同値になります。
Definition vreachable' (s:seq nat) (init:state s) :=
exists (p:seq (surface s)),
(\sum_(c <- p) surface2vec c + state2vec init)%R = 0%R.
Lemma reachableP' (s:seq nat) (init:state s) :
reachable init <-> vreachable' init.
決定可能関数で表現する
上の命題ではあくまでPropを返す形で決定可能な命題の形ではないです。
そこで、これをベクトル空間に所属しているかどうかで表現することで決定可能な命題でかけます。
Definition cyclic_K := forall x:K, exists n, x = (n%:R)%R.
(* Hcyclic K <-> #| K | is prime i.e. K ~ F_p *)
Definition vreachable (s:seq nat) (init:state s) :=
state2vec init \in (\sum_(c in surface s) <[surface2vec c]>)%VS.
Lemma reachableP (s:seq nat) (init:state s):
cyclic_K -> reflect (reachable init) (vreachable init).
reflectで書けるということはvreachable initがboolであるということです。
しかしながら(\sum_(c in surface s) <[surface2vec c]>)%VSの部分が冗長なので基底を求めていきます。
基底を求める
基底のベクトル列を求める関数basisは次のようになります。
Fixpoint statebasis (s:seq nat) : seq (state s) :=
match s return seq (state s) with
| [::] => [::]
| n :: s' => (if n is S _
then codom (fun c => [ffun x => if x.2 == c then 1%R else 0%R])
else [::])
++ flatten
[seq map
(fun f:state s' =>
[ffun x => if val x.1 == i then f x.2 else 0%R])
(statebasis s') | i <- iota 0 n.-1]
end.
Notation basis s := [seq state2vec x | x <- statebasis s].
これが基底になっていることは次の命題で示せます。
Lemma free_basis (s:seq nat): free (basis s).
freeが一次独立性を表す述語で、これは次元に関する帰納法で示します。
このベクトル空間に初期状態が入っていることと全てのランプをOFFにできることは次の命題で示せます。
Lemma basis_reachable (s:seq nat) (init:state s):
cyclic_K -> reflect (reachable init) (state2vec init \in <<basis s>>%VS).
<<X>>%VSがベクトルのリストXが生成する線型空間を表します。
これで形式化ができました。
ちなみにこのベクトル空間の次元は次のように示せます。
Lemma dim_basis (s:seq nat):
\dim <<basis s>>%VS = \prod_(n <- s) n - \prod_(n <- s) n.-1.
まさに
\dim<B_d> = \prod_{i=0}^d n_i - \prod_{i=0}^d (n_i - 1)
を表しています。
元の問題に適用する
$d=3$, $\{n_0,n_1,n_2\} = \{n,n,n\}$の場合を考えればいいので
解空間の次元は$n^3-(n-1)^3$になります。
まとめ
TPPmark2025の問題を一般化したものをCoq/SSRefrectで形式化しました。