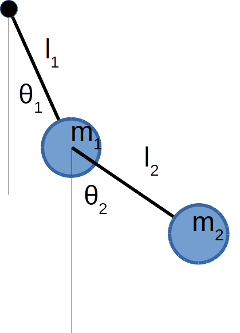
二重振り子とは
以前にsympyで運動方程式という記事でsympyを使ってバネ・ダンパ系の運動方程式の導出をやったのですが、今回は二重振り子の運動方程式を導出したいと思います。
二重振り子は物理の力学ではよく出てくるもので、下図のように振り子の先にさらに振り子がついています。振り子が二重になっただけなのですが、単振り子とは比べ物にならないくらい複雑な動きをするので、カオスや複雑系などの話にもよく出てきます。
数式
まずは単振り子の運動方程式を見てます。(上の図で振り子が1つになっているのをイメージしてください。)
ml\ddot{\theta} + mg \sin\theta = 0
1項目が慣性項、2項目が重力項を表していて、振り子の角加速度がそのときの振り子の角度の$\sin$に比例している関係であることが分かります。
次に二重振り子です。真面目に導出するとなると、ラグランジュ関数を用いて…と長い話になってしまうので、今回は式の確認のためにWikipediaからサクッと取ってきます。
(m_1+m_2)l_1\ddot{\theta}_1 + m_2l_2\ddot{\theta}_2\cos(\theta_1 - \theta_2) + m_2l_2\dot{\theta}_2^2\sin(\theta_1 - \theta_2) + (m_1 + m_2)g\sin\theta_1 = 0
\\\
l_1l_2\ddot{\theta}_1\cos(\theta_1- \theta_2) + l_2^2\ddot{\theta}_2 - l_1l_2\dot{\theta}_1^2\sin(\theta_1 - \theta_2) + gl_2\sin\theta_2 = 0
式を見ただけでも、単振り子の運動方程式と比較してかなり複雑になっていることが分かると思います。
SymPyBotics
前回はSymPyのphysics.mechanicsモジュールを直接使って数式の導出を行ったのですが、今回のような剛体が節(リンク)で接続された物体の場合にさらに簡単に数式の導出が行えるSymPyBoticsを用いてみたいと思います。
githubから取ってきてインストールします。
git clone https://github.com/cdsousa/SymPyBotics.git
cd SymPyBotics
sudo python setup.py install
SymPyBoticsを用いて、二重振り子を作成します。
以下がそのコードです。
import sympybotics
rbtdef = sympybotics.RobotDef('Double Pendulum',
[(0, 'l_1', 0, 'q-pi/2'),
(0, 'l_2', 0, 'q')],
dh_convention='standard')
from sympy import symbols, Matrix, simplify, pprint
g = symbols('g')
rbtdef.gravityacc = Matrix([[0.0],[-g],[0.0]])
rbt = sympybotics.RobotDynCode(rbtdef)
for p in rbt.geo.p:
pprint(simplify(p), use_unicode=False)
sympybotics.RobotDefを呼び出しているところが二重振り子を作成しているところになります。[(0, 'l_1', 0, 'q'),(0, 'l_2', 0, 'q')]が実際の二重振り子のパラメタになるのですが、Denavit–Hartenbergパラメタと呼ばれるロボットで用いられるパラメタの与え方になっています。簡単に説明するとl_1,l_2が振り子1と振り子2の長さ、qは振り子の角度を示しており、振り子作成後にq1,q2という変数に割り当てられます。1つ目の角度がq1-pi/2になっていますが、これは角度をどこから測るかを調節するために加えています。図ではy軸負から角度を測っているのに対し、SymPyBoticsはx軸正から角度を測るようになっているためです。
三重振り子にしたい場合は[(0, 'l_1', 0, 'q-pi/2'),(0, 'l_2', 0, 'q'),(0, 'l_3', 0, 'q')]となります。
最後に書いているプリントは振り子の位置を表す式を出力しており、以下のようになります。
[l_1*sin(q1) ]
[ ]
[-l_1*cos(q1)]
[ ]
[ 0 ]
[l_1*sin(q1) + l_2*sin(q1 + q2) ]
[ ]
[-l_1*cos(q1) - l_2*cos(q1 + q2)]
[ ]
[ 0 ]
rbt.dyn.gen_all()
params = {'l_1x': 0.0, 'l_1y': 0.0,
'l_2x': 0.0, 'l_2y': 0.0,
'L_1zz': 0.0, 'L_2zz': 0.0}
mass = simplify(rbt.dyn.M.subs(params))
corioli = simplify(rbt.dyn.c.subs(params))
gravity = simplify(rbt.dyn.g.subs(params))
次に運動方程式の要素となるそれぞれの項(慣性項、遠心・コリオリ力項、重力項)を導出します。rbt.dyn.gen_all()で生成し、今回不要なパラメタ(慣性モーメントに関わるパラメタ)を消去します。
eq = (mass * rbtdef.ddq + corioli + gravity).as_mutable()
eq[0, 0] -= eq[1, 0]
params = {rbtdef.ddq[1, 0]: rbtdef.ddq[1, 0] - rbtdef.ddq[0, 0],
rbtdef.dq[1, 0]: rbtdef.dq[1, 0] - rbtdef.dq[0, 0],
rbtdef.q[1, 0]: rbtdef.q[1, 0] - rbtdef.q[0, 0]}
print simplify(eq.subs(params))
最後に、実際に運動方程式を計算します。最初の行の時点で運動方程式は導出されているのですが、Wikipediaと結果を照らし合わせるために式の簡略化と変数の変更を行っています。
Matrix([
[l_1*(\ddot{q}_1*l_1*m_1 + \ddot{q}_1*l_1*m_2 + \ddot{q}_2*l_2*m_2*cos(q1 - q2) + \dot{q}_2**2*l_2*m_2*sin(q1 - q2) + g*m_1*sin(q1) + g*m_2*sin(q1))],
[ l_2*m_2*(\ddot{q}_1*l_1*cos(q1 - q2) + \ddot{q}_2*l_2 - \dot{q}_1**2*l_1*sin(q1 - q2) + g*sin(q2))]])
少し見にくいですが、式がイコール0だと考えて不要な変数を除去すると、Wikipediaの二重振り子の運動方程式と一致しているのが分かると思います。
今回は二重振り子でしたが、他にも多重振り子やロボットなどの運動方程式導出に応用できそうです。