sympyで運動方程式

sympyで運動方程式

pythonの数式処理ライブラリのsympyで物理で出てくる運動方程式を扱えるようなので、試してみたいと思います。
今回は参考サイトのpydy_exampleの中にもあるマス・バネ・ダンパ系の運動方程式を導出するスクリプトを書いてみます。
まず、図に示すようなマス・バネ・ダンパ系があるとします。普通に運動方程式を立てると以下のようになります。

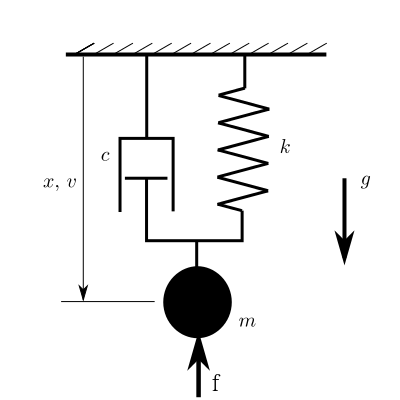
運動方程式

{\bf M}\dot{{\bf x}} = {\bf f}({\bf x})

ここで

{\bf x} = [{\it x}, \dot{{\it x}}]^T \\
{\bf M} = \begin{bmatrix} 1 & 0 \\ 0 & m \end{bmatrix} \\
{\bf f}({\bf x}) = \begin{bmatrix} \dot{x} \\ -k x - c \dot{x} + m g + f \end{bmatrix}

であるとします。
次にスクリプトです。sympy.physics.mechanicsというモジュールを使います。Kane's methodというのを使って運動方程式を立てているのですが、これがイマイチよく分かりません。ラグランジュ法で解く方法もあるようです。

mass_spring_dumper.py

#!/usr/bin/python
#coding:utf-8
import sympy as sym
import sympy.physics.mechanics as me

x, v = me.dynamicsymbols('x v')
m, c, k, g, t, f = sym.symbols('m c k g t f')

# 座標系の作成
ceiling = me.ReferenceFrame('C')

o = me.Point('o') # 天井の点
p = me.Point('p') # 質点
o.set_vel(ceiling, 0)
p.set_pos(o, x * ceiling.x)
p.set_vel(ceiling, v * ceiling.x)

# 質点にかかる外力を計算
damping = -c * p.vel(ceiling) # ダンピング
stiffness = -k * p.pos_from(o) # バネ
gravity = m * g * ceiling.x # 重力
exf = f * ceiling.x # その他の外力

forces = damping + stiffness + gravity + exf
print forces

mass = me.Particle('mass', p, m)
kane = me.KanesMethod(ceiling, q_ind=[x], u_ind=[v], kd_eqs=[v - x.diff(t)])
kane.kanes_equations([(p, forces)], [mass])
M = kane.mass_matrix_full
f = kane.forcing_full
print M
print f
print M.inv() * f

出力は以下のようになります。

(-c*v + f + g*m - k*x)*C.x
Matrix([[1, 0], [0, m]])
Matrix([[v(t)], [-c*v(t) + f + g*m - k*x(t)]])
Matrix([[v(t)], [(-c*v(t) + f + g*m - k*x(t))/m]])

使い方を勉強すればかなり強力なツールになりそうです。
力学系の式を立ててくれるソフトは有料ではmapleやmathematicaがありますが、いずれも高価なので、このようなソフトがフリーで使えるのはありがたいですね。

参考サイト

sympyドキュメント http://docs.sympy.org/latest/index.html
pydy examples https://github.com/PythonDynamics/pydy_examples