学習目標
線形回帰(Linear Regression)で仮説を立てる理由について理解する
Hypothesis(仮説)の線を作る
正解に近い仮説を特定できるCost Functionについて理解する
用語説明
| 用語 | 説明 |
|---|---|
| Linear Regression | 線形回帰 |
| Hypothesis | 仮説 |
| 用語 | 説明 |
|---|---|
| H(x) | 仮説(Hypothesis) |
| Wx | 傾斜(W(なんの略か不明確warpかな)) |
| b | 偏差(bias) |
線形回帰(Linear Regression)で仮説を立てる理由
シンプルに説明するため、以下のようなトレーニングデータを用意しました。
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
これを線形に表現すると以下のようになります。
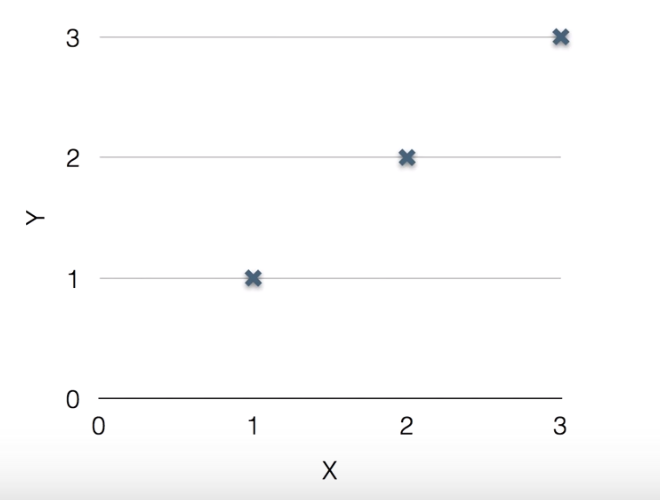
世の中にこのような線形で予測できるものがたくさんがあります。
たとえば、以下のようなものです。
家の家賃を予想したい場合(家が広いほど、家賃が高い)
試験の成績を予想したい場合(勉強に与えた時間が多いほど、成績が高い)
などなどです。
仮説の線を立てる方法
それでは仮説を立てる線を作ってみましょう
トレーニングデータのxと任意のデータ
W,bを入れて作ります。
式では以下のように書きます。
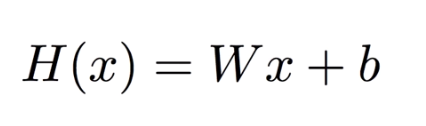
Cost Functionとは
以下の図は三つの仮説を立てて線形にしたものです。
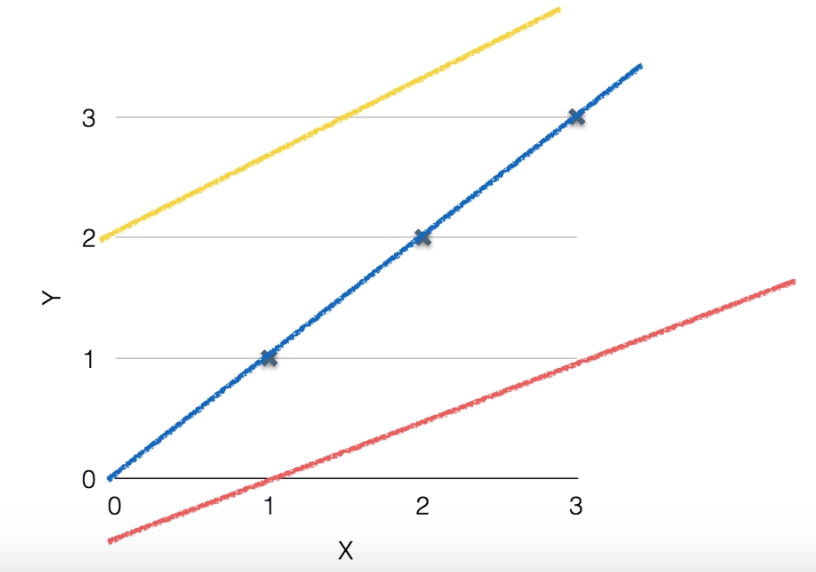
トレーニングデータがx=1,y=1, x=2,y=2, x=3,y=3のため
目でみると青い線がトレーニングデータに当てはまるのがわかります。(仮説も三つしかないし)
でも俺らはパソコンにわかってもらえるように数学的に求める方法が必要です。
そのため、Cost Functionというものを利用します。
Cost Functionとは大雑把に言うと
「仮説で立てた線」と「正解の線」の立ての距離(y)を比べてその距離が短ければ短いほど正解の線だろう特定することです。
以下図のように立ての距離を比較します。
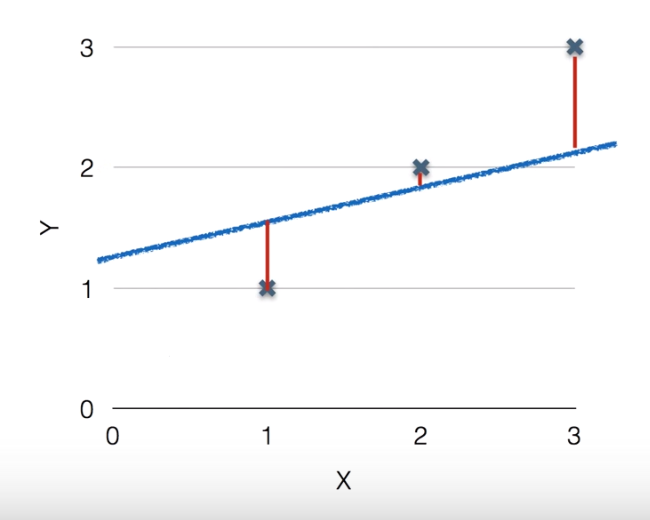
「仮説で立てた線」 - 「立ての距離(y)」なので
今言ったことを式で書くと以下のようになります。
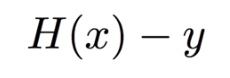
ただ、これだと
仮説で立てた線よりyが大きければ
マイナスになってしまうので二乗をします。
※二乗することで+、ーと関係なく正数のデータを出せるし差が多ければペナルティーを与えることが可能です。
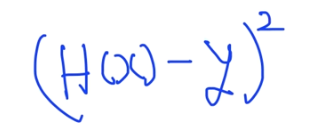
この式を今回のトレーニングデータに適用してみると以下のようになります
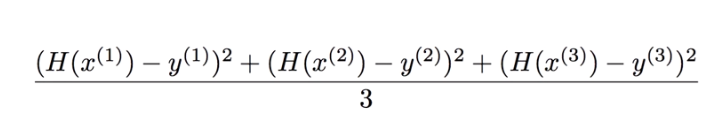
トレーニングデータは三つのため3で割りました。
何百万件のトレーニングデータにも使える式で表現するには以下のように表現します。
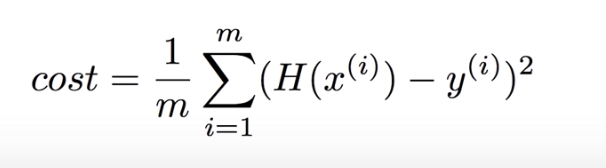
ここでHは
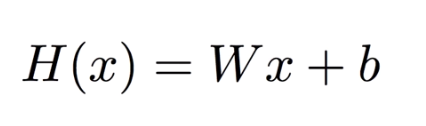
の結果でしたよね
ので以下のようにも表現できると思います。
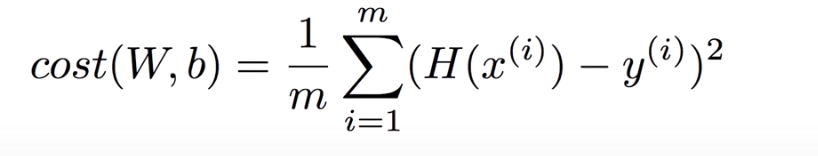
また、このcostの値(W,b)が小さければ小さいほど正解に近い仮説を特定することが可能です。
よって以下のように表現します。
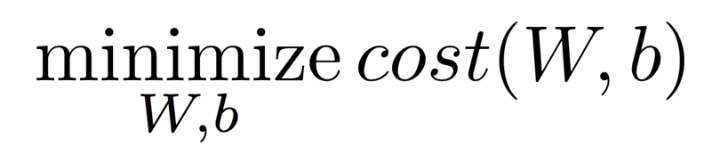
ここまでの結論
トレーニングデータと任意のW,b値を利用して仮説の線を作る
Cost(W,b)の値が小さければ小さいほど正解の線に近い