はじめに
Panasonic のアドベントカレンダー1発目の記事です。
最近 AtCoder でコンテストを開催しまくりと話題の Panasonic です。
自社コンテストの開催は本当に嬉しいもので、テンションがブチ上がった勢いで社内SNSに競プロのコミュニティを作りました!...ほとんど何もできず、放置気味です。すみません。
さすがに申し訳なく感じ、社内のエンジニアに競プロを布教する用の資料を細々と用意していました。そんなときにアドカレの話を聞きつけ、せっかくなので一般向けに書こうと思い立ち、今に至ります。
目的
パナソニックプログラミングコンテスト(sponsored by Panasonic 含む、以下 パナコン)の問題を通して、競プロの面白さを感じてもらう ことを目的としています。「競プロ入門」「競プロ上達」などに関しては素晴らしい記事が既に存在するため、ここではそれらを紹介するにとどめます。
想定読者
元々が社内向け想定だったこともあり、基本的なプログラミング経験がある方 を対象としています(記事中では Python3を使用します)。AtCoder のアカウントを用意 していただけると、より楽しめると思います!
競技プログラミング(競プロ)とは?
ある問いに対し、どれだけ早く最適な答えをプログラミングで導き出せるか、あるいは時間内にどれだけ多くの答えを出せるかを競う競技です。(引用)
早速ですが、例題を見てみましょう。
実行時間制限: 2 sec
問題文
$N$ 個の整数 $A_1,A_2,...,A_N$ が与えられます。
$1 \leq i < j \le N$ を満たす全ての $(i,j)$ の組についての $\left| A_i - A_j \right|$ の和を求めてください。
制約
$・2 \leq N \leq 2 \times 10^5$
$・\left|A_i\right| \leq 10^8$
$・$ 入力は全て整数
入力形式
$N$
$A_1\ A_2\ ...\ A_N$
出力
答えを出力せよ。
(出題元)
要するに
- 配列の要素数を入力から受け取る
- 配列を入力から受け取る
- 配列の要素の全ペアの"差の絶対値"の和を求める
を実現するプログラムを作成する問題です。
例えば入力が
3
5 1 2
であれば、
全ペア $(5, 1),\ (5, 2),\ (1, 2)$ について差の絶対値を計算し、
$\left|5-1\right| + \left|5-2\right| + \left|1-2\right| = 8$ を出力します。
プログラミング経験者であれば、まずはこのような解法を思いつくでしょう。
N = int(input()) # 整数の入力
A = list(map(int, input().split())) # 整数配列の入力
ans = 0
for i in range(0, N-1):
for j in range(i+1, N):
ans += abs(A[i] - A[j])
print(ans) # 答えの出力
for文を2重 に使用して全ペアの差の絶対値を計算し、それを足し合わせています。問題の指示内容をそのまま実装した形のプログラムですね。確かにこれは正しいプログラムです。
% python sample.py
3 # 入力: N
5 1 2 # 入力: A1 A2 A3
8 # 出力: 答え
「...これの何が面白いの?」と思うかもしれません。
安心してください。このプログラムを提出しても、1点ももらえません。先に少しネタバラシをすると、2重forループでは計算に時間がかかり、$N$ が大きいときに実行時間制限(2秒)を超過してしまうのです。試しに $N = 10^5$ 程度の入力を与えてみると、プログラムが一向に終了せず PC のファンが暴走し始めます。
このような 愚直で非効率な解法だと正解にならない のが競プロの面白さ です。アルゴリズム/データ構造の知識、数学的思考、パズル的思考 などを駆使し、十分に効率が良い解法を考えて実装することで初めて正解となります。
それでは、ここから順を追って説明していきますので、この問題にはまた後で登場してもらいましょう。
(忙しい人用のショートカット -> こちら)
AtCoder Beginner Contest (ABC)の紹介
↑の例題は、 パナソニックプログラミングコンテスト(AtCoder Beginner Contest 186)で出題された問題です。
「AtCoder Beginner Contest(ABC)」
ほぼ毎週、土曜 or 日曜の 21:00~22:40 に開催されるコンテスト。簡単な問題(A問題)から高難度問題(H問題)まで8問出題される。
特に最初は、この ABC への参加がメイン になります。
「Beginner 向けかよ...」と侮ってはいけません。現在の ABC を時間内に全完できる競プロerはごくわずかです。名前とは裏腹に、初心者から上級者まで楽しめるコンテストです。
簡単な問題であっても、早く(速く)正確に解く必要があります。ぜひリアルタイムでコンテストに参加して、競プロerの問題を解くスピードを体感してください。次々と順位表が埋まっていく光景に、私は心が挫けそうになりました。
パナコン(ABC) の問題を解いてみよう!
それでは、実際に ABC の問題を解いて、競プロの面白さを体感してみましょう!
パナソニックプログラミングコンテスト(sponsored by Panasonic 含む) にて出題された問題をいくつかピックアップしました。一部の問題は、徐々にヒントを出していく形式で紹介するので、ぜひ実際に頭と手を動かしながら読んでください!
注1)パナコンは全て ABC として開催されています。
注2)問題タイトルは、引用元へのリンクになっています。
A - Brick
実行時間制限: 2 sec
問題文
トラックが $1$ 台あります。このトラックには合計で $N$ キログラム以下の荷物を載せることができます。このトラックに、$1$ 個 $W$ キログラムのレンガを最大でいくつ載せることができますか?
制約
$・1 \leq N,W \leq 1000$
$・N,W$ は整数である。
入力形式
$N$ $W$
出力
トラックに載せることができるレンガの個数の最大値を整数で出力せよ。
まずはウォーミングアップ。
A問題は、標準入力、基本的な演算、if文 などが使えれば問題ありません。
**(答えはここを click!)**
$N$ を $W$ で割った商(余り切り捨て)を出力すればOKです。n, w = map(int, input().split()) # N W を入力
ans = n//w
print(ans) # 答えを出力
言語によっては標準入力が複雑なので、調べておきましょう。
この問題では面白みを感じないと思いますが、AtCoder 上で提出して AC(Accepted, 正解)と表示された瞬間の気持ちよさを味わってみてください!
B - Many Oranges
実行時間制限: 2 sec
問題文
みかんがたくさんあります。どのみかんの重さも $A$ グラム以上 $B$ グラム以下であることがわかっています。(みかんの重さは整数とは限りません。)
この中からいくつかのみかんを選んだところ、選んだみかんの重さの合計がちょうど $W$ キログラムになりました。
選んだみかんの個数として考えられる最小値と最大値を求めてください。
ただし、このようなことが起こり得ないなら、UNSATISFIABLEと出力してください。
制約
$・1 \leq A \leq B \leq 1000$
$・1 \leq W \leq 1000$
$・$ 入力は全て整数
入力形式
$A$ $B$ $W$
出力
選んだみかんの個数としてありえる最小値と最大値を空白区切りでこの順に出力せよ。ただし、与えられた条件に合うような個数が存在しない場合、かわりに
UNSATISFIABLEと出力せよ。
まずは単位を合わせるため、$W$ に $1000$ をかけておきます。
(以下、$W$ は $1000$ をかけたものとして扱います。)
例えば、
$(A,B,W)=(6,9,25)$ のとき、$(8,8,9)$ や $(7,9,9)$ で個数を最小、$(6,6,6,7)$ で個数を最大にできるので、答えは $3$ と $4$ です。
$(A,B,W)=(6,8,17)$ のとき、どう組み合わせても 合計を $17$ にできません。
(簡単のため、実際の入力ではありえない $W$ の例で考えています。)
よく考えれば、割り算、切り上げ/切り捨て、if文 を使って解けるのですが、やや複雑です。
実はこの問題は、競プロの基本中の基本である 全探索 を使うとスッキリ解くことができます!
「全探索」
全てのありえるパターンを探索するアルゴリズム。例えば「答えとしてあり得る値を全部調べる」など。
この問題を全探索で解いてみましょう。
一発で思いつくのは難しいので、ヒントを小出しにしていきます。
**(ヒント 1)**
「重さ $A$ 以上 $B$ 以下のみかんを **ちょうど $N$ 個使って** 重さ合計 $W$ にできるか?」は、どのように判定できるでしょうか?**(ヒント 2)**
$A=1,\ W=1000000\ (=10^6)$ のとき、みかんの個数の最大値は $10^6$ 個です。この問題の答えが、これを超えることはありません。**(ヒント 3)**
ヒント 1 の $N$ を $1$ から $10^6$ まで全探索することで、答えが求められないでしょうか?**(答えはここを click!)**
「重さ $A$ 以上 $B$ 以下のミカンを ちょうど $N$ 個使って 重さ合計 $W$ にできるか?」を調べるには、$AN \leq W \leq BN $ であるかを判定すればよいです。
ありえそうな全ての $N$ について、この判定を行いましょう。
$A$ が最小の $1$、$W$ が最大の $10^6$ のとき、$10^6$ 個 のみかんを選ぶことができます。この問題では、これを超える個数のみかんを選べることはないので、$N$ としてありえる値は $1$ から $10^6$ です。
よって、$1 \leq N \leq 10^6$ について、「重さ $A$ 以上 $B$ 以下のミカンを ちょうど $N$ 個使って 重さ合計 $W$ にできるか?」を調べ、OK だった $N$ の値のうち 最小/最大 を出力することで、この問題を解くことができます!
a, b, w = map(int, input().split())
w *= 1000
ans_min, ans_max = 10**10, -1 # 適当な値で初期化
for n in range(1, 10**6+1): # あり得る N を全探索
if a*n <= w <= b*n: # 条件を満たすか確認
ans_min = min(ans_min, n)
ans_max = max(ans_max, n)
if ans_max == -1: # 条件を満たす N がなかった場合
print('UNSATISFIABLE')
else:
print(ans_min, ans_max)
どれくらいの難易度?
- ABC参加者の約5割強が解ける
- 近年のB問題の中ではダントツで正解者数が少ない(難しい)...
参考
B - Bishop
もう1問、少し毛色の違うB問題を見てみましょう。
(リンク先を直接読んでください。)
これは、多くの競プロerを罠にはめて有名となったB問題です。トップレベルの人たちも、WA(Wrong Answer) を量産していました。サンプルの図を見るとパッと解けそうな問題ですが、解いて提出して罠にかかってみてください。
(公式解説)
C - Swappable
実行時間制限: 2 sec
問題文
$N$個の整数からなる配列 $A=(A_1,A_2,...,A_N)$ が与えられるので、次の条件を全て満たす整数組 $(i,j)$ の数を求めてください。
・$1 \leq i \leq j \leq N $
・$A_i \neq A_j$
制約
$・$ 入力は全て整数
$・2 \leq N \leq 3 \times 10^5$
$・1 \leq A_i \leq 10^9$
入力形式
$N$
$A_1 \ A_2 \ ... \ A_N$
出力
答えを整数として出力せよ。
「配列の要素の全ペアのうち、値が異なるものの個数」を答える問題です。
今回も 「全ペアを確認して条件を満たすものを数える」全探索が使えそう に見えます。
N = int(input())
A = list(map(int, input().split())) # 配列の入力
ans = 0
for i in range(0, N-1):
for j in range(i+1, N):
if A[i] != A[j]: # 条件を満たすか?
ans += 1
print(ans)
2重 for ループを使ったプログラムです。
しかし、このプログラムを提出すると TLE(実行制限時間超過)となってしまいました。

実行制限時間
競プロの問題には実行時間制限があり、AtCoderでは多くの問題が 2秒 です。目安として、ループ回数が $10^8$ を大きく超えてくるようなプログラムは TLE になる可能性が高いです。
この問題の制約では $2 \leq N \leq 3 \times 10^5$ であり、全ペア $\frac{N(N-1)}{2}$ 通りの全探索(2重ループ)では $N$ が大きい時に $10^{10}$ を超えるほどのループ数となるため、余裕の TLE です。(上のスクショでは実行時間が 2208 ms となっていますが、TLE すると途中で実行が打ち切られるため、実際にはもっと時間がかかります。)
「2重ループしたいけどできない...」という問題はかなり頻繁に見かけます(どうしても2重ループになる動画)。
(補足) 計算量を考える
厳密にループ回数を求めるのは面倒なので、実際には 計算量 を考えることである程度の実行時間を見積もります。
$N \leq 10^5$ 程度の問題では、$O(N)$ や $(NlogN)$ の解法で解くことが多いです。
高速なアルゴリズムを考え直す
では、2重forループにならないような解法を考えましょう。
**(ヒント)**
$A_i \neq A_j$ なるペアを直接数えるのではなく、 $A_i = A_j$ なるペアを数えて全体から引くことを考えましょう。**(答えはここを click!)**
全ペア $(i,j)$ のうち、$A_i \neq A_j$ ではなく、$A_i = A_j$ となるものを数えます。
全ペア $\frac{N(N-1)}{2}$ 通りから $A_i = A_j$ となるものを引けば、$A_i \neq A_j$ なるペアの個数が得られます。
では、$A_i = A_j$ なるペアの求め方はどうすればいいでしょうか。
これは、それぞれの数が何回出現したか を数えることで計算することができます。$v$ という数が $m$ 回出現したなら、 $v$ 同士のペアは ${}_m C_2 = \frac{m(m-1)}{2}$ 個つくることができます。配列の全要素を確認し、それぞれの数の出現回数をカウントし、最後にまとめてこの計算をしてしまいましょう。
数のカウントには、Python なら dict、C++ なら map (unordered_map) を利用できます。
N = int(input())
A = list(map(int, input().split()))
# 数の出現回数をカウント
cnts = {}
for a in A:
cnts.setdefault(a, 0)
cnts[a] += 1
# 同じ数同士のペアは何個作れるか?
eq_cnt = 0
for cnt in cnts.values():
eq_cnt += cnt*(cnt-1)//2
ans = N*(N-1)//2 - eq_cnt
print(ans)
どれくらいの難易度?
- ABC参加者の約7割が解ける
- C問題としては平均より易しい
C - ORXOR
C問題をもう1つ紹介します。
これは bit全探索 と呼ばれる全探索の手法を利用する問題です。エンジニアには馴染みの深い、再帰/深さ優先探索 でも解くことができます。
実装が少しややこしく、C問題の中では正解者数がかなり少なめでした。
D - Sum of difference
実行時間制限: 2 sec
問題文
$N$ 個の整数 $A_1,A_2,...,A_N$ が与えられます。
$1 \leq i < j \le N$ を満たす全ての $(i,j)$ の組についての $\left| A_i - A_j \right|$ の和を求めてください。
制約
$・2 \leq N \leq 2 \times 10^5$
$・\left|A_i\right| \leq 10^8$
$・$ 入力は全て整数
入力形式
$N$
$A_1\ A_2\ ...\ A_N$
出力
答えを出力せよ。
最初に紹介した問題の再登場です。
ここまで読んでくださった方なら、最初に見たときと問題の見え方が変わっているかもしれません。C問題で説明した通り「$N \leq 2 \times 10^5 $ で 2重ループですると余裕で TLE」なので、高速な解法を考えましょう。
**(ヒント 1)**
配列 $A$ の要素を自由に並び替えても、全ペアの差の絶対値の和 に変化はありません。**(ヒント 2)**
大半の言語に標準搭載されている `sort` 関数は、配列の要素を $O(NlogN)$ で昇順(降順)に並び替えることができます。**(ヒント 3)**
配列 $A$ を昇順(降順)に `sort` した後だと、絶対値の記号が外しやすくなりませんか?ここでは2通りの解法を紹介します。どちらも競プロでは頻出の考え方です。
**(答え その 1 はここを click!)**
ヒント 1 の通り、配列 $A$ の要素の順番は自由に入れ替えても答えは変わらないので、昇順に並び替えてみましょう。大半の言語には、$O(NlogN)$ で昇順に並び替えられる sort が標準搭載されています。
sortすることで、「各要素が何番目に大きい値なのか」がわかります。これを利用して絶対値記号を外し、各要素が何回プラス/マイナスされるか を計算してみましょう。
下の例を見てください。絶対値の記号を外すとき、自分より小さな値との差の絶対値ではプラス、自分より大きな値との差の絶対値ではマイナスとなります。
これにより、その要素が 何回プラスされるか/何回マイナスされるか がわかり、答えにどれだけの影響を与えるかを計算する ことができます。
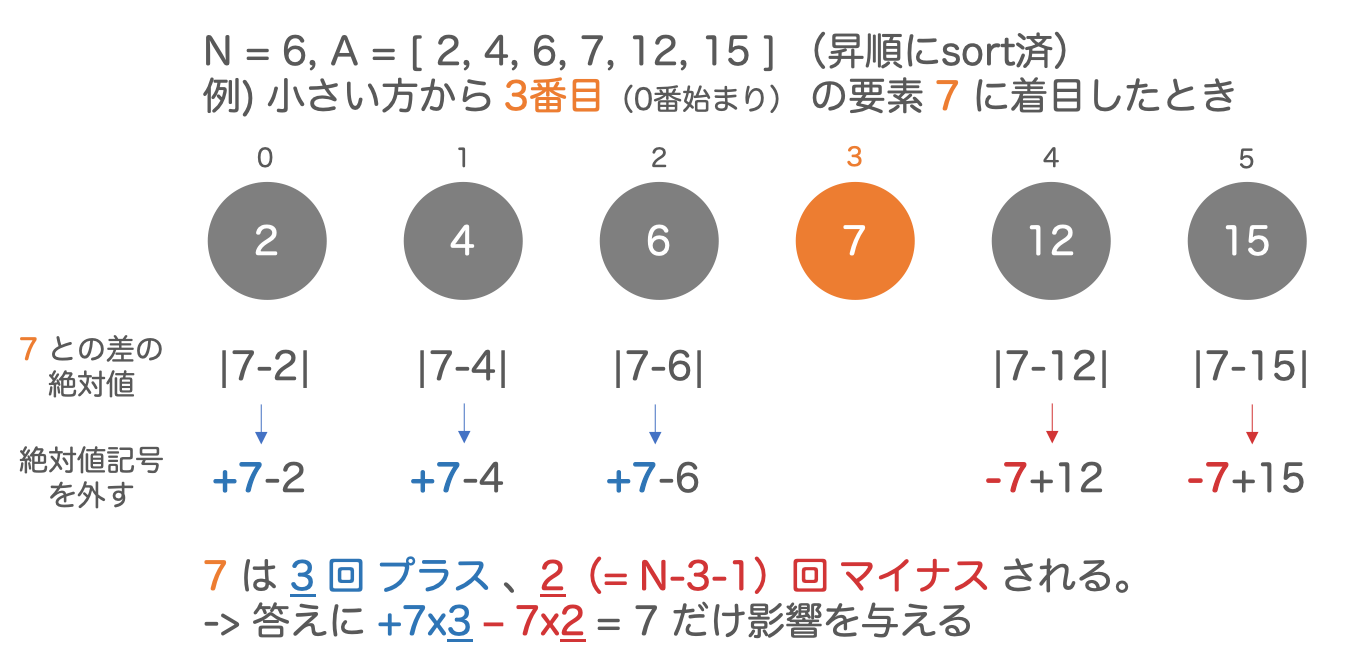
全ての要素に対してこの計算を行い、その和を求めることで、求めたい答え(全ペアの差の絶対値の和)を得ることが可能です。2重forループは無く、最も時間のかかる処理は sort の $O(NlogN)$ なので、十分に効率の良いプログラムです。
N = int(input())
A = list(map(int, input().split()))
A.sort() # 昇順に sort(O(NlogN))
ans = 0
for i, a in enumerate(A): # i番目の要素: a
ans += a*i # i回 プラス
ans -= a*(N-1-i) # (N-1-i)回 マイナス
print(ans)
「配列の要素を並び替えても答えが変わらないときは**sort すると見通しが良くなる**」「答えを直接計算するのではなく、各要素が答えに与える影響を調べて足し合わせる」は、競プロで非常によく見る考え方です。
**(答え その 2 はここを click!)**
どれくらいの難易度?
- ABC参加者の約6割が解ける
- D問題としては最も易しい(正解者が多い)部類
まとめ
パナコン(ABC)から6問ピックアップして紹介しました。
| 問題 | 概要 |
|---|---|
| A - Brick | プログラミングの基本の確認 |
| B - Many Oranges | 全探索 |
| B - Bishop | 引っかけ問題 |
| C - Swappable | 計算量を落とす工夫 |
| C - ORXOR | bit 全探索 |
| D - Sum of difference |
sort、累積和、計算量を落とす工夫 |
もちろん、今回紹介した問題は内容的にも難易度的にも序の口に過ぎません。グラフを利用する問題、ゲーム問題、区間を扱うデータ構造を利用する問題、数学的な問題、何これ?な問題...など、面白い問題がまだまだ大量に眠っています。(AtCoderには約4000問の過去問が存在します!)
少しでも興味を持ってくれた方へ
ありがたいことに、この数年間で 競プロを楽しむ環境が急速に整備されました。
実は自分が最初に競プロと出会ったのは2016年なのですが、そのときは数日やってすぐに飽きてしまいました。「何をすればいいか」「どの問題を解けばいいのか」がよくわからないまま進めた結果、的外れな学び方をしてしまい、全く面白さを感じなかったのです。
今は、わかりやすい入門記事も、競プロ入門に最適な書籍も、競プロ練習用の最高のツールも、何もかもが揃っています(競プロ界の先駆者たちに感謝です)。ちょっと嗜むだけの人からガッツリやり込みたい人まで、あらゆる人が競プロを楽しむための環境が整ったいまこそ、競プロを始めるのに最高のタイミングです!
競プロを楽しむためのコンテンツ
競プロ入門用記事
自分が最もお世話になった記事です。競プロ入門はこれ(と初級編)だけで完結するでしょう。自分は後者の記事内の 分野別 初中級者が解くべき過去問精選 100 問 でスタートダッシュが切れたおかげで、競プロにハマってしまいました。
動的計画法(DP)入門記事
ピンポイントかつ主観的な意見ですが、自分は動的計画法(DP)を理解してから競プロの楽しさが激増しました。基礎的なDPだけでも、早めに学んでおく価値はあると思います。( 高校数学 で一度はDPの考え方に触れてはいるはず。)
精進(練習)用サイト
AtCoder Problems
AtCoderの過去問を掲載したサイト。便利な機能も満載で、これのおかげでAtCoderを100倍楽しめると言っても過言ではありません。
コンテスト!
言わずもがな、コンテストに参加している時が一番エキサイティングな時間です。2時間があっという間に過ぎ去ります。AC した瞬間の喜びも、WA/TLE した時の絶望感も倍増です。
普段は忙しくて時間がとれない方も、とりあえずコンテストに出てみるだけで十分に楽しめるはずです。
FAQ
競プロって役に立つの? / 業務ではこんなの書かない
大前提として、競プロ(AtCoder)は娯楽・競技であり、「楽しいと思えるからやる」ものです。その楽しむ過程で、基本的アルゴリズムの習得や実装力の向上など、エンジニアとしての基礎体力が部分的に鍛えられます。
数学の知識が必要?
ソフトウェア関係ではない先輩に競プロの問題を見せたところ、「大学の数学みたいだね...」と言われました。確かに、特にAtCoderでは数学的な問題が多いですが、高校数学の基礎的な知識があれば十分に楽しめます。むしろ、高校までの数学を学び直す良い機会かもしれません。高校数学を超えた内容が出題されることもありますが、遭遇するたびに学習すれば問題ありません。
興味あるけど、時間がない...
競プロはちょっとしたスキマ時間でも楽しむことができます!
今回の問題を見てもわかる通り、(特にAtCoderでは)競技 "プログラミング" とはいえ "効率的なアルゴリズムを考える" パートに比重が置かれています。気になる問題をメモや頭に入れておいて休憩時間や通勤通学時間に考える だけも十分に楽しめます。(それで解法を思いついたときは、早く家に帰って実装したくてたまらなくなります。)
(番外編)AHC のススメ
AtCoderを楽しむ一番のハードルは、コンテスト参加のために週末夜にまとまった時間を確保することでしょう。自分の場合、「今日も21時から...、(競プロ)します...。」と報告するたびに妻が悲しそうな顔をするので、申し訳なく思ってしまいます。小さなお子さんがいる家庭では特に、約2時間をぶっ通しで確保するのは難しそうです。
そんな人たちにもオススメしたいのが AtCoder Heuristic Contest(AHC)です!
AtCoderにて新たに定期的に開催されるプログラミングコンテストです。ABC/ARC/AGCなどのアルゴリズムコンテストと異なり、最適解を出すのが難しい問題に対し、出来るだけ良い解を作成するコンテストとなります。
例えば この問題。 出来る限り条件を満たすように長方形を配置する問題ですが、全ての配置方法を全探索することは当然不可能です。限られた実行時間の中で出来る限り良い解を求める方法を考えて実装し、そのスコアで競うのがAHCです。Kaggleなどのコンペに近いイメージでしょうか。
一見、重くて大変そうな感じがしますが、気軽に始められます!
空き時間に少しずつ進められる
AHCは短期コンテスト(4時間ほど)と長期コンテスト(10日間ほど)の2種類があります。短期コンテストは時間確保が少し難しいですが、長期コンテストは自分のあいてる時間に少しずつ進めることが可能 です。ちょっとだけ...ちょっとだけ...と進めるうちに、 沼にハマってしまわないように気をつけましょう! (公式の注意喚起)
1つの問題であらゆるレベルの人が楽しめる
高得点を取るのは時間がかかりますが、正しい(1点以上取れる)答えを出すだけならとても簡単 です。
例えば先ほどの問題は、すべての長方形を希望の位置に大きさ1で配置するだけで、最低限の点数を確保することができます。これも正真正銘の AC です。そこから、適当に長方形を選んで他の長方形と被らないようにちょっとずつ大きさを変えていけば、スコアが伸びます。それができたら次は...、と、自分のできる範囲で徐々にスコアを伸ばしていくことができます。
ABCを含むアルゴリズムコンテストは、必要な知識がなく解けないことが多々あります。AHCでは、正の得点をとるだけであれば必要な知識はほとんどありません。それどころか(適切な戦略や評価関数などを考えることで)「その時その時で最適な行動を選択する」だけの貪欲法でも十分に点数を伸ばせます。
アルゴリズムコンテストはちょっと...という方も、ぜひ一度参加してみてください!
おわりに
コロナ禍のおうち時間でなんとなく競プロを始めて1年半がたった今、本当に良い趣味ができて良かったと感じています。この記事が、一人でも多くの人が競プロに興味を持つきっかけになれば幸いです。
