Outline
- 多目的ベイズ最適化
- MOTPE(多目的TPE)のアルゴリズム
イントロ
Optuna関連2本目です。
今回は多目的最適化のための手法・MOTPE(多目的TPE)を扱います。
TPEの多目的最適化向け拡張であるMOTPEは、2020年に論文が出たばかりの最新手法です。早速Optunaに実装され、直近のOptuna Meetup #1でも取り上げられるそうです。(参加枠逃したので誰か概要教えて…)
論文はこちら
本記事では以下の順でMOTPEの理解を試みます。
- 多目的ベイズ最適化
- 目的変数が複数存在する場合における、目的変数間の支配関係
- パレートフロント
- 獲得関数EHVI
- MOTPEのアルゴリズム
- 目的変数が複数の場合におけるデータの分割法
- EHVIの計算法
なお前記事ほど実装を細かく追うことはしません。大枠はTPESamplerと似ているので、前記事があれば不要と考えています。
1. 多目的ベイズ最適化
多目的ベイズ最適化に関しては、すでにQiitaに良い解説記事があります。
特に導入が丁寧なので、本記事がわかりにくい場合は参照してください。
1.1. 目的変数空間上の支配関係
目的変数が一つであれば、その大小から結果を比較できます。しかし目的変数が複数になると、一つが優れていても他はそうでもない、といったことがあり得るため、結果を比較する基準を決める必要があります。多目的最適化では、その基準として支配関係を考えます。
目的変数からなる空間Y上の2点 $\boldsymbol{y} = (y_1, ..., y_k)^T, \boldsymbol{y'} = (y_1, ..., y_k)^T$ について
$$\boldsymbol{y} \succeq \boldsymbol{y'} \Leftrightarrow \forall i, y_i \leq y^{'}_{i}$$
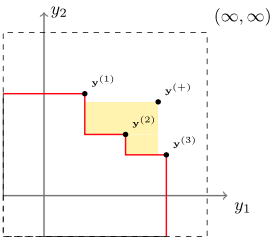
すなわち全ての目的変数で$\boldsymbol{y}$が$\boldsymbol{y'}$以下(最小化問題の場合)となっているとき、$\boldsymbol{y}$は$\boldsymbol{y'}$を支配している、と言います。例えば下図では、$\mathbf{y^{(2)}} $が$\mathbf{y}^{(+)}$を支配していますが、$\mathbf{y^{(1)}}, \mathbf{y^{(3)}}$ は$\mathbf{y}^{(+)}$を支配していません。
出典:Efficient computation of expected hypervolume improvement using box decomposition algorithms
支配関係にはバリエーションがあり、等号を含まない
$$\boldsymbol{y} \succ \boldsymbol{y'} \Leftrightarrow \forall i, y_i \leq y'_{i} \ \rm{and} \ \boldsymbol{y} \neq \boldsymbol{y'} $$
や、集合に対する支配関係
$$\boldsymbol{y} \succeq Y \Leftrightarrow \exists \boldsymbol{y'} \in Y, \boldsymbol{y} \succeq \boldsymbol{y'} $$
もあります。これらはMOTPEでデータの分割を定義する際に登場します。
また支配関係がない場合をを比較不可能と呼び、$\boldsymbol{y} \parallel \boldsymbol{y'}$ , $\boldsymbol{y} \parallel Y $などと表記します。
1.2. パレートフロント
この支配関係から、多目的最適化の目標が定まります。
目的変数空間上で$\boldsymbol{y}$が他どの点にも支配されないとき、$\boldsymbol{y}$はパレート最適解であると言います。しかし目的変数が複数ある場合、全ての変数で上回る点が他に無ければパレート最適解となるので、一般にパレート最適解は一つではありません。
多目的最適化では、複数あるパレート最適解の間での優劣は考えず、パレート最適解全ての集合を得ることを目的とします。この集合をパレート(最適)解集合とよび、パレート解集合をプロットしたときに現れる曲面をパレートフロントと呼びます。MOTPEをはじめとする多目的ベイズ最適化では、パレートフロント付近の点を多く取得することを目指します。
1.3. EHVI(Expected Hypervolume Improvement)
パレートフロントの取得を目指す上で、各時点での状況をどう評価すべきでしょうか?その基準の一つがパレート超体積です。
現状のデータセットを$\{ ( \boldsymbol{x}^{(i)}, \boldsymbol{y}^{(i)} )\}_{i=1}^N$とします。
ただし$\boldsymbol{x}^{(i)}$は入力変数(機械学習モデルのチューニングならハイパーパラメータ)、$\boldsymbol{y}^{(i)}$は目的変数(チューニングなら予測精度)を意味します。
$\{(\boldsymbol{x}^{(i)}, \boldsymbol{y}^{(i)})\}_{i=1}^N$ の中でのパレートフロントは、データを追加する度に移動していきます。この移動を評価するために参照点を決めておくと、参照点$\boldsymbol{r}$とパレート解集合$Y^* $で直方体が定義できます。
$$\cup_{\boldsymbol{y} \in Y^*}[y_1, r_1]\times ... \times [y_k, r_k]$$
上記の直方体は、パレート界集合$Y^*$に支配され、かつ参照点$\boldsymbol{r}$を支配する点の集合としても定義できます。
この直方体の超体積をパレート超体積と呼びます。
$$I_H(Y^* ) = \lambda \left(\cup_{\boldsymbol{y} \in Y^*}[y_1, r_1]\times ... \times [y_k, r_k] \right)$$
定義において$\lambda$はルベーグ測度とされますが、通常の超体積を用いることがほとんどです。
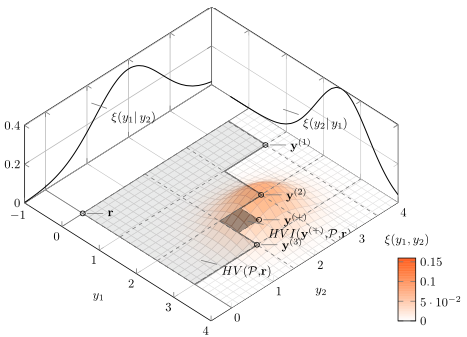
下図には、パレート界集合$Y^* = { \mathbf{y^{(i)}} }$と参照点$\boldsymbol{r}$によるパレート超体積が薄い灰色で示されています。
出典:Efficient computation of expected hypervolume improvement using box decomposition algorithms
パレート超体積はデータ追加に対して単調増加します。上図では、新たな観測$(\boldsymbol{x^+}, \boldsymbol{y^+})$による超体積増加分を濃い灰色で示しています。
この増加から、多目的最適化用の獲得関数EHVI(Expected Hypervolume Improvement)を定義できます。
$${\rm{EHVI}}_{Y^* } (\boldsymbol{x^+}) = \int{\left(I_H(Y^* \cup \{\boldsymbol{y^+}\}) - I_H(Y^*) \right) p(\boldsymbol{y^+}|\boldsymbol{x^+}) d\boldsymbol{y^+}}$$
これは新たな観測$(\boldsymbol{x^+}, \boldsymbol{y^+})$を得る前後における、パレート超体積の増分の期待値です。
通常$p(\boldsymbol{y^+}|\boldsymbol{x^+})$はガウス過程などで推定します。上の図ではオレンジで示した分布が、ガウス過程による$p(\boldsymbol{y^+}|\boldsymbol{x^+})$を示しています。この分布に従う$\boldsymbol{y^+}$によって超体積は変動するため、その期待値によってパレートフロントの前進を評価します。
2. MOTPE(多目的TPE)
MOTPEを通常のTPEと比較すると、大きな違いが2つあります。
- データの分割法
- 獲得関数の計算法
1に関しては、通常のTPEが目的変数の値によってデータを分割していたため、目的変数が複数となり単純比較ができない場合には支配関係に基づく分割に変更する必要があります。ただしこの分割は、通常TPEほど容易ではありません。
2も同様で、通常のTPEが用いていたEI(Expected Improvement)は目的関数値がどれほど増加するかについての期待値であったため、多目的最適化には適用できません。そのため獲得関数をEHVIに置き換え、TPEにより算出可能な形に変形する必要があります。幸い、EHVIの値は通常TPEにおけるEIとほぼ同じ形で計算できます。
2.1. データの分割
TPEでは、現状のデータセット$\{( \boldsymbol{x}^{(i)}, \boldsymbol{y}^{(i)})\}_{i=1}^N$を目的変数$\boldsymbol{y}$の値で上位群/下位群に分割し、双方について入力変数$\boldsymbol{x}$の分布を推定していました。しかしこの分割法は、目的変数が複数の場合には適用できません。そこで目的変数空間上における支配関係による分割を行います。
まずTPEと同様に、入力変数$\boldsymbol{x}$の各次元に独立性を仮定します。すなわち、$p(\boldsymbol{x}|\boldsymbol{y})$のカーネル密度推定においても$x$の各次元を別々に推定することができ、以降の議論では$x$を1次元変数と扱うことができます。
その上で、1次元変数$x$の分布を次のように分割します。ただし$Y^*$は目的変数上の集合であり、分割の閾値に相当します。
- 上位群:$\boldsymbol{y} \succeq Y^* $ or $\boldsymbol{y} \parallel Y^* $
集合$Y^* $を支配する点 + $Y^* $と比較不可能な点 - 下位群:$Y^* \succeq \boldsymbol{y}$
集合$Y^*$に支配される点
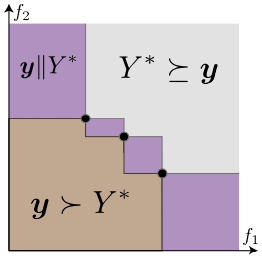
出典:Multiobjective Tree-structured Parzen Estimator for Computationally Expensive Optimization Problems
ここで集合$Y^* $は、分割の比率が
$$\gamma = p(\boldsymbol{y} \succeq Y^* \ {\rm{or}} \ \boldsymbol{y} \parallel Y^* )$$
となるように設定します。この比率$\gamma$は、ベイズルールを用いて獲得関数EHVIの式を変形する際に役立ちます。
こうして分割された上位群/下位群それぞれについて、カーネル密度推定(KDE)を用いて分布$p(x|\boldsymbol{y})$を推定します。
p(x|\boldsymbol{y}) = \left\{
\begin{array}{ll}
l(x) & ( \boldsymbol{y} \succeq Y^* \ {\rm{or}} \ \boldsymbol{y} \parallel Y^* ) \\
g(x) & (Y^* \succeq \boldsymbol{y})
\end{array}
\right.
2.2. 獲得関数(EHVI)の計算法
こうして求めた$p(x|\boldsymbol{y})$を用いて、獲得関数の計算を行います。この部分はほぼTPEにおけるEIの式変形と同様です。
EHVIの定義式は以下の通りでした。
$${\rm{EHVI}}_{Y^* }(\boldsymbol{x}) = \int{\left(I_H(Y^* \cup \{\boldsymbol{y}\}) - I_H(Y^*) \right) p(\boldsymbol{y}|\boldsymbol{x}) d\boldsymbol{y}}$$
ベイズルール $p(\boldsymbol{y}|\boldsymbol{x}) = \frac{p(\boldsymbol{x}|\boldsymbol{y}) p(\boldsymbol{y})}{p(\boldsymbol{x})}$ および条件付き期待値の定義より、
$${\rm{EHVI}}(\boldsymbol{x}) = \frac{\int{\left(I_H(Y^* \cup \{\boldsymbol{y}\}) - I_H(Y^* ) \right) p(\boldsymbol{x}|\boldsymbol{y}) p(\boldsymbol{y}) d\boldsymbol{y}}}{p(\boldsymbol{x})}$$
と変形できます。
$\left(I_H(Y^* \cup {\boldsymbol{y}}) - I_H(Y^* ) \right)$は、$\boldsymbol{y}$によってパレート超体積が増加する場合限り非ゼロとなります。したがってEHVIの分子部分の計算では、$\boldsymbol{y}$が $Y^* $ を支配する場合のみを考えれば良いことになります($\because$パレート超体積は$Y^* $に支配され、かつ参照点$\boldsymbol{r}$を支配する点の超体積でした)。
$\boldsymbol{y} \succeq Y^* $ のとき、$p(x|\boldsymbol{y})=l(x)$であったことから、変形したEHVIの分子は
\int{\left(I_H(Y^* \cup \{\boldsymbol{y}\}) - I_H(Y^* ) \right) p(\boldsymbol{x}|\boldsymbol{y}) p(\boldsymbol{y}) d\boldsymbol{y}} \\
= l(x) \int{\left(I_H(Y^* \cup \{\boldsymbol{y}\}) - I_H(Y^* ) \right) p(\boldsymbol{y}) d\boldsymbol{y}}
となります。
上式の積分部分は$x$によらない定数であることから$C$とおいて、
$$EHVI(x) = \frac{l(x)C}{p(x)}.$$
$p(x)$は単純に$p(x|\boldsymbol{y})$を積算して
$$p(x) = \gamma l(x) + (1-\gamma) g(x)$$
となる($\because$ $\gamma$の定義)ので、最終的なEHVIは
\begin{align}
{\rm{EHVI}}(x) &= \frac{l(x)C}{\gamma l(x) + (1-\gamma) g(x)} \\
&\propto \left( \gamma + (1-\gamma)\frac{g(x)}{l(x)} \right)^{-1}.
\end{align}
これはTPEにおけるEIと同じ形です。したがってTPEと同じく、$l(x) / g(x)$を最大化するような$x$を見つければ良いということになります。
終わりに
TPEに続き、MOTPEの処理を一通り追ってみました。
ご質問やご指摘などありましたらコメント頂ければ幸いです。