K Shortest Path Problem (KSP) とは, K番目(ある文脈では1~K番目)に短いパスを見つける問題です。 多重有向グラフについて始点と終点を固定した上でK shortest path problelmを解く方法として Eppsteinの アルゴリズムを実装しました[1]。
キーポイントについては, 以下のブログに簡潔にまとめられているため, こちらを参考にしてください。
Finding the k Shortest Paths (SICOMP'98) [2]
計算量についてまとめると, グラフ$G$のノード数を$n$, エッジ数を$m$とすると,
Path Graph $P$の作成に$O(m+n\log n)$
それを用いて第1~K最短路を導出するのに$O(K)$, すなわち全体で$O(m+n\log n + K)$となります。
Yenのアルゴリム[3]では$O(Kn(m+n\log n))$なので, これと比較すると大幅に計算長が削減されていることが分かります。
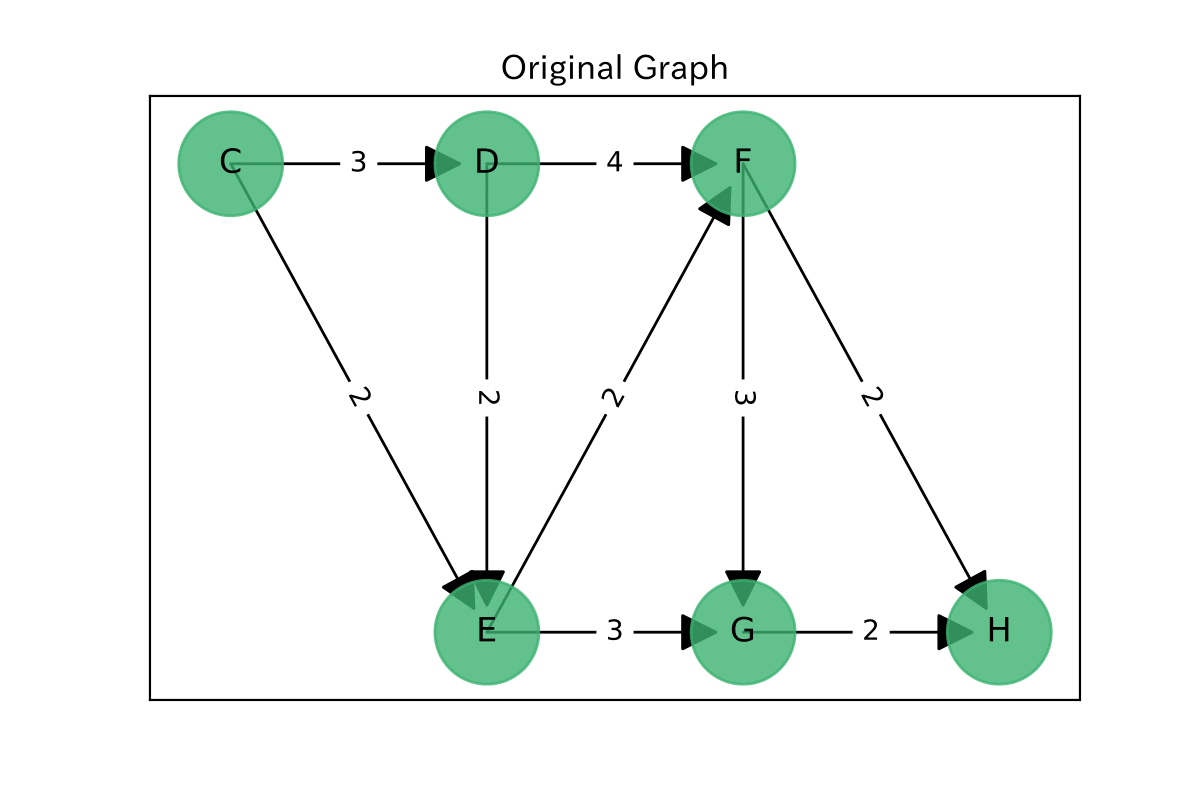
以下のグラフ$G$で, アルゴリズムの流れをざっと見ていきたいと思います。
source(始点)はCで, target(終点)はHです。
ちなみに, このグラフはYenのalgorithmの英語版Wiki[4]から引っ張ってきたものです。
心の声1
sourceとtarget固定のK Shortest Path Problem(s-t KSP)を解くのは難しいが,
target非固定で、かつ枝の重みが全て正のグラフでのK Shortest Path Proble(s-? KSP)は, 単純な最良幅優先探索で解くことができる。
元の(s-t KSP)を, パスをノードとしたグラフを作って(s-? KSP)を解く問題に帰着できないだろうか?
枝のポテンシャルの計算
最短路木の作成
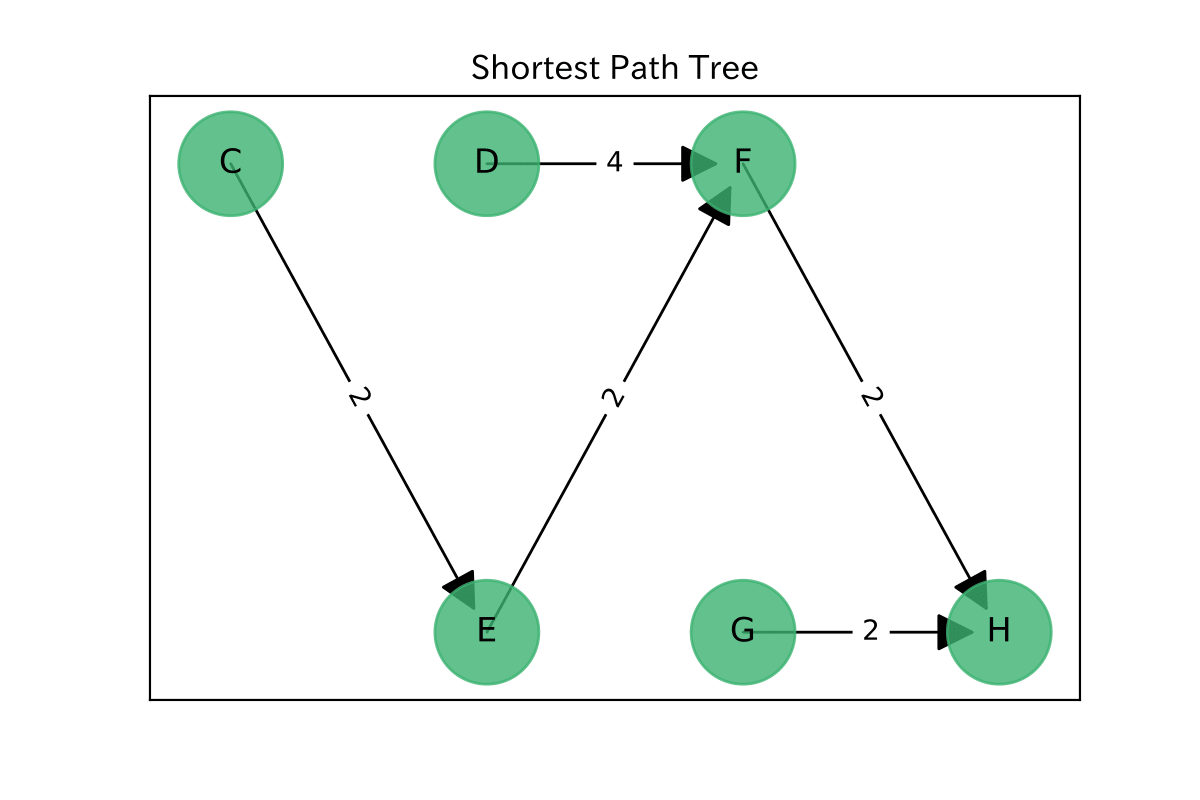
終点固定の最短路木$T$を作成します。
pred, distance = nx.dijkstra_predecessor_and_distance(G.reverse(), source=target)
T = G.edge_subgraph((i, pred[i][0]) for i in pred if pred[i])
枝のポテンシャルの計算
枝$e$のポテンシャル$\delta\left(e\right)$を
$\delta\left(e\right) := l\left(e\right) + d\left(head\left(e\right), target\right) - d\left(tail\left(e\right), target\right)$
と定めます。$l(e)$は枝$e$の長さ, $head(e)$, $tail(e)$は枝$e$の終点, 始点, $d(u, v)$ はノード$u$から$v$への最短距離です。$d(u, target)$は先に求めた最短路技から簡単に計算できます。
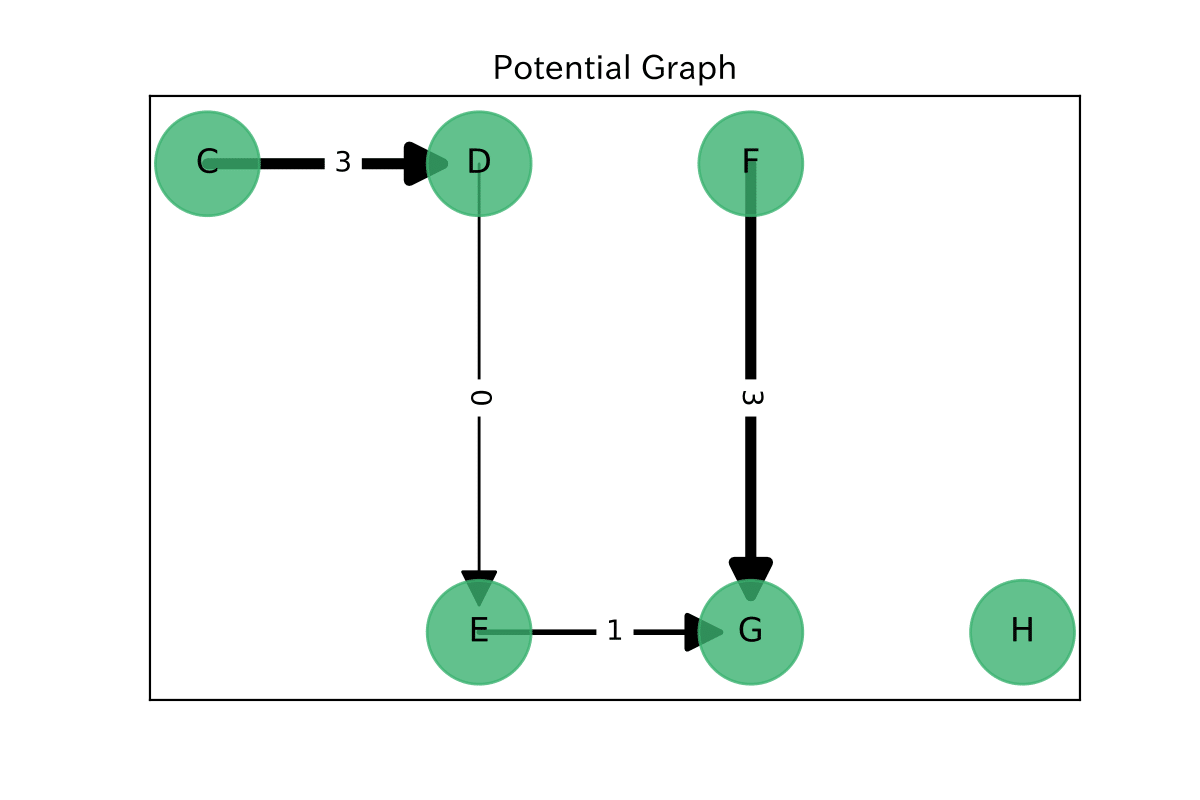
このポテンシャルは枝$e$を通ると, どれだけ最短距離から遠ざかるかを表すものであり、実際最短路木に含まれる枝に関してはこの値は$0$です。
これは, $G-T$の枝で構成されるPotential Graphです。枝の重みは先ほど定義したポテンシャル値になっています。
心の声2
グラフ上のパス$p$から$G-T$の枝の順序つき部分集合への単射が存在する($sidetrack(p)$)。
パス上でsourceから通る順に順序をつける
さらに, $sidetrack(p)$の最後尾の枝$lastsidetrack(p)$を取り除いたものを$prefix(sidetrack(p))$とすると, これもグラフ上のパスに対応しており, さらに元のパスよりも必ず短い(広義)。つまり, $prefix(sidetrack(p))$を親, $sidetrack(p)$を子として, パス長についてヒープ木[5]を作成すれば, (s-? KSP)に落とし込める!!
そこで, $sidetrack$はどのように構成すれば良いだろうか?
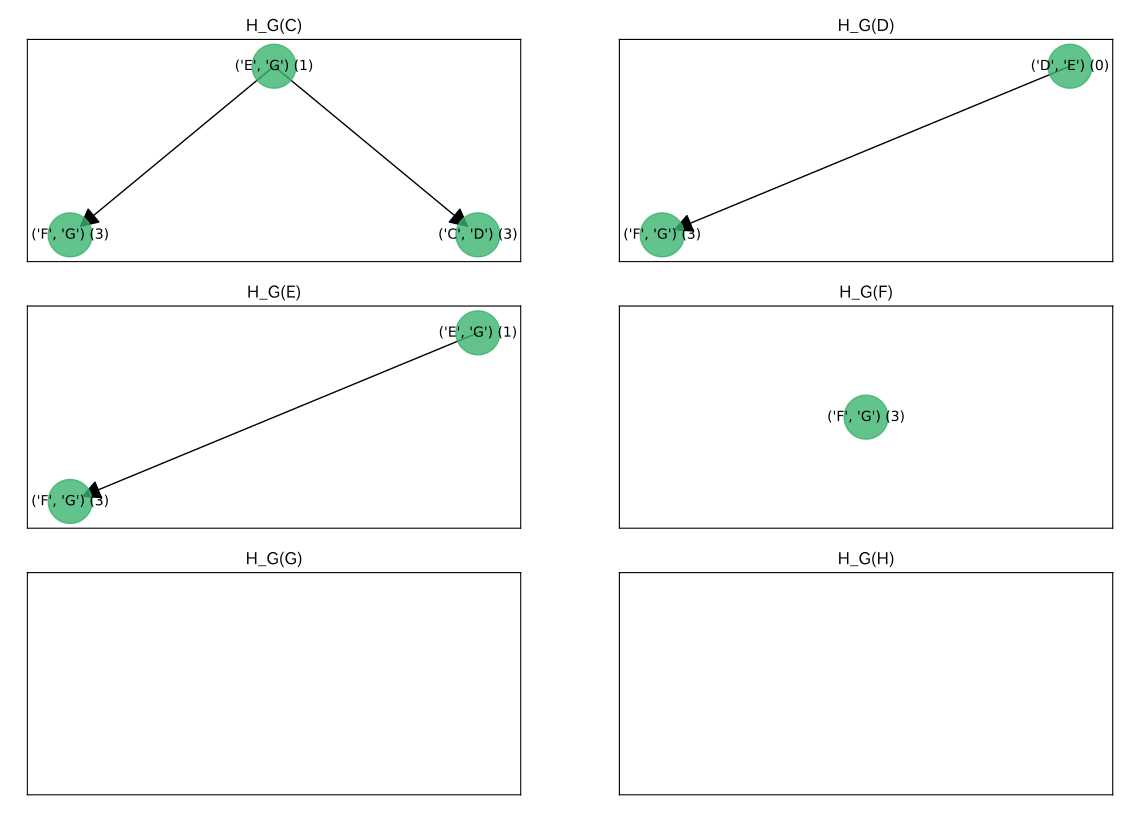
$H_G$の作成
$H_G(v)$とはノード$v$から最短路木$T$の枝のみを使って辿り着くことができる$G-T$の枝を節として, そのポテンシャル値でヒープ木にしたものです。
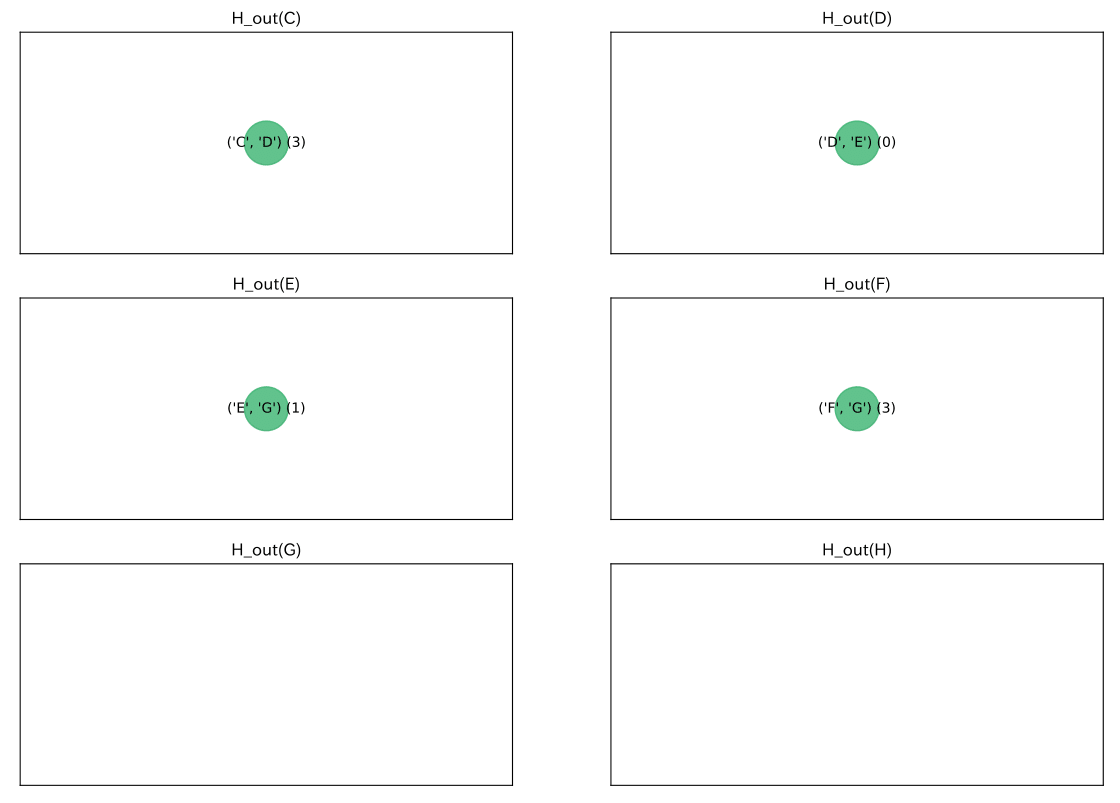
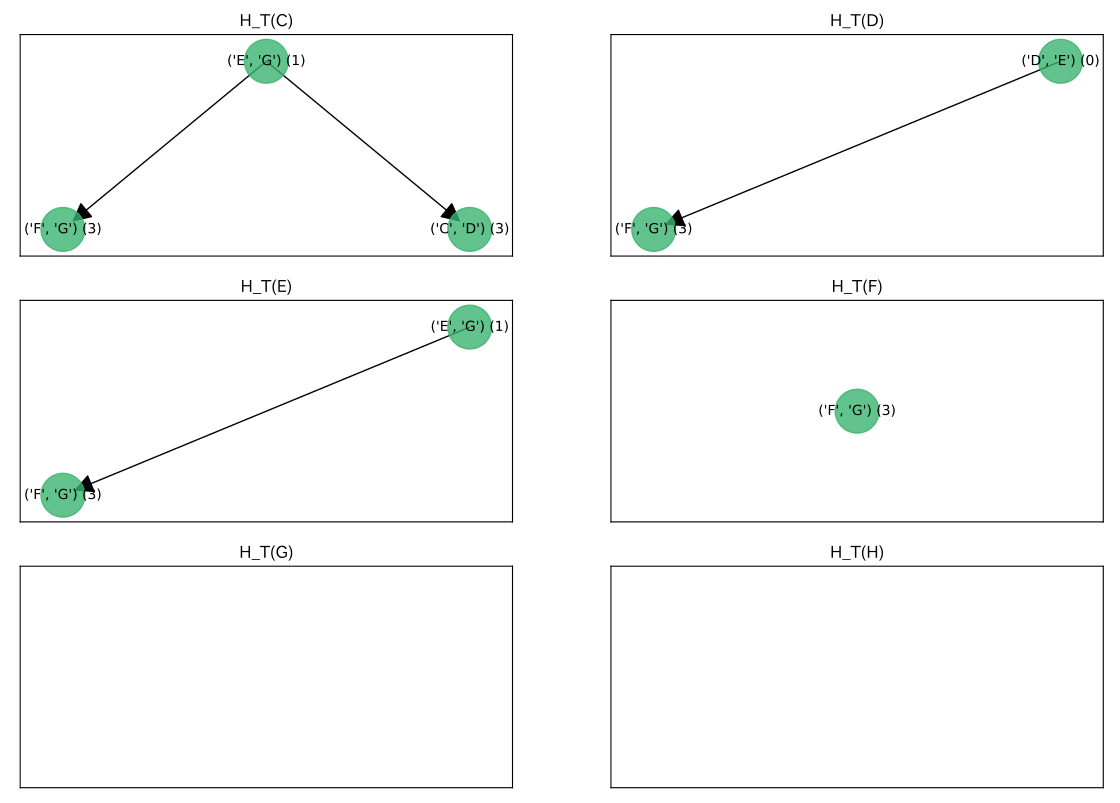
この$H_G$を効率よく作成するために, $H_{out} \rightarrow H_T \rightarrow H_G$ の順に各ノードについてヒープ木を作成していきます。 $H_{out}, H_T$の定義については, ここでは省きます。(論文[1]を参考にしてください)
後ろのソースコードでは, プログラムの簡潔化のため, 若干論文の$H_G$作成方法を変えていますが、第k最短路導出には問題ありません。
$H_{out}$
$H_T$
ヒープ木を管理するheap_tree.pyを作成しました。 2分ヒープ木は配列によって管理できますが、今回は木構造として管理しています。(なので、新しい点の挿入時におけるリンクの張り替えがめんどうでした笑
実は第k最短路を導出するだけであれば、$H_{out}$, $H_T$共に, 1分ヒープ木で十分です。
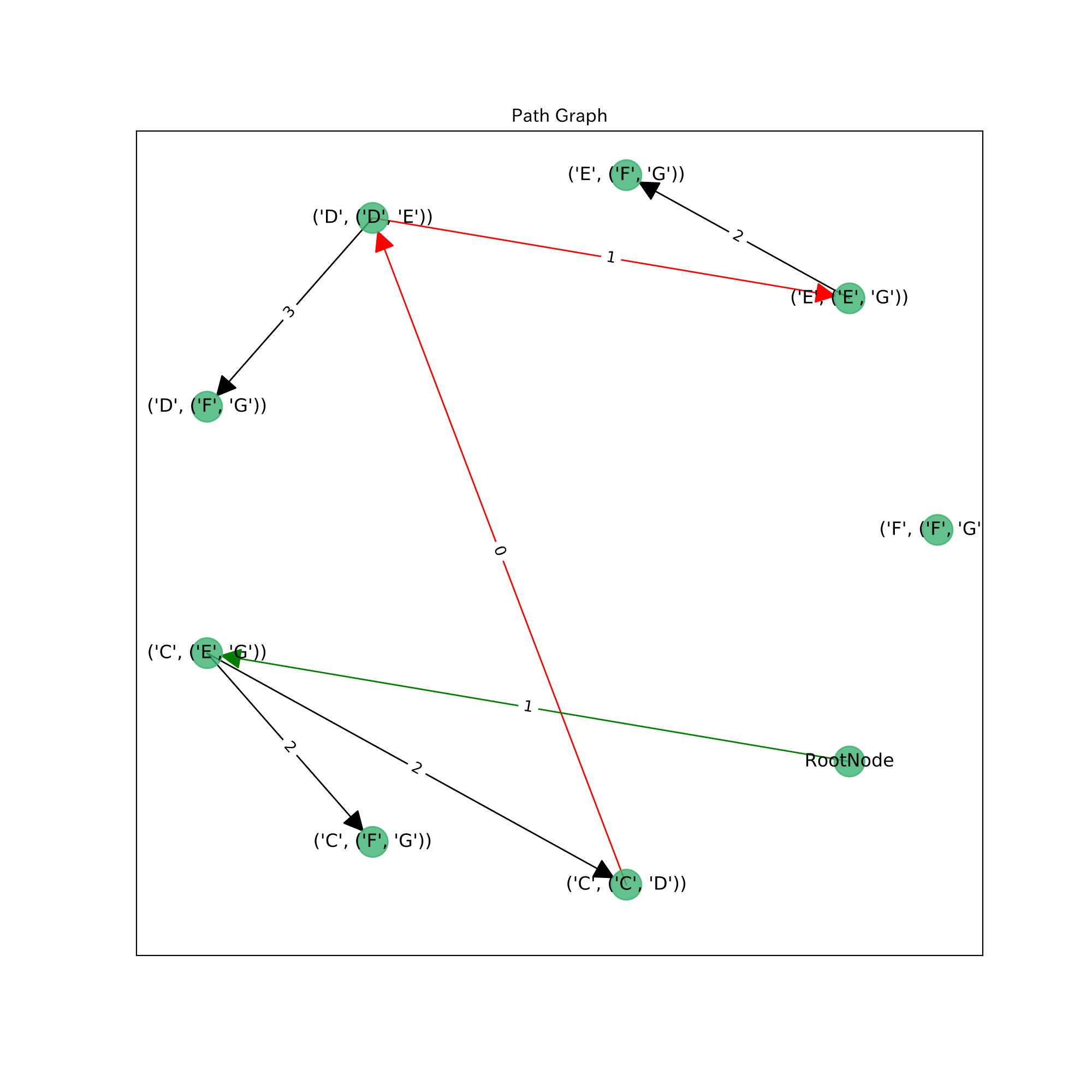
Path Graph $P$の作成
$H_G(v)$をまとめてグラフ$P$とします($P$はこの時点では非連結な森です)。
ヒープ木$H_G$の枝の重みは, 子のポテンシャル値 - 親のポテンシャル値とします。(heap edge)
また, $G-T$の枝を通ったときにどのノードに行くのかを表す枝を追加します。重みは通る枝のポテンシャル値。(cross edge)(図中: 赤色)
そしてノード$RootNode$を追加して, $H_G(source)$の根$h(source)$に枝を張り(重みは$\delta(h(source))$(図中: 緑色) $P$は完成です。
$RootNode$からのパスが元グラフ$G$でのあるパスに相当します。Path Graph $P$において, 再終点と cross edge を通ることが$G-T$のある一辺(cross edgeの始点)を通ることを表します。
あとは, この$RootNode$からtop_kをとるだけです(幅優先探索で $O(k \log k)$)。
Frederickson のアルゴリズムを用いれば $O(k)$でいけるそうですが, 今回は実装していません。
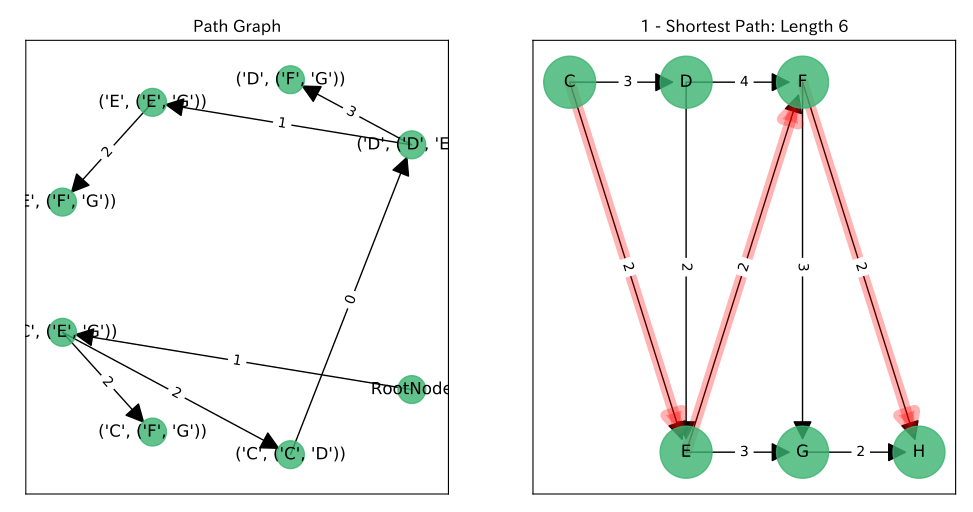
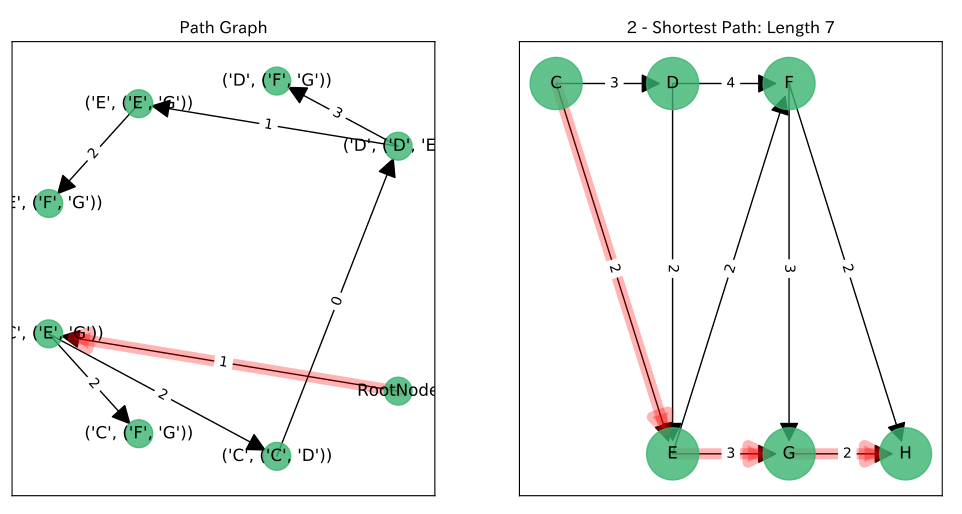
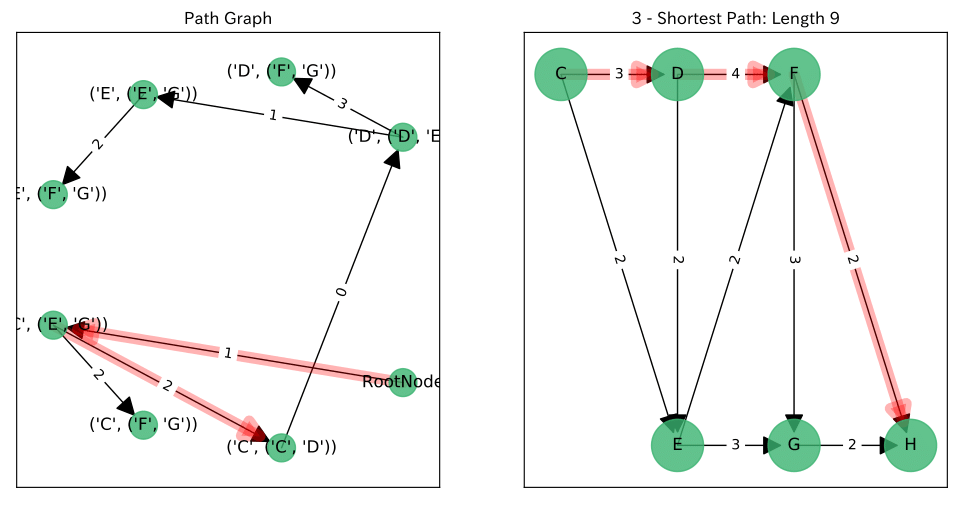
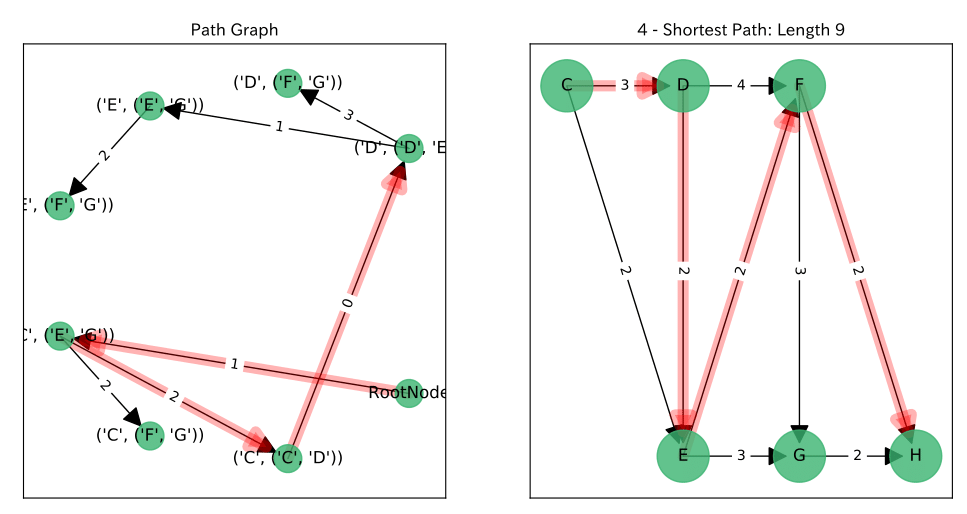
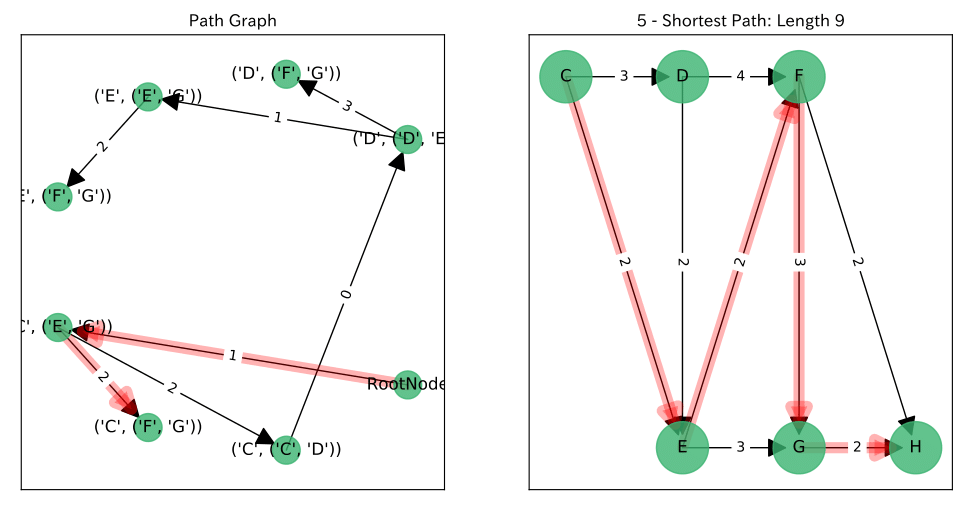
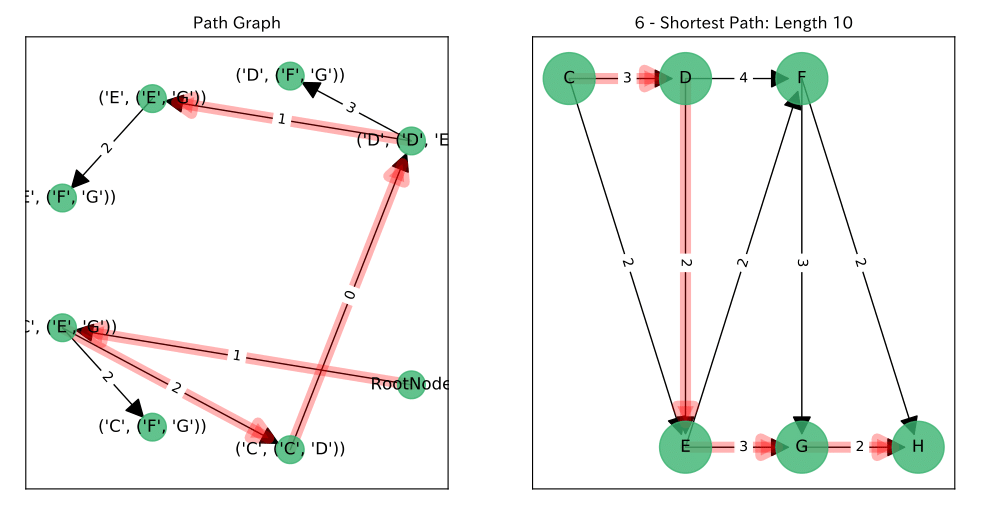
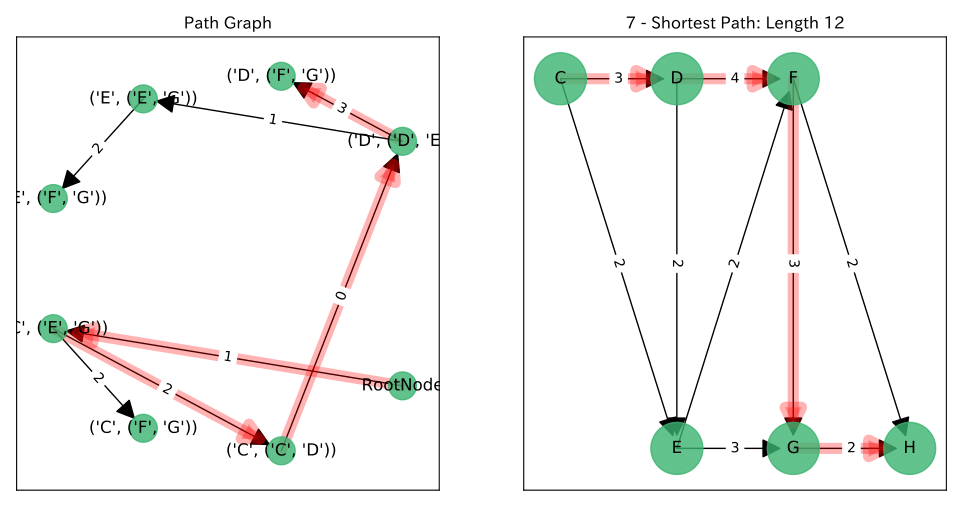
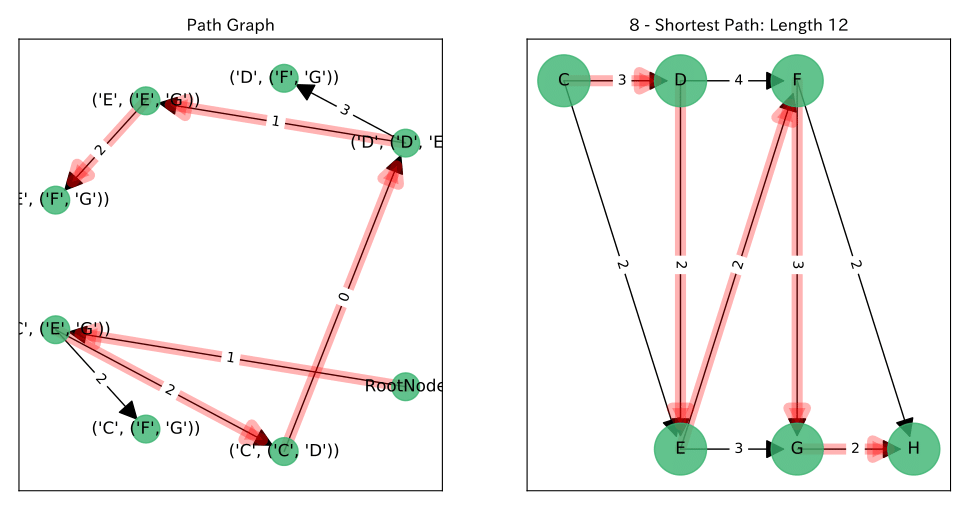
結果
左図が$P$上の$RootNode$からのパス, 右図がそれに対応する$G$上のパスです。
参考文献
[1] Eppstein, David. "Finding the k shortest paths." SIAM Journal on computing 28.2 (1998): 652-673.
[2] Finding the k Shortest Paths (SICOMP'98), http://iwiwi.hatenadiary.jp/entry/2013/12/26/001253
[3] 図解: Yen's algorithm (Find the K shortest paths), https://qiita.com/nariaki3551/items/821dc6ffdc552d3d5f22
[4] Yen's algorithm, https://en.wikipedia.org/wiki/Yen%27s_algorithm
[5] 二分木 (binary tree) とヒープ (heap), http://www.geocities.jp/m_hiroi/light/pyalgo03.html