This article presents how the memory hierarchy of a GPU can be utilized for accelerating the convolution operations represented by the following equation:
h\left(x,y\right)=\sum_{\alpha=-S}^S \sum_{\beta=-S}^S f\left(x+\alpha,y+\beta\right)g\left(\alpha,\beta\right), \,x=0,\dots,W-1, \,y=0,\dots,H-1\tag{1}
where, $f\left(x,y\right)$ is an image with pixel coordinates $\left(x, y\right)$ in the coordinate system shown on the left in Fig.1, $W$ and $H$ are the width and height of the image, $g\left(\alpha,\beta\right)$ is a filter with the coordinate system shown on the right in Fig.1, and $S$ determines the size of the filter as $\left(2S+1\right)\times\left(2S+1\right)$.
*Figure 1. A coordinate system of an image and a filter.*
If you are not familiar with convolution and CUDA, the fundamentals of them can be seen in the part 1 of this article: https://qiita.com/naoyuki_ichimura/items/8c80e67a10d99c2fb53c.
If you would like to directory access the example code used in this article, see https://github.com/NaoyukiIchimura/cuda_image_filtering_constant and https://github.com/NaoyukiIchimura/cuda_image_filtering_shared.
1. The memory hierarchy of a GPU
Two types of memory are equipped on a GPU. The first type is on-board memory. Global memory used in the part 1 of this article is this type. The second type is on-chip memory that is associated with each MP (Multi-Processor). The prominent feature of on-chip memory is its latency; the latency of on-chip memory is much shorter than the one of on-board memory. Thus data reuse utilizing on-chip memory is a key to improve the efficiency of GPU computing. In the strategy of data reuse, data read many times are stored in memory with short latency and reusing them for fast computation.
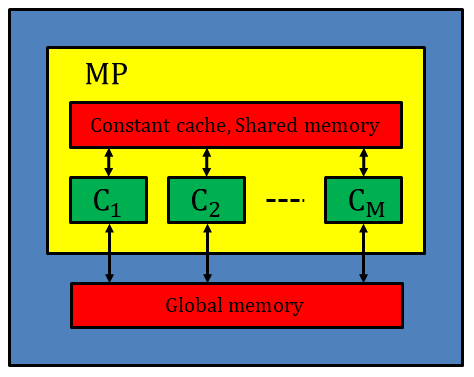*Figure 2. The overview of the memory hierarchy of a GPU. On-board memory such as global memory and on-chip memory such as constant cache and shared memory are equipped. The major differences between on-board and on-chip memory are their latency and capacity; on-chip memory latency is much shorter, but its capacity is much smaller.*
In this article, constant cache and shared memory shown in Fig.2 are adopted to accelerate the convolution operations. First, utilizing constant cache via constant memory is presented, and then utilizing shared memory is demonstrated. The total amount of constant memory and shared memory of a GPU can be checked by the command deviceQuery as exemplified by the followings:
Device 0: "GeForce GTX 1080 Ti"
CUDA Driver Version / Runtime Version 9.2 / 9.2
CUDA Capability Major/Minor version number: 6.1
Total amount of global memory: 11178 MBytes (11721506816 bytes)
(28) Multiprocessors, (128) CUDA Cores/MP: 3584 CUDA Cores
GPU Max Clock rate: 1582 MHz (1.58 GHz)
Memory Clock rate: 5505 Mhz
Memory Bus Width: 352-bit
L2 Cache Size: 2883584 bytes
Maximum Texture Dimension Size (x,y,z) 1D=(131072), 2D=(131072, 65536), 3D=(16384, 16384, 16384)
Maximum Layered 1D Texture Size, (num) layers 1D=(32768), 2048 layers
Maximum Layered 2D Texture Size, (num) layers 2D=(32768, 32768), 2048 layers
Total amount of constant memory: 65536 bytes
Total amount of shared memory per block: 49152 bytes
Total number of registers available per block: 65536
Warp size: 32
Maximum number of threads per multiprocessor: 2048
Maximum number of threads per block: 1024
Max dimension size of a thread block (x,y,z): (1024, 1024, 64)
Max dimension size of a grid size (x,y,z): (2147483647, 65535, 65535)
Maximum memory pitch: 2147483647 bytes
Texture alignment: 512 bytes
Concurrent copy and kernel execution: Yes with 2 copy engine(s)
Run time limit on kernels: No
Integrated GPU sharing Host Memory: No
Support host page-locked memory mapping: Yes
Alignment requirement for Surfaces: Yes
Device has ECC support: Disabled
Device supports Unified Addressing (UVA): Yes
Device supports Compute Preemption: Yes
Supports Cooperative Kernel Launch: Yes
Supports MultiDevice Co-op Kernel Launch: Yes
Device PCI Domain ID / Bus ID / location ID: 0 / 21 / 0
Compute Mode:
< Default (multiple host threads can use ::cudaSetDevice() with device simultaneously) >
Figure 2. The output of the command "deviceQuery" for the GPU, GeForce GTX 1080 Ti. The information obtained by the command is important to write a program using CUDA.
2. Utilizing constant cache to reuse filter coefficients
There are two attributes of constant memory. The first attribute is that constant memory is writable and readable by host code but only readable by kernel code, which means that all threads executed by a GPU use the same data in constant memory. The second one is constant memory has own on-chip cache although it is on-board. From this specification, constant memory is suitable to reuse data that are not changed during convolution and read by all threads. Filter coefficients are exactly such data.
A constant variable has to be declared with __constant__ specifier in global scope. Since a constant memory space cannot be dynamically allocated, the size of the space should be determined beforehand. The following code is an example to declare a constant variable:
const unsigned int MAX_FILTER_SIZE = 79;
__device__ __constant__ float d_cFilterKernel[ MAX_FILTER_SIZE * MAX_FILTER_SIZE ];
where, the specifier __device__ means that the variable is used only by a kernel function. When you declare a constant variable, check out the total amount of constant memory of your GPU. It's 64KB for GeForce GTX 1080 Ti. Since the maximum filter size is 79 in the above code, the size of the variable is 79$\times$79$\times$4$\simeq$25KB for float.
Filter coefficients assigned by host code can be transferred to constant memory of a device by the function cudaMemcpyToSymbol() instead of cudaMemcpy():
unsigned int filterKernelSizeByte = filterSize * filterSize * sizeof(float);
cudaMemcpyToSymbol( d_cFilterKernel, h_filterKernel, filterKernelSizeByte, 0, cudaMemcpyHostToDevice ) );
where, the variable h_filterKernel contains filter coefficients set by a host, and filterSize represents the size of a filter.
The kernel function for the convolution operations can be written as follows:
template <typename T>
__global__ void imageFilteringKernel( const T *d_f, const unsigned int paddedW, const unsigned int paddedH,
const int S,
T *d_h, const unsigned int W, const unsigned int H )
{
// Set the padding size and filter size
unsigned int paddingSize = S;
unsigned int filterSize = 2 * S + 1;
// Set the pixel coordinate
const unsigned int j = blockIdx.x * blockDim.x + threadIdx.x + paddingSize;
const unsigned int i = blockIdx.y * blockDim.y + threadIdx.y + paddingSize;
// The multiply-add operation for the pixel coordinate ( j, i )
if( j >= paddingSize && j < paddedW - paddingSize && i >= paddingSize && i < paddedH - paddingSize ) {
unsigned int oPixelPos = ( i - paddingSize ) * W + ( j - paddingSize );
d_h[oPixelPos] = 0.0;
for( int k = -S; k <= S; k++ ) {
for( int l = -S; l <= S; l++ ) {
unsigned int iPixelPos = ( i + k ) * paddedW + ( j + l );
unsigned int coefPos = ( k + S ) * filterSize + ( l + S );
d_h[oPixelPos] += d_f[iPixelPos] * d_cFilterKernel[coefPos];
}
}
}
}
The difference between the kernel functions using constant memory and using only global memory is merely the place of filter coefficients. In order to evaluate the effectiveness of data reuse for filter coefficients, the same execution configuration, gradient filter, 1920$\times$1080 image, CPU and GPU shown in the part 1 were used. The computation times of the kernel functions are summarized in Tab. 1 and Tab. 2.
| Filter Size | CPU (Filtering) |
GPU (Filtering) |
GPU (Transfer) |
Speed-up (Filtering) |
Speed-up (Overall) |
|---|---|---|---|---|---|
| 3x3 | 19.86 | 0.18 | 4.67 | 110X | 4.1X |
| 5x5 | 46.04 | 0.39 | 4.66 | 118X | 9.1X |
| Table 1. The computation times of the kernel function utilizing constant memory to reuse the coefficients of the gradient filter. The unit is [ms]. Note that the computation times varied by trial because the non-real OS (Linux) was used. |
| Filter size | CPU (Filtering) |
GPU (Filtering) |
GPU (Transfer) |
Speed-up (Filtering) |
Speed-up (Overall) |
|---|---|---|---|---|---|
| 3x3 | 19.78 | 0.54 | 4.62 | 36.6X | 3.8X |
| 5x5 | 45.90 | 1.46 | 4.70 | 31.4X | 7.5X |
| Table 2. The computaion times of the kernel function using only global memory. The unit is [ms]. |
As we can see from the tables, reusing the filter coefficients was useful to shorten the computation time for filtering. The kernel function utilizing constant memory was about 3X faster than one using only global memory. This result demonstrates that constant cache can be utilized via constant memory for the convolution operations. The filtering results by the GPU was the same as the results by the CPU, provided the option of nvcc --fmad was false.
You can find the code used to compute the result at https://github.com/NaoyukiIchimura/cuda_image_filtering_constant.
3. Utilizing shared memory to reuse pixel data
In CUDA, an image is divided into blocks for parallel computing as shown in Fig. 3. The pixel data in a block are read many times by threads in performing the convolution operations. Thus storing the pixel data in on-chip memory and reusing them might be useful for efficient computing.
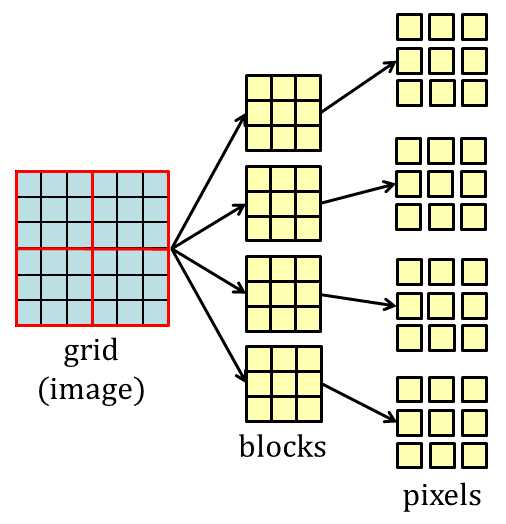*Figure 3. Blocks for parallel computing.*
Since a MP is assigned to each block in parallel computing, shared memory in a MP is used for reusing the pixel data. Storing the pixel data is carried out by the following two steps: (1) transferring an image from a host to global memory of a device, (2) copying the pixel data in a block to shared memory by threads. In the second step, we need to pay attention to the balance between the computational costs for copying the pixel data and performing the convolution operations. If the frequency in reuse of the pixel data is low, the cost of copying the pixel data might be larger than one for convolution, in which reusing the pixel data is ineffective. In general, utilizing shared memory is useful for a large size filter, because the frequency of reusing data increases.
As the first step is explained in the part1, the procedure of the second step is shown. In order to perform filtering for the pixel data in a block correctly, the pixel data surrounding a block should be copied to shared memory. For a $\left(2S+1\right)\left(2S+1\right)$ filter, we should add $S$ pixel(s) to a block as shown in Fig.4. A block with the surrounding data is called a tile here, and all the pixel data in a tile have to be copied.
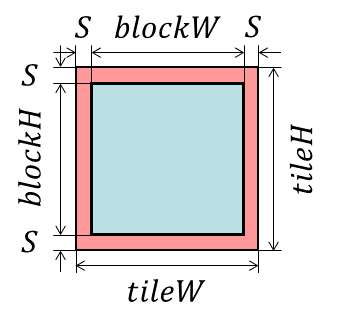*Figure 4. A tile for data reuse. The pixel data surrounding a block should be copied to shared memory with a block to perform filtering correctly. Adding $S$ pixel(s) to a block for a $\left(2S+1\right)\left(2S+1\right)$ filter makes a tile, and all the pixel data in a tile are copied to shared memory.*
The execution configuration can be set as follows:
const unsigned int tileW = blockW + 2 * S;
const unsigned int tileH = blockH + 2 * S;
const dim3 grid( iDivUp( W, blockW ), iDivUp( H, blockH ) );
const dim3 threadBlock( tileW, tileH );
where, iDivUp() is an inline function of the ceiling function for unsigned int variables:
inline unsigned int iDivUp( const unsigned int &a, const unsigned int &b ) { return ( a%b != 0 ) ? (a/b+1):(a/b); }
Note that the threads are assigned to the pixel data in a tile for both copy and convolution.
The block size:
const unsigned int blockW = 32;
const unsigned int blockH = 32;
were adopted for the kernel functions using only global memory and utilizing constant memory. However, we cannot assign threads for all the pixel data in a tile, because the number of threads tileWtileH=(blockW+2S)(blockH+2S) exceeds the maximum number of threads per block of GeForce GTX 1080 Ti, 1024, even for S=1. Although a simple way to avoid this problem is to decrease the block size, e.g., blockW = 16 and blockH = 16, it's unpractical for a large size filter such as a Gaussian filter. For example, let's assume that the Gaussian filter with the standard deviation $\sigma=3.2$ is applied, and the size of the filter is determined as $2\times\lceil4\sigma\rceil+1$, which means that the radius of the filter is almost $4\sigma$ and the size is odd number. Since the filter size is 27, the number of threads becomes (16+2$\times$13)(16+2$\times$13)=1764 because $S$=13. If we set blockW = 8 and blockH = 8, the number of threads is 1156 that is still larger than 1024. Thus it's difficult to apply the 27$\times$27 filter with data reuse. This is not acceptable because data reuse is effective for a large size filter.
In order address the problem, subblocks are introduced as shown in Fig.5. Let's assume threadBlockH = 8. Since the number of pixels in a subblock is (32+2$\times$13)$\times$8=464, we can assign threads to all the pixels in the first subblock. The convolution operations for the rest of the subblocks are performed sequentially by the threads.
*Figure 5. Subblocks on a tile. Threads are assigned to the pixel data in the first subblock, and the convolution operations for the rest of the subblocks are performed sequentially by the threads.*
The execution configuration for using subblocks is as follows:
const unsigned int blockW = 32;
const unsigned int blockH = 32;
const unsigned int tileW = blockW + 2 * hFilterSize;
const unsigned int tileH = blockH + 2 * hFilterSize;
const unsigned int threadBlockH = 8;
const dim3 grid( iDivUp( W, blockW ), iDivUp( H, blockH ) );
const dim3 threadBlock( tileW, threadBlockH );
Since a block of the pixel data and a thread block are different under this configuration, the former is referred as a data block hereafter.
The size of shared memory required to store a tile is:
const unsigned int sharedMemorySizeByte = tileW * tileH * sizeof(float);
We have to check if this size exceeds the total amount of shared memory per block. In GeForce GTX 1080 Ti, the total amount of shared memory per block is 48KB as shown in the output of the command deviceQuery. Therefore, the maximum filter size for float variables can be computed from the equation 4(32+2$S_{max}$)(32+2$S_{max}$)=49152. Since $S_{max}$=39.4, the maximum filter size is 2$\times$39+1=79 as declared with the constant memory variable.
The variables grid, threadBlock and sharedMemorySizeByte are given to the kernel function for filtering as follows:
imageFilteringKernel<<<grid,threadBlock,sharedMemorySizeByte>>>( d_f, paddedW, paddedH,
blockW, blockH, S,
d_h, W, H );
The variables for the size of a data block, blockW and blockH, have to be passed to the kernel function, because the built-in variable blockDim represents the size of a thread block.
In the kernel function, we can obtain the following values using the arguments and built-in variables. The number of subblocks in a tile is computed by:
const unsigned int tileW = blockW + 2 * S;
const unsigned int tileH = blockH + 2 * S;
const unsigned int noSubBlocks = static_cast<unsigned int>(ceil( static_cast<double>(tileH)/static_cast<double>(blockDim.y) ));
where, the built-in variable blockDim has the components blockDim.x=tileW and blockDim.y=threadBlockH. Note that the inline function iDivUp() cannot be used instead of ceil() in a kernel function. The position of a data block in a padded image is given by:
const unsigned int blockStartCol = blockIdx.x * blockW + S;
const unsigned int blockEndCol = blockStartCol + blockW;
const unsigned int blockStartRow = blockIdx.y * blockH + S;
const unsigned int blockEndRow = blockStartRow + blockH;
where, the components blockIdx.x and blockIdx.y vary within [ 0, iDivUp( W, blockW ) - 1 ] and [ 0, iDivUp( H, blockH ) - 1 ], respectively. The position of a tile in a padded image is obtained using the position of a data block as follows:
const unsigned int tileStartCol = blockStartCol - S;
const unsigned int tileEndCol = blockEndCol + S;
const unsigned int tileEndClampedCol = min( tileEndCol, paddedW );
const unsigned int tileStartRow = blockStartRow - S;
const unsigned int tileEndRow = blockEndRow + S;
const unsigned int tileEndClampedRow = min( tileEndRow, paddedH );
The declaration of the variable in shared memory is:
extern __shared__ T sData[];
where, extern is required to allocate the array dynamically in accordance with the size determined by the variable sharedMemorySizeByte in host code, the declaration specifier __shared__ means that sData points a shared memory space, and T is the type name used in the template kernel function.
Copying the pixel data in a tile to shared memory is executed by the following code:
unsigned int tilePixelPosCol = threadIdx.x;
unsigned int iPixelPosCol = tileStartCol + tilePixelPosCol;
for( unsigned int subBlockNo = 0; subBlockNo < noSubBlocks; subBlockNo++ ) {
unsigned int tilePixelPosRow = threadIdx.y + subBlockNo * blockDim.y;
unsigned int iPixelPosRow = tileStartRow + tilePixelPosRow;
if( iPixelPosCol < tileEndClampedCol && iPixelPosRow < tileEndClampedRow ) { // Check if the pixel in the image
unsigned int iPixelPos = iPixelPosRow * paddedW + iPixelPosCol;
unsigned int tilePixelPos = tilePixelPosRow * tileW + tilePixelPosCol;
sData[tilePixelPos] = d_f[iPixelPos];
}
}
__syncthreads();
where, ( tilePixelPosCol, tilePixelPosRow ) shows a pixel coordinate in a tile, ( iPixelPosCol, iPixelPosRow ) denotes a pixel coordinate in a padded image, and the components threadIdx.x and threadIdx.y vary within [ 0, tileW - 1 ] and [ 0, threadBlockH - 1 ], respectively. The loop for( unsigned int subBlockNo = 0; subBlockNo < noSubBlocks; subBlockNo++ ) is for sequential processing for subblocks. The function __syncthreads() must be called to wait until all the threads complete copying the pixel data. The data in shared memory cannot be used safely in subsequent code without calling the function.
The convolution operations are performed by the following code:
tilePixelPosCol = threadIdx.x;
iPixelPosCol = tileStartCol + tilePixelPosCol;
for( unsigned int subBlockNo = 0; subBlockNo < noSubBlocks; subBlockNo++ ) {
unsigned int tilePixelPosRow = threadIdx.y + subBlockNo * blockDim.y;
unsigned int iPixelPosRow = tileStartRow + tilePixelPosRow;
// Check if the pixel in the tile and image.
// Note that the apron of the tile is excluded.
if( iPixelPosCol >= tileStartCol + S && iPixelPosCol < tileEndClampedCol - S &&
iPixelPosRow >= tileStartRow + S && iPixelPosRow < tileEndClampedRow - S ) {
// Compute the pixel position for the output image
unsigned int oPixelPosCol = iPixelPosCol - S; // removing the origin
unsigned int oPixelPosRow = iPixelPosRow - S;
unsigned int oPixelPos = oPixelPosRow * W + oPixelPosCol;
unsigned int tilePixelPos = tilePixelPosRow * tileW + tilePixelPosCol;
d_h[oPixelPos] = 0.0;
for( int i = -S; i <= S; i++ ) {
for( int j = -S; j <= S; j++ ) {
int tilePixelPosOffset = i * tileW + j;
int coefPos = ( i + S ) * kernelSize + ( j + S );
d_h[oPixelPos] += sData[ tilePixelPos + tilePixelPosOffset ] * d_cFilterKernel[coefPos];
}
}
}
}
where, ( oPixelPosCol, oPixelPosRow ) represents a pixel coordinate in an output image with the size $W$ and $H$. Since the computational cost of this code is almost determined by the filter size, the cost for copying the pixel data to shared memory is paid off for a large size filter.
By combining the above code, we can obtain the following kernel function:
template <typename T>
__global__ void imageFilteringKernel( const T *d_f, const unsigned int paddedW, const unsigned int paddedH,
const unsigned int blockW, const unsigned int blockH, const int S,
T *d_h, const unsigned int W, const unsigned int H )
{
//
// Note that blockDim.(x,y) cannot be used instead of blockW and blockH,
// because the size of a thread block is not equal to the size of a data block
// due to the apron and the use of subblocks.
//
//
// Set the size of a tile
//
const unsigned int tileW = blockW + 2 * S;
const unsigned int tileH = blockH + 2 * S;
//
// Set the number of subblocks in a tile
//
const unsigned int noSubBlocks = static_cast<unsigned int>(ceil( static_cast<double>(tileH)/static_cast<double>(blockDim.y) ));
//
// Set the start position of a data block, which is determined by blockIdx.
// Note that since padding is applied to the input image, the origin of the block is ( S, S )
//
const unsigned int blockStartCol = blockIdx.x * blockW + S;
const unsigned int blockEndCol = blockStartCol + blockW;
const unsigned int blockStartRow = blockIdx.y * blockH + S;
const unsigned int blockEndRow = blockStartRow + blockH;
//
// Set the position of the tile which includes the data block and its apron
//
const unsigned int tileStartCol = blockStartCol - S;
const unsigned int tileEndCol = blockEndCol + S;
const unsigned int tileEndClampedCol = min( tileEndCol, paddedW );
const unsigned int tileStartRow = blockStartRow - S;
const unsigned int tileEndRow = blockEndRow + S;
const unsigned int tileEndClampedRow = min( tileEndRow, paddedH );
//
// Set the size of the filter kernel
//
const unsigned int kernelSize = 2 * S + 1;
//
// Shared memory for the tile
//
extern __shared__ T sData[];
//
// Copy the tile into shared memory
//
unsigned int tilePixelPosCol = threadIdx.x;
unsigned int iPixelPosCol = tileStartCol + tilePixelPosCol;
for( unsigned int subBlockNo = 0; subBlockNo < noSubBlocks; subBlockNo++ ) {
unsigned int tilePixelPosRow = threadIdx.y + subBlockNo * blockDim.y;
unsigned int iPixelPosRow = tileStartRow + tilePixelPosRow;
if( iPixelPosCol < tileEndClampedCol && iPixelPosRow < tileEndClampedRow ) { // Check if the pixel in the image
unsigned int iPixelPos = iPixelPosRow * paddedW + iPixelPosCol;
unsigned int tilePixelPos = tilePixelPosRow * tileW + tilePixelPosCol;
sData[tilePixelPos] = d_f[iPixelPos];
}
}
//
// Wait for all the threads for data loading
//
__syncthreads();
//
// Perform convolution
//
tilePixelPosCol = threadIdx.x;
iPixelPosCol = tileStartCol + tilePixelPosCol;
for( unsigned int subBlockNo = 0; subBlockNo < noSubBlocks; subBlockNo++ ) {
unsigned int tilePixelPosRow = threadIdx.y + subBlockNo * blockDim.y;
unsigned int iPixelPosRow = tileStartRow + tilePixelPosRow;
// Check if the pixel in the tile and image.
// Note that the apron of the tile is excluded.
if( iPixelPosCol >= tileStartCol + S && iPixelPosCol < tileEndClampedCol - S &&
iPixelPosRow >= tileStartRow + S && iPixelPosRow < tileEndClampedRow - S ) {
// Compute the pixel position for the output image
unsigned int oPixelPosCol = iPixelPosCol - S; // removing the origin
unsigned int oPixelPosRow = iPixelPosRow - S;
unsigned int oPixelPos = oPixelPosRow * W + oPixelPosCol;
unsigned int tilePixelPos = tilePixelPosRow * tileW + tilePixelPosCol;
d_h[oPixelPos] = 0.0;
for( int i = -S; i <= S; i++ ) {
for( int j = -S; j <= S; j++ ) {
int tilePixelPosOffset = i * tileW + j;
int coefPos = ( i + S ) * kernelSize + ( j + S );
d_h[oPixelPos] += sData[ tilePixelPos + tilePixelPosOffset ] * d_cFilterKernel[coefPos];
}
}
}
}
}
The evaluation of data reuse utilizing shared memory was carried out by measuring computation time for the gradient filter applied to the 1920$\times$1080 image by the CPU and CPU. The results shown in Tab.3 demonstrate that copying the pixel data in a tile to shared memory is not so effective for the 3$\times$3 filter, because the constant memory version was comparable to this version. However, it's useful for the 5$\times$5 filter and the computation time reached 0.26[ms] which was 177X faster than the CPU. This means that once you transfer an image with the size 1920$\times$1080 to the GPU, you can perform 5$\times$5 filtering 100 times in 26[ms]. I think it's not so bad especially for applying a filter bank for applications such as convolutional neural networks and scale space analysis. Of course, the filtering results by the CPU and GPU were identical.
| Filter Size | CPU (Filtering) |
GPU (Filtering) |
GPU (Transfer) |
Speed-up (Filtering) |
Speed-up (Overall) |
|---|---|---|---|---|---|
| 3x3 | 19.86 | 0.16 | 4.65 | 124X | 4.1X |
| 5x5 | 46.09 | 0.26 | 4.63 | 177X | 9.4X |
| Table 3. The computation times of the kernel function utilizing shared memory to reuse the pixel data in a tile. The unit is [ms]. |
In order to emphasize the effectiveness of data reuse utilizing shared memory, the computation times for the Gaussian filter with the standard deviation $\sigma=3.2$ were measured. The size of the filter was computed as $2\times\lceil4\sigma\rceil+1=27$. The results shown in Tab.4 demonstrate that the kernel function utilizing shared memory was about 4X and 2X faster than the other kernel functions. The filtering result by the GPU is in Fig.6.
| Version | CPU (Filtering) |
GPU (Filtering) |
GPU (Transfer) |
Speed-up (Filtering) |
Speed-up (Overall) |
|---|---|---|---|---|---|
| global | 1640.47 | 17.71 | 4.60 | 92.6X | 73.5X |
| constant | 1638.44 | 10.56 | 4.67 | 155X | 107X |
| shared | 1642.94 | 4.73 | 4.67 | 347X | 174X |
| Table 4. The computation times of the developed kernel functions for the Gaussian filter. These kernel functions are referred as global, constant and shared, respectively. The unit is [ms]. Note that the computation times varied by trial because the non-real OS (Linux) was used. |
*Figure 6. The result of the Gaussian filter by the GPU.*
You can find the code used to compute the results at https://github.com/NaoyukiIchimura/cuda_image_filtering_shared. In addition, the code including parallel implementation for color conversion, image filtering and postprocessing can be downloaded from https://github.com/NaoyukiIchimura/cuda_image_filtering.
That's it. I hope this article would help you to write programs running on GPUs.