ご挨拶
今日から始まりました Machine Learning Advent Calendar 2013 幹事の @naoya_t です。今年もよろしくお願いします。
(日本時間では日が変わってしまいました。大変遅くなり申し訳ございません。アルゼンチン標準時(GMT-3)にはぎりぎり間に合いました!)
このアドベント・カレンダーの記事内容は、パターン認識・機械学習・自然言語処理・データマイニング等、データサイエンスに関する事でしたら何でもOKです。テーマに沿っていれば分量は問いません。(PRML, MLaPP等の読んだ箇所のまとめ、実装してみた、論文紹介、数式展開、etc.)
執筆する皆さんも読むだけの皆さんも共に楽しみましょう!
本日のお題
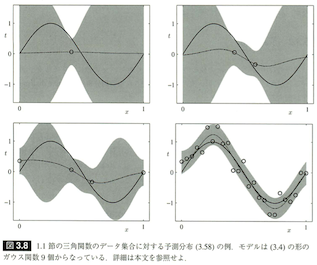
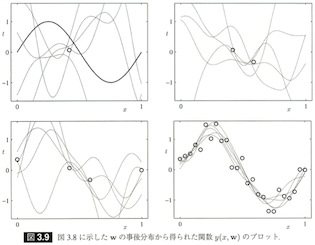
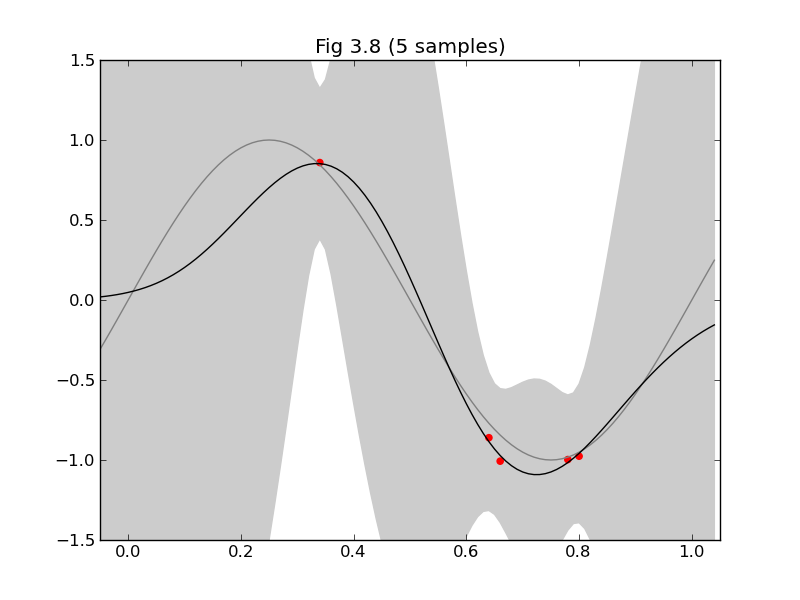
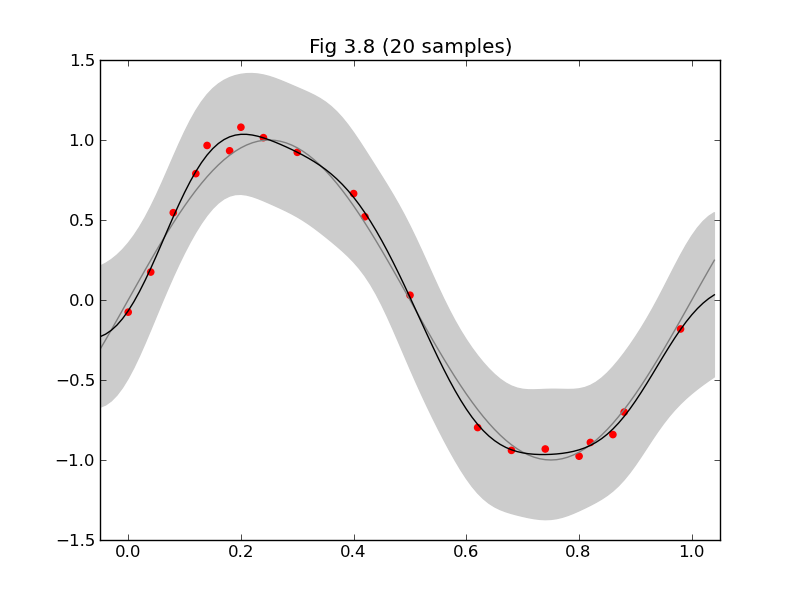
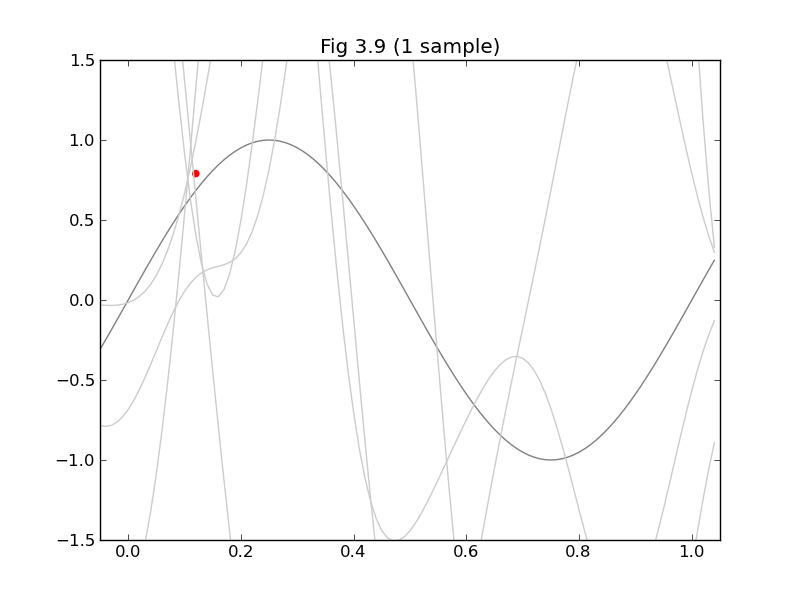
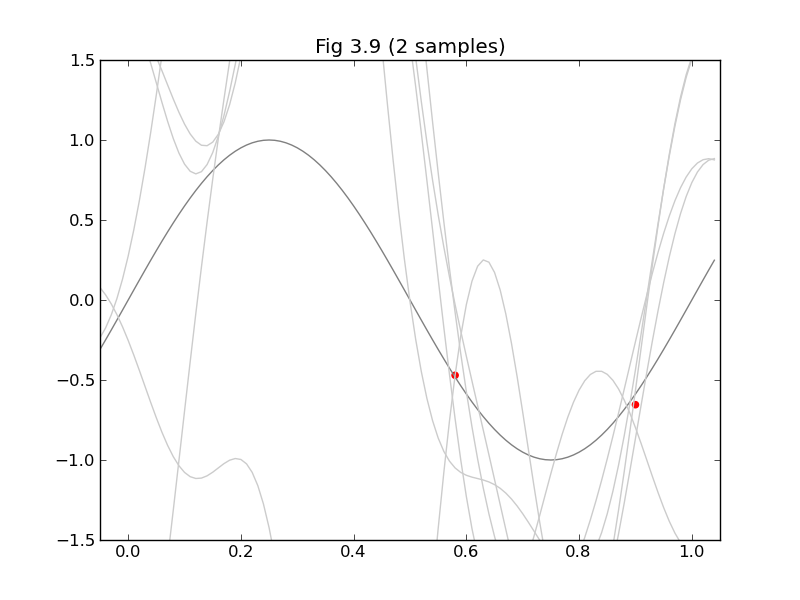
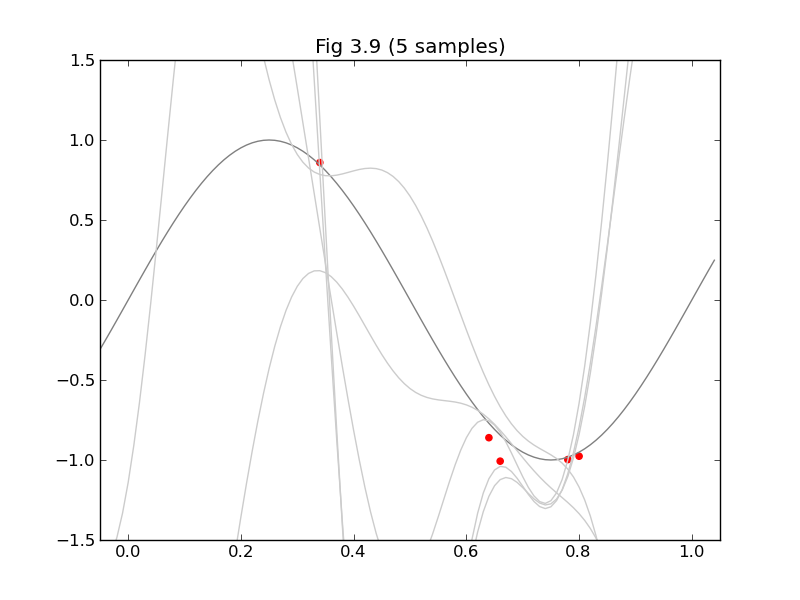
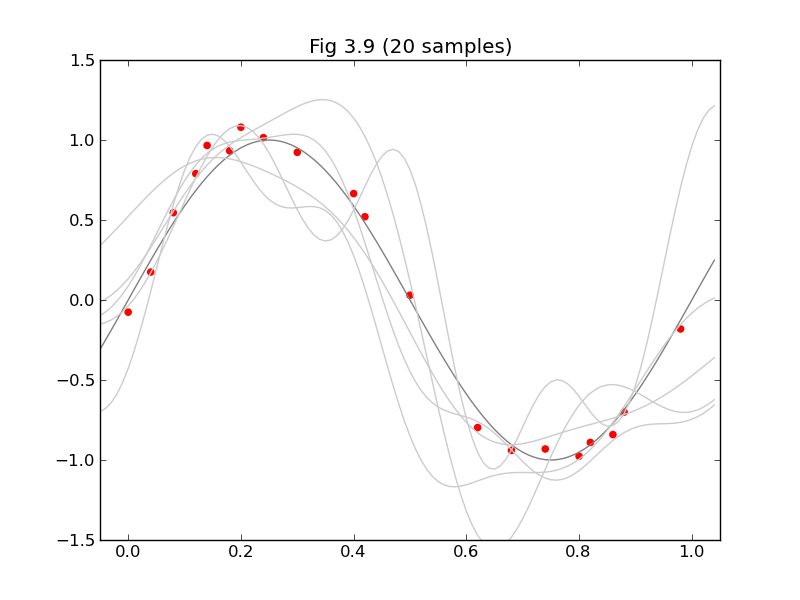
今日は、みんな大好きPRMLから軽めの話題ということで、§3.3の「ベイズ線形回帰」から、図3.8と図3.9を再現してみたいと思います。
等価カーネルの3Dグラフ(図3.10)も描こうと思っていたのですが時間切れでした。(気が向いたら追記します!)
必要な計算
図3.8のキャプションに「モデルは (3.4) の形のガウス(基底)関数9個からなっている」とあるので、
ガウス基底関数 $\phi_j(x)=exp\left(-\frac{(x-\mu_j)^2}{2s^2}\right)$ を x=[0,1] の範囲で適当に(というか均等に)9個並べてみることにします。
図3.8は予測分布 $p(t|\mathbf{x},\mathbf{t},\alpha,\beta)=N(t|\mathbf{m}_N\mathbf{\phi(x)},\sigma_N^2(\mathbf{x}))$ (3.58) の平均と分散が出せれば描けます。これに必要な
$\mathbf{m}_N$, $\mathbf{S}_N$, $\sigma_N^2(\mathbf{x})$ は
- $\mathbf{S}_N^{-1}=\alpha I+\beta\Phi^\mathrm{T}\Phi$ (3.54)
- $\mathbf{m}_N=\beta\mathbf{S}_N\Phi^\mathrm{T}\mathbf{t}$ (3.53)
- $\sigma_N^2(\mathbf{x})=\frac1\beta+\mathbf{\phi(x)}^\mathrm{T}\mathbf{S}_N\mathbf{\phi(x)}$ (3.59)
で求まります。ここで出てくる$\Phi$は皆さんお馴染みの計画行列 (3.16) です。基底関数 $\phi_j(x)$ と入力データ$\mathbf{x}$ から組み上げます。
図3.9は$\mathbf{w}$の事後分布 $p(\mathbf{w}|\mathbf{t})=N(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N)$ (3.49) から$\mathbf{w}$を5つずつサンプリングして、それぞれについて$y(x,\mathbf{w})=\mathbf{w}^\mathrm{T}\mathbf{\phi(x)}$をプロットするだけです。
コード
# !/usr/bin/env python
# -*- coding: utf-8 -*-
from pylab import *
S = 0.1
ALPHA = 0.1
BETA = 9
def sub(xs, ts):
# φj(x) にガウス基底関数を採用
def gaussian_basis_func(s, mu):
return lambda x:exp(-(x - mu)**2 / (2 * s**2))
# φ(x)
def gaussian_basis_funcs(s, xs):
return [gaussian_basis_func(s, mu) for mu in xs]
xs9 = arange(0, 1.01, 0.125) # 9 points
bases = gaussian_basis_funcs(S, xs9)
N = size(xs) # データの点数
M = size(bases) # 基底関数の数
def Phi(x):
return array([basis(x) for basis in bases])
# Design matrix
PHI = array(map(Phi, xs))
PHI.resize(N, M)
# predictive distribution
def predictive_dist_func(alpha, beta):
S_N_inv = alpha * eye(M) + beta * dot(PHI.T, PHI)
m_N = beta * solve(S_N_inv, dot(PHI.T, ts)) # 20.1
def func(x):
Phi_x = Phi(x)
mu = dot(m_N.T, Phi_x)
s2_N = 1.0/beta + dot(Phi_x.T, solve(S_N_inv, Phi_x))
return (mu, s2_N)
return m_N, S_N_inv, func
xmin = -0.05
xmax = 1.05
ymin = -1.5
ymax = 1.5
#
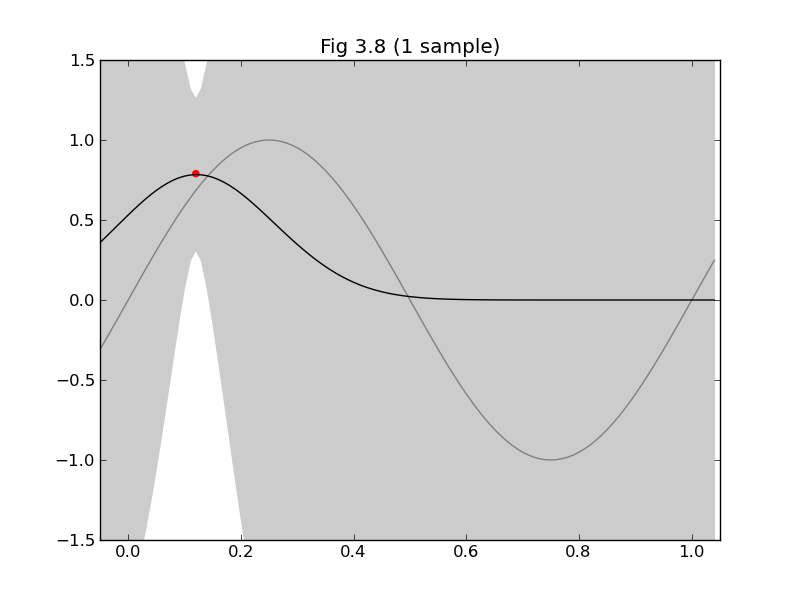
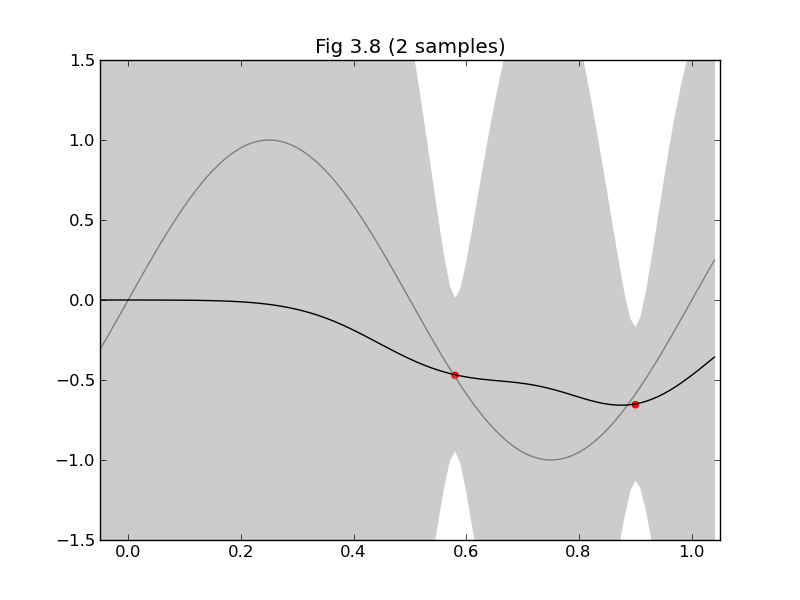
# 図3.8
#
clf()
axis([xmin, xmax, ymin, ymax])
title("Fig 3.8 (%d sample%s)" % (N, 's' if N > 1 else ''))
x_ = arange(xmin, xmax, 0.01)
plot(x_, sin(x_*pi*2), color='gray')
m_N, S_N_inv, f = predictive_dist_func(ALPHA, BETA)
y_h = []
y_m = []
y_l = []
for mu, s2 in map(f, x_):
s = sqrt(s2)
y_m.append(mu)
y_h.append(mu + s)
y_l.append(mu - s)
fill_between(x_, y_h, y_l, color='#cccccc')
plot(x_, y_m, color='#000000')
scatter(xs, ts, color='r', marker='o')
show()
#
# 図3.9
#
clf()
axis([xmin, xmax, ymin, ymax])
title("Fig 3.9 (%d sample%s)" % (N, 's' if N > 1 else ''))
x_ = arange(xmin, xmax, 0.01)
plot(x_, sin(x_*pi*2), color='gray')
for i in range(5):
w = multivariate_normal(m_N, inv(S_N_inv), 1).T
y = lambda x: dot(w.T, Phi(x))[0]
plot(x_, y(x_), color='#cccccc')
scatter(xs, ts, color='r', marker='o')
show()
def main():
# サンプルデータ(ガウスノイズを付加します)
xs = arange(0, 1.01, 0.02)
ts = sin(xs*pi*2) + normal(loc=0.0, scale=0.1, size=size(xs))
# サンプルデータから適当な個数だけ拾う
def randidx(n, k):
r = range(n)
shuffle(r)
return sort(r[0:k])
for k in (1, 2, 5, 20):
indices = randidx(size(xs), k)
sub(xs[indices], ts[indices])
if __name__ == '__main__':
main()
できた!
終わりに
去年は初日から飛ばし過ぎ的な指摘があったので、という訳ではなく執筆時間的な都合なのですが、今年はちょっと軽めなテーマ設定で皆さんのご期待に添えず申し訳ありません><
12/2の担当は @puriketu99 さんです。乞うご期待!