これは何か、誰を対象としているか
本記事は、私の検索機能のランキングアルゴリズム改善の経験則を、半ば後付けで定式化したものです。独学で身につけたものも多く、不正確・不勉強な記述があってもおかしくないので、コメント等で補足いただけるとありがたいです。
以下のような課題感がある方を対象にしています。
(1) ECサイトやらフリマアプリやら就活サイトなどの垂直型検索を対象とし、
(2) nDCGの改善ではなく、ユーザーにコンバージョン(CV)改善が目標
よくある情報検索(Information retrieval)の公開文献では
(1) 図書館の蔵書検索や、水平検索課題が念頭におかれている
(2) 確立されたベンチマークなどによる部分的な問題の深化
であることが多く、私含めて上記のような問題に直面している方には、応用のために少し工夫が必要だと感じています。本記事は、そのための工夫について書かれています。
すでに確率や機械学習、情報検索の基本的な概念を学習済みの方を想定しており、専門用語などの解説が手薄になっております。そこで、末尾に参考文献をまとめました。もし本記事の用語等で不明なものがあれば参考文献を一読を強くオススメします。
本記事の情報検索関連の訳語は、情報検索|森北出版株式会社に可能な限りあわせています。
本記事ではランキングアルゴリズムに焦点を当てるため、再現率に課題が少ない状態を前提としています。再現率に課題がある場合は、tokenizeの方法の見直し(2-gramの導入など)や、synonymの充実(いわゆるキーワード辞書の整備)や、表記揺れ(ヴィとビなど)などといった方法により改善ができますが、ランキングアルゴリズムでは改善されません。
言語モデルアプローチについて
情報検索|森北出版株式会社の第9章によると、
$p(Q=q, D=d, r=1)$ を最大化するために、$p(Q=q|D=d,r=1)p(D=d,r=1)$ の形に分解し、前者の$p(Q=q|D=d, r=1)$を求める形で、クエリに対して最も関連度の高いドキュメントを探す方法を「言語モデルアプローチ」と称するそうです。
ここで、$q$はクエリを、$d$は検索対象のドキュメントを、$r=1$は関連性の有無(1だと関連あり)を示します。つまり、$p(Q=q|D=d, r=1)$は「ある関連するドキュメントdが与えられた時のクエリがqだった確率」を示します。
クエリに対して最も関連度の高いドキュメントを探すためには、直感的には、$p(r=1|Q=q,D=d)$ 、つまり「あるクエリqとあるドキュメントdを与えた時に関連する確率」を求めたくなります。
もしくはランキングアルゴリズムに直接的に関連しそうな $p(D=d|Q=q,r=1)$、つまり「ある関連したクエリqが与えられた時にそれがドキュメントdである確率」の方が一見自然に思えます。
この条件付き確率の違いをわかりやすくするため、以下の人工的な例を考えます。
| | 美味しいカレー(c) | 癖のあるレバー(l) |
|:-:|:-:|:-:|:-:|
| クエリA | 7 | 3 |
| クエリB | 8 | 2 |
| クエリC | 6 | 4 |
ドキュメントに該当するのが、横軸の料理で、今回は「美味しいカレー(c)」と「癖のあるレバー(l)」しかないとしましょう。
表の数字は「注文回数」で、ここから関連度を推定するとします。実際のサービスではクエリとドキュメントの関連度を直接観測はできないため、クリックスルーログから推定することも多く、そこまで不自然ではない状況設定かと思われます。
ここで、$p(D=d|Q=A,r=1)$を考えると、$p(D=c,r=1, Q=A)=7/(7+3+8+2+6+4)=7/30$で、$p(Q=A,r=1)=(3+7)/(3+7+8+2+6+4) = 10/30$ でベイズの定理から $p(D=d|Q=A,r=1)=p(D=c,r=1, Q=A)/p(Q=A,r=1)=(7/30)/(10/30)=7/10$ であることがわかります。
同様に計算すると、
$p(D=l|Q=A,r=1)=3/10$
となり、クエリAが与えられた時にもっとも関連性の高いものは「美味しいカレー」となります。
一方で、言語モデルアプローチ($p(Q=q|D=d,r=1)$)だと、
p(Q=A|D=c,r=1)=p(Q=A,D=c,r=1)/p(D=c,r=1)=(7/30)/((7+8+6)/30)=1/3
p(Q=A|D=l,r=1)=p(Q=A,D=l,r=1)/p(D=l,r=1)=(3/30)/((3+2+4)/30)=1/3
とカレーとレバーが同じ数字になります。クエリCだとより顕著で、癖のあるレバーが美味しいカレーよりも高くなります。つまり言語モデルアプローチの考え方だと、クエリCではレバーが選ばれます。
これは、$p(Q=q,D=d,r=1)=p(Q=q|D=d,r=1)p(D=d,r=1)$の右辺の$p(D=d,r=1)$が消えているため、いわば相対的な関連度が高いものが選ばれるようになっていると解釈できます。逆に $p(D=d,r=1)$は絶対的な関連度(料理の例で言えば注文回数に影響する「人気」に対応≒人気度)とみなせます。
ランキングアルゴリズムを考慮する際に、クエリに対する相対的な人気度と絶対的な人気度を分離して考えることは以下の2点から重要です。
(1) 関連度を推定する際に、既存のアルゴリズムの表示順によるバイアスや登録期間の長さなどの外的要因による影響を $p(D,r=1)$にある程度限定化できる(完全にではないが)
(2) $p(Q=q,D=d,r=1)$を最大化するだけではなく、検索結果に表示させたいドキュメントはある程度ばらつかせたい場合、p(Q=q|D=d,r=1)の影響を大きくすることである程度実現できる
(1)は、例えばレバーが新商品だったため、カレーと比べて注文回数が少なく、その結果、ランキングアルゴリズムでもカレーの方が優先され、ますますレバーが注文されなくなる場合、などです。これは明らかに関連度を真に反映しているとは考えにくい状態です。
(2)は下記のスライドのp66 あたりがわかりやすいので、そちらを参考にしてください。
https://www.slideshare.net/shuryouchida/ss-133351464
そのため、実際のサービスでのランキングアルゴリズムでは「クエリに依存する相対的な箇所」と「クエリに依存しない絶対的な箇所」を意識的に分けて、それのバランスをとる(例えば、重み付け線形和などで)でひとつの重要な要素になります。Google検索もページランクという明らかに「クエリに依存しない絶対的な箇所」を設けていました。
では、この言語モデルアプローチの考え方で十分かと言われれば、やはり $p(Q=q|D=d,r=1)$に不自然な印象をぬぐえません。これをクエリの生成モデル(generalized model)とみなす考えもあるようです。
しかし、クエリの生成モデルだとすると、実際のユーザーは関連する具体的なドキュメントを思い描きながらクエリを組み立てるのではなく、もう少しふわふわした(いわゆる)情報欲求からクエリを生成している場合も多いはずです。(例えば具体的な商品をピンポイントで欲しい!ではなく、「お買い得なインスタントラーメンをまとめ買いしたい」など)
具体的なドキュメントが思い浮かんでいる場合の方を情報欲求の極端な場合とみなし、クエリは情報欲求から生成されるとしたさいに、どのような生成モデルになるかを念頭にし、次は構造的因果モデルによるアプローチを考えます。
言語モデルアプローチの考え方のように「どの部分の確率を扱っているか」を適切に分解できれば、ちょっとの工夫で現実世界の制約を対処できるので、とても便利です。ただ、この「ちょっとの工夫」を「なぜそうしたのか」「どの部分にどんな仮定をおいたか」を明確にするためにも構造的因果モデルによるアプローチは有益です。
構造的因果モデルによる提案手法について
ここからが今回の提案手法です。
構造的因果モデルとは、Pearl流因果推論ともよばれるここ30年くらいの比較的新しい統計的アプローチの基本となる方法です。これにより介入効果の推定や反事実を扱うことができます。
簡単にですがそのエッセンスもQiitaに投稿したので、そちらもお読みいただけると嬉しいです。今起きている革命、「因果革命」とは
構造的因果モデルの詳細をここで紹介するには少し重めなので、構造的因果モデルについて聞きなれない方はぜひ末尾の参考文献を参照していただければ、と思います。今回の記事は構造的因果モデルについて既知だとして、その専門用語を特に解説せずに用いるのでご容赦ください。
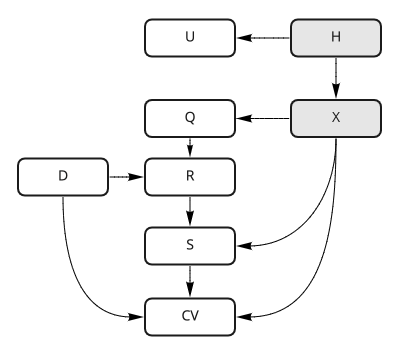
まず、今回仮定した因果ダイアグラムです。
U: デバイスや検索時刻、過去の検索行動などのユーザーについてのデータ諸々。この記事の図2.1のOnline ranking signals と同じものです。
H: 本サービスで検索機能を利用する人。観測不可能
X: 情報欲求。観測不可能
Q: クエリ。ここでは検索キーワードだけでなく、商品ジャンルによる絞り込みなども含む
D: ドキュメント
R: 検索位置。1以上の正の整数
S: 検索結果ページでユーザーに見られたか。1だと見られ、0だと見られていない2値変数
CV: 1だとコンバージョンし、0だとしていない2値変数
検索のランキングアルゴリズムの変更は、クエリとドキュメントが与えられた時のそのドキュメントの検索位置を変更するので、Rへの介入と見なせます。
まず、A/Bテストで既存のランキングアルゴリズムよりもCV性能の良いアルゴリズムを発見する、という課題を考えます。
その課題は $p(CV=1|do(R=new))>p(CV=0|do(R=original))$ となる$do(R=new)$を探すことになります。
$p(CV=1|do(R=new))$を展開すると
p(CV=1|do(R=new))= \sum_X \sum_D p(CV=1|S=1,X,D)p(S=1|R,X)p(R=new|D,X)p(D)p(X) = \sum_X \sum_D p(CV=1|R=new,X,D)\sum_Q p(R=new|D,Q)p(Q|X)p(D)p(X)
となります。
ここで確率の意味するところを見ていくと下記のようになります。
$p(CV=1|S=1,X,D)$ : 情報欲求XがあったときにドキュメントDを検索結果画面で見られた時にCVする確率。これを最大化することが目標になります。なお、見られていない場合($S=0$)はCVしないもの($CV=0$)としています。これは検索ランキングアルゴリズムの介入効果を推定したいという動機からは自然です。
$p(S=1|R,X)$ : 平たくいうと情報欲求Xに対して、検索位置の何番目まで見るか、という確率です。検索結果ページをどこまでスクロール(もしくはページング)するかは情報欲求だけが原因だと仮定を置いてます。Rが大きくなるとこの確率は下がっていきます。
$p(R=new|D,Q)$ : ドキュメントDとクエリQが与えられた時の検索位置の確率。ランキングアルゴリズム変更により介入できる箇所。$p(CV=1|S=1,X,D)p(S=1|R,X)$を最大化するRの時に、この関数を1に近づけることが目標になります。
$p(Q|X)p(X)=p(Q,X)$ : クエリQと情報欲求Xの同時確率。検索ランキングアルゴリズムへの介入では、ユーザーの情報欲求やそのクエリには直接干渉できないので、これは与えられたものとして、ここへの介入はスコープ外とみなします。Xは観測できないので $p(X|Q,H)p(Q)p(H|U)p(U)$の形で推定を行います。
$p(D)$: ドキュメントDの存在確率。検索ランキングアルゴリズムへの介入では、やはり直接干渉できないので、これも$p(D=d)=1$と存在するものとして扱います。
では、実際にどのようなランキングアルゴリズムを作れば良いかについて考えていきます。
計算可能にするため、モデルを仮定していきます。
最適化の方法
今回の提案手法の手順です。
- クエリ(Q)やユーザー情報(U)から情報欲求(X)を推定する($p(X|Q,H)p(H|U)p(U)p(Q)$)。Xで層別化するため、Xは離散のカテゴリーとします
- CVに至った検索結果画面に表示されたドキュメント(D)、そのランク位置(R)、どのドキュメントがCVしたかのログを収集する
- 上記のログから、CVしたドキュメントを正例、同じログでCVしないand(ランク位置がCVしたドキュメントよりも低いorランク位置が1~3程度)のドキュメントを負例とし、正例と負例のペアを作る
- 正例と負例のペアを推定した情報欲求で層別化する
- 情報欲求とドキュメントの対から特徴量のセットを計算する ($\{f_i(d_j),...f_k(d_j\}$と表記)
- その特徴量が与えられた時に正例だと1、負例だと0 を返す線形モデル($M$)を機械学習(ロジスティック回帰や線形SVM)で獲得する。L1-normをきかせるなどし、スパース解に近い方が望ましい
- 学習させたモデルをオフラインで評価(例えば、1月のデータで学習し、2月のデータでのAUCをみる)しながら、特徴量の作り方や情報欲求の推定の仕方などをオフライン指標が改善される方向に探索する
- 「クエリに依存する相対的な箇所」と「クエリに依存しない絶対的な箇所」の調整をする。情報欲求で層別化しなかった場合のモデルを計算し、その出力に適切な重みづけをし、線形和を取る
- 学習させたモデルを実装し、実際のシステムで $p(CV=1|D,X,S=1)p(S=1|R,X)p(R|D,Q)p(Q|X)$が向上するような $p(R|D,Q)$になっているかを過去ログから確認する
- A/Bテストを実施し、$p(CV=1|D,X,S=1)p(S=1|R,X)p(R|D,Q)$の各確率が計測結果からの推定(観測)とモデルによる予測(理論)の間でどこにどのくらいのギャップがあるかを調査する。なお、$p(D)p(Q|X)p(X|H)p(H|U)p(U)$は観測から推定する
- 上記を繰り返し、観測結果と理論のギャップを埋め、構造的因果モデルの完成度を上げる。
手順2~4の箇所が特に仮定や前提が入り組んでいるところです。そこが何を仮定したものかに興味がそこまでない方は下記の手順2~4の解説については読み飛ばしても実用上はあまり問題ありません。なお、本提案手法では、いくつかの近似や前提違反があるためこのままでは残念ながら完全な構造的因果モデルの獲得には至りません(Future work)
手順1: 情報欲求Xの推定方法について
今回の$X$は層別化して分析するため離散のカテゴリーを推定する問題としています。本当の $X$ は離散のカテゴリーでは表現できない可能性がありますが、今回は計算可能性を重視し、離散のカテゴリーで十分近似できるものだとみなして話を進めます。後の特徴量作成の箇所では、この仮定を少しだけ緩めた話もします。
因果ダイアグラムの矢印から、$p(X|H)$ が最大になる$X$を計算すれば良いことがわかりますが、$H$は観測できないため、$p(X|H)p(H|U)p(U)$と$U$から間接的に推定することになります。
そこで、$p(X|Q)$と、$p(X|CV=1,D,S=1)$の結果からの原因推定(アブダクション)も組み合わせて、少しでも推定精度を高めます。
今回のXの推定の目的やその評価は $p(CV=1,D,X,S=1)$ の最大化で得られるため、$p(X|CV=1,D,S=1)$を基準に $X$のカテゴリーを作ります。これはコンバージョンされたドキュメントの情報から、情報欲求のカテゴリーの分け方を求める、とも言えます。
もっとも単純にはドキュメントを情報欲求に関連しそうな”いい感じ”に特徴量化し(ECサイトなら商品ジャンルや価格帯など)、教師なし学習(クラスター分析など)を用いる課題になります。しかし、単に教師なし学習を適用しただけではそのカテゴリー化がどのくらい妥当かの評価が困難です。ここで、「同一のユーザーは一定の期間の間は情報欲求は変わらない」という仮定をおけるなら、半教師あり学習となり、部分的にですが情報欲求のカテゴリー分けの仕方について評価ができます。しかし、サービスの性質によってはその仮定を置くことが難しいです(ほしいものは1つだけなのでひとつの情報欲求ではひとつのドキュメントしかCVしない場合など。家探しや職探しのようなサービス内では複数候補を絞るだけ、な場合は有効である可能性あり)。そこで、出力が確率である機械学習モデルを使って、以下の対数オッズが大きい方がいい、といった評価するといった工夫(強化学習の問題設定になる)も考えられます。
log(\frac{p(X|CV=1,D,S=1)}{p(X|CV=0,D,S=1)})
これで情報欲求Xのカテゴリーの種類が定まったら、次は $p(X|Q,U)$ を求めます。なぜなら、実際に検索実行時にランキングアルゴリズムで推定した$X$ を用いるさいには、$p(CV=1,D,X,S=1)$は未来の情報になるため使えないからです。
今度は$X$が推定できているため、教師付き学習(カテゴリー分析)の課題になります。クエリやユーザー情報の特徴工学(feature engineering)やモデル選択などが重要です。Kaggleなどで発展している技法が使えます。
手順2~4: 学習データの作り方の仮定について(詳細)
情報欲求のモデル
最初に、Xをどう扱うかについて固めます。まずシンプルに、情報欲求の取りうる値をドキュメントの和集合だとみなし、コンバージョンしたならば、その情報欲求にそのドキュメントが含まれていたとします。
先程までの確率の言葉で書くと、$p(d_j \in x_i | CV=1,X=x_i, D=d_j, S=1)=1$ です。
一方、$p(d_j \in x_i | CV=0,X=x_i, D=d_j, S=1)$は0とは限りません。情報欲求に含まれるドキュメントだとしても「他にもっといいものがあり1つだけ欲しかった」といったCVしない可能性は想像できるからです。とはいえ、1よりかは低いでしょう。
対偶をとると、$p(CV=0 | d_j \notin x_i,X=x_i, D=d_j, S=1)=1$で、これは $p(CV=1 | d_j \notin x_i,X=x_i, D=d_j, S=1)=0$ ということですから、$p(d_j \notin x_i,X=x_i, D=d_j, S=1)$をできる限り下げたい、となります。つまり、情報欲求に含まれないドキュメントはユーザーに見える確率を下げたい、となります。
さらに、$p(d_j \notin x_i , X=x_i, D=d_j, S=1)+p(d_j \in x_i,X=x_i, D=d_j, S=1)=p(x_i,X=x_i, D=d_j, S=1)$であり、両辺を$p(x_i,X=x_i, D=d_j, S=1)$でわって、$p(d_j \notin x_i | X=x_i, D=d_j, S=1)+p(d_j \in x_i|X=x_i, D=d_j, S=1)=1$
なので、$p(d_j \in x_i|X=x_i, D=d_j, S=1)$をできる限り増やしたいともなります。
次に、$p(d_j \in x_i|X=x_i, D=d_j, S=1)$を推定を考えます。この条件付き確率は、CVで条件付すると以下のような関係になります(一番最初に書いてある条件からです)。
p(d_j \in x_i|CV=1, D=d_j, X=x_i, S=1) > p(d_k \in x_i|CV=0, D=d_k, X=x_i, S=1)
この関係式を満たすものを考えます。
これは実際の検索結果ページのログから「同じ検索結果ページのドキュメントのうち、CVされたものとされなかったものを予測」する課題、Learning to Rank で pair-wiseとよばれる学習データの生成方法と似た形になりました。右辺が未知のためにpoint-wiseのような絶対的な値への回帰ではなく、pair-wiseのような相対比較の形になりました。
同じユーザーの同じクエリの同じ検索結果ページならば情報欲求も同じはずです。通常のpair-wise法と違うところをはS=1で条件づけされているところです。これは情報欲求ごとにどのくらいまでの検索結果位置まで見られるか、といった推定をする場合、ページスクロール率といったフロントエンドのログを情報欲求で層別するなどの分析が必要になります。それが大変な場合は、「画面デザイン的に上位2,3件は間違いなくみるだろう」といった仮定を起き、CVしなかった負例は検索結果位置が1~3番目のものやCVしたものよりも上位のものだけ使う、といった工夫で回避できるはずです。つまり$p(S=1|R<3,X)=1$といった仮定を置きます、(2021/7/15 修正:pair-wiseと書くところをList-wiseにしていたため修正)
情報欲求とドキュメントの関連度のモデル化
今度は$ p(d_j \in x_i)$ を計算するためにこの関数のモデルを仮定します。
先ほどは、 $X$ を$D$ の集合としましたが、この集合が生成される過程を想像します。おそらく、我々の情報欲求は「暖かい食べ物 or 麺類」「調理が簡単なもの」「1食200円以内で安いほど嬉しい」「保存がきく」といった特徴の集合で作られています。具体的な商品が欲しい場合も、「商品名はhogehoge」といった極端な特徴だとみなせなくもないです。そこで、$d_j \in x_i$ をそのドキュメントが「どのくらいその特徴と合致するか」「その特徴の関連度の重要度」によってモデル化できるとします。
$ d_j \in x_i $の真偽値は
\prod_{i' \in i}(f_{i'}(d_j))^{w_{i'}} > \alpha
ならば tureで、そうでなければfalse とします。
もしくは両辺に $log_2(x+1)$をとって、
\sum_{i' \in i}{w_{i'}}f'_{i'}(d_j)>log_2(\alpha +1)
ここで $f_{i'}(d_j)$は$x_i$を構成するある特徴とドキュメントの関連度で、0から1の値を取るとします。
$w_{i'}$ はその特徴の重要度であり、実数です。全く重要でないときは0をとり、満たすべきでない特徴のときは負の数になります。$\alpha$は適当な定数です。
ここまでのモデルを組み合わせると、「同じ情報欲求のとき、CVしたドキュメントではCVしなかったドキュメントよりも
\sum_{i' \in i}w_{i'}f'_{i'}(d_j)
が大きくなるような、$w_{i'}$と$f_{i'}(d_j)$ を求めれば良い、となります。そして、この値をそのままランキングアルゴリズムのスコアに用います(スコアが高いほど上位に表示されます)。
手順5: 特徴量の作り方について
$f_{i'}(d_j)$ さえ求めれば、$w_{i'}$ は教師付き機械学習によって求められます。
この問題は特徴工学とよばれる、知恵と根気と経験が強く求められるものになります。特徴工学には試行錯誤が求められます。理論的に導出することが非常に困難であるため、ここではどのような特養量が考えられるかの例を提示します。
ちなみにGoogleではこの箇所のことを signal とよぶそうです。
あくまで経験則ですが、これらの特徴量をランキングアルゴリズムに組み込むことで実際にA/Bテストにより有意な改善を確認した経験があります。
例1: ドキュメントの絶対的な人気度
「こだわり」の少ない場合、定番の人気商品は重要な選択肢になりがちです。
おそらく人気度は $p(CV=1|D,S=1)$ や $p(CV=1,S=1,D)$ に表れ、前者はいわゆるコンバージョンレート(CVR)、後者はCV数に比例します。
例2: ドキュメントの新鮮さ
「こだわり」の強い場合や、ドキュメントの在庫が少ない場合など、情報欲求やサービスの特性により、ドキュメントの新鮮さが重要な場合があります。ドキュメント追加から検索時の経過時間に対して単調減少する関数や、一定期間をすぎたら0になる矩形波関数など、どのように減衰すべきかには選択肢があり、データ(もしくは直感)によって決める必要があります。
例3: 典型的な価格の近さ
ECサイトなどの場合「このくらいの価格なら買う」といった情報欲求が存在します(自己の経験談)。
その場合、情報欲求から「このくらいの価格」を推定し、それよりも安い(あるいはその価格に近い)ドキュメントはこの特徴に関連すると見なします。
例4: クエリ文字列が構造化されたドキュメントの特定のフィールドに含まれる
例えば、特定のエリアのお店を探しているとしましょう。さらにドキュメントが「店名」「営業時間」「所在地」などのように構造化されているとしましょう。その場合、クエリに入力された文字列が「所在地」に含まれている場合、そのドキュメントはその情報欲求に関連していると見なします。この場合の「含まれている」とは、文字列の部分一致や、tokenの完全一致、BERTなどによるword embedding空間での近さなどなど、自然言語処理課題の一種として捉えられます。
この特徴量の計算に「情報欲求」ではなく「クエリ」を用いたため、推定するために離散化された情報欲求よりも、より細かい情報欲求を表現できる可能性があります。他にもユーザー情報に関連する情報を引数にするなど、特徴量の工夫次第では情報欲求をカテゴリーで表現したためにおきた情報ロスをある程度救うことができます。
手順6~7: 機械学習について
特徴工学が済んだ後は、機械学習を使って学習させます。線形モデルをベースとした2値判別問題なので、線形ロジスティック回帰や線形カーネルSVMで解くだけです。実装のことも考えると $w$ がスパースになると嬉しいので、L1-normを含めた最適化計算をお勧めします。個人的にはLIBLINEARを高速かつメモリ消費量が少ないため10年近く愛用してます。
以下は、線形モデルという「制約」が気になる方向けの説明です。
- 非線形変換は特徴量の計算($f$)で行える
- 多くの深層学習モデルも最終層は線形であることが多い
線形であることによって以下のメリットがあります
- モデル学習の計算が軽い
- 特徴量の解釈性が高い
- 複数モデルの結合も容易
- 実装が用意(全文検索エンジンに多くを任せられる)
メリットの1と2は自明だと思いますので、メリットの3は手順8、メリットの4は手順9で解説します
手順8: 相対と絶対のハンドチューニングについて
ここで、「言語モデルアプローチ」の箇所で触れた「クエリに依存する相対的な箇所」と「クエリに依存しない絶対的な箇所」の分離について再考します。
分離の必要性は (1)観測されたログに含まれる過去のランキングアルゴリズムのバイアスが「クエリに依存しない絶対的な箇所」に多く含まれると予想、(2)検索結果の多様性などの、同時確率$p(CV=1,D,X,S=1)$最大化以外の目的関数の存在、を理由にしました。
現在の因果ダイアグラムだと(1) $p(R|D,Q)$ の箇所に確かにバイアスが残る (2)そのほかの目的関数の存在が因果ダイアグラムに書かれていないため考慮できていない、といった課題があり、実用上「相対」と「絶対」の調整が重要になります。
手順5 の特徴量の例では、3,4が相対的、1,2が絶対的な箇所に該当するようにみえるため、「特徴量を相対と絶対の2つに分けて、片方の種類の特徴量の重みに調整のための係数をかける」といったナイーブな対応が考えられます。
しかし、「情報欲求」の種類によって例えば「ドキュメントの新鮮さ」の重要度は変わるとも考えられるため、上記のナイーブな対応は仮定を正確に反映していません。
ここでは、「情報欲求によって層別しなかったログで学習したモデルの出力に適当な係数をかけて引く」といった方法を提案します(割った後に対数を取るので引き算の形になる)。
この適当な係数がハイパーパラメータとなり、多目的最適化関数の変化の影響範囲をこの変数に集約することで、ビジネスの外的状況変化による変化に追従しやすくなります。この多目的最適化の話はAIアルゴリズムマーケティングという書籍が勉強になりました。
手順9: 実装とその性能のテストについて
ここでは実際に上記のモデルをどのように実装するかについて簡単に述べます。全文検索エンジンのOSSである Apache Solrを活用していく形を考えます。Elasticsearchでも似たようなことは可能です。
大雑把に
- 情報欲求の推定と関連する $w$ の計算
- $f_i(d_j)$ の計算
- $\sum w f_i(d_j)$ の計算
の3種類に分解でき、1番目の計算はSolrから見たときのクライアント側で実施、2番目の計算はドキュメントの更新のタイミングでバッチ処理的に計算しその値をSolrのindexに追加、3番目の計算はSolrで計算、とする方法がオススメです。
多くの人は3番目のSolrでの計算に馴染みが少ないようなので、そこだけを簡単に解説します
実は、Solr function queryという特殊なクエリを使えば、$\sum w f_i(d_j)$ の計算を簡単に表現できてしまいます。
例1: ドキュメントの絶対的な人気度
CVRやCV数がindexにあるのならば、Filed Functionでindexの値をそのまま参照でき、数式に組み込めます。
Elasticsearchでも類似機能があります。
例2: ドキュメントの新鮮さ
ドキュメントの更新時刻がindexにあるのならば、ms Functionで現在時刻との差分を取得できます。四則演算や対数変換などの関数も用意されているので差分の非線形変換もかけられます。
Elasticsearchの場合はいくつかの距離関数がデフォルトで用意されています。
例3: 典型的な価格の近さ
1番目の計算で重み $w$の推定の他に情報欲求から「典型的な価格」を求めておけば、それの値をクエリに入れて、Field Functionでドキュメントの価格の値を参照し、それをFucntion Queryの四則演算や対数変換で両値の距離を計算できます。
例4: クエリ文字列が構造化されたドキュメントの特定のフィールドに含まれる
exit Functionとquery Functionを組み合わせれば、Solrのtokenizer の範囲での文字列一致の判定結果をFunction Queryに組み込めます。
Elasticsearchの場合は少し思想が違い、field value factorなどのfilter機能を使い実装します。
このように線形モデルの場合は全文検索エンジンの機能を活用すれば容易に実装ができます。もう少し詳細に知りたい方は、Apache Solr入門の9章がオススメです(ダイマ)。
このよう本提案手法のランキングアルゴリズムは全文検索エンジンをベースとすれば比較的容易に実装可能です。実際に大規模なサービスで展開するさいはリソース監視やらインシデント時の対応やらの他に運用面で考えることはたくさんありますが、ひとまず $p(R|D,Q)$ が $p(CV=1|D,X,S=1)p(S=1|R,X)p(R|D,Q)p(Q|X)$が向上するようになっているかを手元で確認するのはそこまで技術的難易度が高いわけではありません。
ここで過去のQとDから実装が$p(R|D,Q)$を意図通りにコントロールできていることを確認してからA/Bテストを実施しましょう。
手順10~11: A/Bテストによる確認について
A/Bテストのやり方や正しく実施するためのtipsは既知とします。末尾の参考文献のA/Bテスト実践ガイドを未読の方はぜひ一度読んでみてください。
ここでは改めてA/Bテストの意義について確認します。
なぜならDとXを観測・推定可能であるとしているため、理論上A/Bテストなしでもランキングアルゴリズムの介入効果は推定可能だからです。
なぜA/Bテストの実施が望ましいのか。それは今回の構造的因果モデルがいくつかの点で不完全だからです。
不完全な点1: No Interference between subjects assumption が満たされない
今回、私が用いた構造的因果モデルでは No Interference between subjects assumption という仮定が成立している必要があります。今回想定している問題では、ほかのドキュメントの存在がコンバージョンに大きく影響するからです。すでになんども述べている、検索結果画面には多様性が重要といわれていることや、「ユーザーはどれかひとつにコンバージョンすれば十分」といった状況では、明らかにNo Interference between subjects assumptionが満たされていません。そしてこれは特殊な状況ではなくごく当たり前に起きる状況です。
ですので、今回の構造的因果モデルはその大前提から不正確になっています。とはいえ構造的因果モデルなしに定式化を進めるよりかは現時点ではあったほうがマシだと考えています。今後、統計的因果推論がNo Interference between subjects assumptionを満たさないケースでの理論や、情報検索で実用的な「検索結果の多様性のモデル」がより発展したら、改めて考えたいと思っています。(現時点では非常に難しいという印象があります)。
不完全な点2: 過去のランキングアルゴリズムによるバイアスが考慮されていない
実際に介入する際は $p(R|Q,D)$はこちらの自由にできます。しかし、ログからの最適化をするさいに $p(R|D,Q)$の影響を考慮に入れる必要がありますが、今回の最適化の手順ではその考慮が含まれていません。そこから受ける影響を軽減するため、「相対」と「絶対」の調整の箇所で経験則による工夫を入れてますが、介入効果の正確な推定という点ではその工夫はあまりに洗練されてなく、一段の熟慮が必要です。(不完全な点1よりかはまだ解ける問題な気がします)。
不完全な点3: ほかの目的について考慮されていない
「相対」「絶対」の議論でなんどか出てきたように、$p(CV=1,D,X,S=1)$以外にも目標がある場合があります。今回の因果ダイアグラムではほかの目標についての記述は出てきていません。
また、サービスの成熟度によっては多目的最適化のための目的関数がそもそも定義できていない場合もあります。このような場合は、実際にA/Bテストを重ね、潜在的な目的間のトレードオフ関係を議論と実験によりあぶりだすことが重要です(A/Bテスト実践ガイドの6章参照)。
これらの点から本提案手法は完全ではありません。
しかし、実際の観測結果とモデルによる予測のズレを見つけ、そこに対して工夫を重ねることで、(理論的には重大な欠点があるが)実用上問題ない構造的因果モデルの獲得ができるのではないかと楽観視しています。特にA/Bテストを実施した場合には、$p(R|D,Q)$が介入されたデータが手に入るため、$p(CV=1,D,X,S=1)$の予測が観測とずれた場合に、どこにずれがあったのかのデータ分析・探索がやりやすくなります。
これはまだ取り組み中の課題で私が知る限り成功事例がないため現時点では妄想でしかないのですが、その取り組みに成功した場合は、オフラインテストでのランキングアルゴリズム介入効果の正確な推定だけではなく、さらに大きな可能性が広がっていると考えています。
【発展】構造的因果モデルにより達成できることはランキングアルゴリズムの改善だけではない
最後に、正確な構造的因果モデルが実現した場合のメリットを挙げます。
メリット1: Hについて反事実の議論ができるようになる
「もし、H(サービス利用者)がこのくらいいたら、D(ドキュメント、商材と読み替えても良い)のコンバージョン(CV)はこのくらいになっただろう」が正確に示せるようになります。
これはサービスにとってマーケティングの目標設定がより明確になる効果があります。また、将来のH変化による影響も正確に予測できるようになります。特にCVがサービスにとって重要であればあるほど重要な点です。
メリット2: Dについて反事実の議論ができるようになる
「もしDがこのくらいあったら全体のCVはこのくらいになっただろう」が正確に示せるようになります。
これもサービスの特性にもよりますが、ビジネス上の戦略的意思決定に大きな影響のある情報だと思われます。
メリット3: ランキングアルゴリズムの介入効果をオフラインテストから正確に予測できるようになる
ランキングアルゴリズムの介入効果の予測は非常に難しく、Booking.comでは実際に試してみたが、全くうまくいかなったことを報告しています(文献リンク)。構造的因果モデルを用いれば「どこ」が予測と実測にズレがあるかを議論しやすくなるため、本アプローチは先行研究と比べその点が優位だと考えています。
オフラインテストでランキングアルゴリズムの介入効果を予測できれば、実施に時間がかかるA/Bテストの依存度を下げた状態で改善をまわせるので、ユーザー数がそこまでいないサービスでも、より高速かつ複雑なモデルでも最適化できるようになります。
メリット4: ほかの機能改善との関連性が明確になる
例えば、A/Bテスト実践ガイドで紹介されている「Bing検索での検索結果画面のタイトル文の変更」は$p(CV=1|D,X,S=1)$に対する介入(正確にはもう少し分解が必要そう)ですし、キーワード検索の入力フォームへのQuery Auto Complete機能(入力サジェスチョン)は、$p(Q|X)$への介入です。
このようにシステムの情報の流れがひとつの構造的因果モデルで記述できるようになれば、$p(CV=1,D,X,S=1)$から逆算して「どこをどう介入すれば良いか」がより明確になります。
ランキングアルゴリズム改善だけを考えた場合はメリット3が一番重要ですが、サービス全体を考えたら、その他のメリットの方が重要になるかもしれません。
ランキングアルゴリズムの改善を通じて、この有益な構造的因果モデルの完成度を上げていけるため(情報欲求の表現系と、ドキュメントと情報欲求の各要素との関連度と、情報欲求とドキュメントが与えられた時のCV確率の推定精度を上げられる)、私は検索機能の改善にはサービスにとって大きな可能性が眠っていると考えています。
参考文献
情報検索|森北出版株式会社
Googleのエンジニアの方が検索エンジンの実装から評価まで一通り書いた本。検索エンジニアを志す人にとって非常に勉強になる本です。
統計的因果推論|共立出版
Pearl氏のCAUSALITYの訳書です。数学3割哲学7割といった内容。将来、古典として歴史に残る本だと思います。
入門 統計的因果推論|朝倉書店
統計的因果推論の数学的操作について簡潔にまとまった本です。具体例もあり演習問題もあり実際に活用したい人にとってとても良い本でした。
The Book Of Why|Basic books
Pearl氏の一般書です。なぜ統計的因果推論が因果革命とよばれているかについて歴史的側面から解説した本。一刻も早い翻訳本が望まれます。
Apache Solr入門|技術評論社
Solr6を対象にしたため、内容は多少古くなっていますが、本記事のFunction Query活用関連はさほど古くなっていません。買ってください(ダイマ)
A/Bテスト実践ガイド|アスキードワンド
A/Bテストを正しく実施するための知恵の宝庫。買ってください(ダイマ)
AIアルゴリズムマーケティング|IMPRESS BOOKS
ビジネス観点から情報検索技術を紹介している本。アカデミックのそれとは違う視点でとても面白かったです。