今起きている革命、「因果革命」とは

みなさまは"The Causal Revolution" (因果革命)という言葉を聞いたことがあるでしょうか？
私は今月(2021年6月)に初めて知りました。Google Trendsでもデータ不足によりトレンドが表示されません。
つまりまだ全然マイナーな概念で、聞いたことがないほうが自然かと思われますが、これは「来る」と確信したため本記事を投稿しました。この確信の根拠の箇所を記事中で太字で書いた他、最後にもまとめたため、本記事を読む価値がありそうかの判断には先にそちらを読んでもらってもいいかもしれません。しかしながら、因果革命ないし統計的因果推論は学ぶ価値のある分野です。本記事を読まなくても下記に挙げた書籍を未読の方はぜひ一読してみてください。Qiitaでも因果推論についての記事はいくつもあります。しかし、私が感動した点を明示化した記事は見当たらなかったため本記事を投稿しました。

この記事のきっかけになった本

統計的因果推論｜共立出版
Pearl氏のCAUSALITYの訳書です。数学3割哲学7割といった内容。将来、古典として歴史に残る本だと思います。
入門　統計的因果推論｜朝倉書店
統計的因果推論の数学的操作について簡潔にまとまった本です。具体例もあり演習問題もあり実際に活用したい人にとってとても良い本でした。
The Book Of Why｜Basic books
Pearl氏の一般書です。なぜ統計的因果推論が因果革命と称するに値するかについて歴史的側面を中心に解説した本。一刻も早い和訳本が望まれます。
統計的因果探索｜講談社
上記のPearl氏の本では触れられていない「データから因果の矢印の向きをどのように推定するか」について書かれている本です。本書だけで完結する内容になっていますが、統計的因果推論は概念自体が新しいため、上記の本を読んだ後の方が理解しやすかったです。

因果革命

因果革命とは、ベイジアンネットワークや統計的因果推論の研究者であるJudea Pearl氏の著書、The book of whyで繰り返し出現する単語で、従来は"The Ladder of Causation(因果のはしご)"の最下部の"SEEING(観察)"研究でしか定式化できていなかったところを、その上の"DOING(行動)"や"IMAGINING(想像)" に属する研究でも定式化できるようになったことを指します。これにより、今後の研究（特に疫学や社会科学などのいわゆるソフトサイエンス）が飛躍的に発展し、病気の治療や政策決定の質が劇的に向上するという予期から「革命」という仰々しい単語が使われているようです（The Book of Why内では明確に定義されていなかったので私の解釈が混ざっています）。大流行したサビエンス全史で使われた"認知革命"やニュートンによる"科学革命"を意識した言葉で、「新たな概念を獲得することで、達成しうることが急激に増える」という点が同じです（因果革命が本当に革命と呼べるほどになるかは将来になってみないとわかりませんが）。

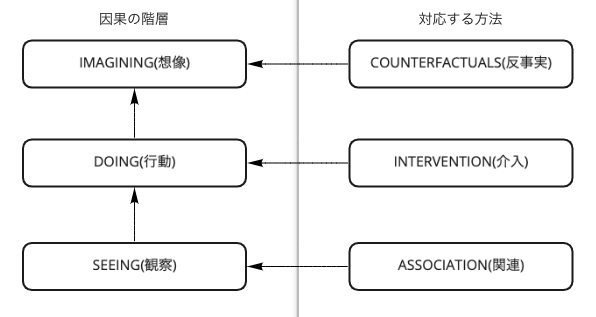
因果のはしご

「因果のはしご」とは、ヒトの因果関係の認知を3つの階層にわけたものです。下記の図1をご参照ください。このはしごを下から上にのぼるほど高度な能力が要求されます。Pearl氏の見解によると、「認知革命」は因果のはしごの一番上（想像）に到達した後に起きた出来事です。ヒトの因果関係の認知が実際にこのような階層になっていることや人類の躍進との関連性は証明できませんが、この3つの階層に対応する方法（反事実、介入、関連）が根本的に異なることは、Pearl氏の定式化によれば、数学的に証明可能です。従来の統計手法（深層学習といった最先端のものも含む）は関連の枠組みの中の話であり、介入や反事実とは質的に違う話とされています。いわゆる強いAIは「想像」のための反事実的な操作が求められるため、今の機械学習の方向性では強いAIは獲得できないとPearl氏はThe Book Of Why｜Basic booksで述べています。

図１　因果のはしご

この３つの違いについて「薬と病気の回復」の関係を例えにして簡単に解説します。これは「私の理解」というフィルターがかかっているため、より正確に詳細に知りたい方は冒頭に挙げた書籍を参照していただけると助かります。
統計的因果推論の技法を用いることで因果のはしごの各階層で下記のようなメリットがあります。

観察と関連にとって、交絡とそれによる調整方法の明示化
行動と介入にとって、無作為標本化実験ではない観察データからの介入効果の推定
想像と反事実にとって、「but for~」などの司法で実際に使われる概念の定量化

ができるようになります。これを簡単に解説します。

交絡とそれによる調整方法の明示化

薬を飲むか($d=1$)飲まないか($d=0$)と病気が回復するか($c=1$)しないか($c=0$)を観測します。すると $p(d,c)$ の同時確率が推定できます。
ここから、 $p(d,c)=p(d|c)p(c)=p(c|d)p(d)$ も計算できます。非常にナイーブに考えると、薬の効果は$p(c=1|d=1)-p(c=0|d=1)$ に表れるように見えますが、これは従来の統計学でも今回の統計的因果推論でも間違った解釈です。従来の統計学では、薬を飲むか飲まないかを無作為に決定した無作為標本化実験(Randomized Controlled Trial: RCT、Web業界だとA/Bテストと呼ばれる)のみ、因果関係を取り扱え、今回のデータがRCTにより得られた場合では、薬の効果が$p(c=1|d=1)-p(c=0|d=1)$ に表れると考えられます。ここの議論は次節に回すとして、今回のデータは議論を簡単にするためにRCTによって得られたものとします。

さて、この観察データから推定された薬と病気の回復の確率の関係をより詳しく調査していきましょう。

ここで、病気と薬の関係性に性差が影響あると考えられるとします。その場合、性別が交絡因子とみなせます。女性($s=0$)と男性($s=1$)ごとに条件付き確率を計算すると、$p(c=1|d=1,s=0)-p(c=0|d=1,s=0)$や $p(c=1|d=1,s=1)-p(c=0|d=1,s=1)$ が得られます。これを（性別による）「調整」と呼びます。
この「調整」をすることで、例えば「男性にとってこの薬は有害だが、女性にとっては有効」のような価値のある知識が得られるようになります。

では、次に病気と薬の関係性に血圧(b)が影響ある（交絡因子である）と考えられるとします。この場合は血圧で調整するのは妥当でしょうか？
答えは「観察データからはわからない」になります。この調整すべきか否かの考え方はかなり混乱を招きやすく、実際の研究でも調整すべきでないときに調整をしてしまっている例が多々見受けられるそうです。一番極端な考え方ですと「観測できる交絡因子に対してできる限り調整を行った方が望ましい」といったものまであるそうですが、これは誤りです。

Pearl氏は観測データと確率以外に、因果ダイアグラムと名付けた有向非循環グラフを導入することで調整すべきか否かを決定できるわかりやすい方法を提案しました。因果ダイアグラムでは従来の確率の言葉で表現できなかった原因と結果の非対称性を表現します。この確率と因果ダイアグラムによる定式化を構造的因果モデルとよんでいます。
統計学では嫌がられがちな原因と結果についての哲学的な議論について本記事では触れません。Pearl氏はそれに全力で突っ込みに行っているので、そちらに興味ある方は統計的因果推論｜共立出版をご参照ください。ここでは、「薬を強制的に飲ませた場合と飲ませなかった場合で病気が回復する確率が変化するか」を考え、変化した場合に薬は原因で、病気の回復は結果だとします。

今回、「病気の回復」が原因で、「薬」が結果であるケースはあり得ないものだとしましょう。もっと正確に言うと今回はRCTで得られたデータを想定しているため、「薬」の確率（薬を飲むか否か）の原因は他のすべてと独立な乱数しかありえません。

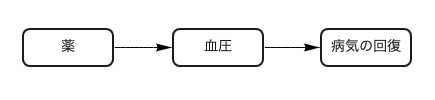
まず、「薬により血圧が変化し、それにより病気が回復する」といった因果関係を想定します。

図２ Chain(連鎖経路)の関係を示した因果ダイアグラム

線の向きは因果の方向を意味してます。つまり原因→結果
この場合では、血圧で調整をしてしまうと、薬と病気の回復が独立になってしまいます。本当は薬と病気の回復に因果関係があるにも関わらず、関係がないように見えてしまいます。これは調整すべきでないケースです。定性的・感覚的に解釈すると、例えば「薬を飲むと血圧が下がり、血圧が下がると病気が回復」という関係の時に、血圧の高低で条件付けしてしまうと、薬を飲む飲まないに関わらず「血圧が下がると病気が回復」の効果しか見えなくなり薬の影響が隠れてしまいます。
この関係性をPearl氏はChain(連鎖経路)と呼んでいます。

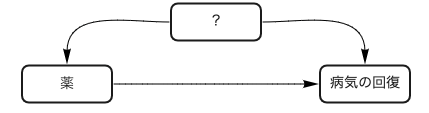
次に「血圧が、薬を飲むか否かと病気が回復するか」の共通原因だとします。

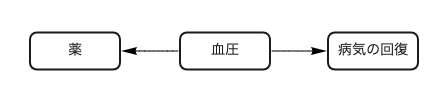
図３　Fork(分岐経路)の関係を示した因果ダイアグラム

この場合は調整すべきです。例えば「血圧が高い人ほど薬をちゃんと飲む」といった関係があるとします。そして薬の服用は血圧に影響がないとします。
すると血圧で調整しないと、薬と病気の回復との間に見せかけの相関関係（疑似相関）が生まれてしまいます。この共通原因の影響排除こそが交絡因子を調整する動機です。
今回のデータはRCTから得られているため血圧から薬への矢印はありません。しかし、現実には倫理的・費用的な面から今回の「薬」の箇所を直接介入できない場合も多々あります。例えば「喫煙と肺がんの関係」です。喫煙を直接介入できないため、肺がん患者のほとんどが喫煙者だとしても「喫煙遺伝子があると喫煙したくなり、肺がんにもなりやすくなる」といった未観測共通原因による疑似相関関係がデータに表れている、という主張が可能になり、実際にそれをタバコ会社がしていたそうです¹。

共通原因により両者が影響を受ける場合、薬と病気の回復の間に因果関係があったとしても、シンプソンズの逆転が発生する場合があります。例えば「血圧で調整するとどの条件でも薬は病気の回復に有益に見えるが、血圧で調整しないと薬は病気の回復に有害に見える」といったデータがえられる可能性があります。これは一見直感に反するためシンプソンズのパラドックスとも呼ばれています。血圧が共通原因の場合は調整をした方が正しいので、病気の回復には薬を飲んだ方が良いという結論になります。ただし、現実にはシンプソンズの逆転が起きるメカニズム（因果ダイアグラム）がわからないことも多く、その場合は部分の結果が全体の結果と一致のみに信じることにするPure-thing principal といった考え方もあります²。

ちなみに、血圧と性別の議論の違いは、「薬を飲むことにより性別は変わらない」から来ています。もし薬が原因で性別に影響がある場合は、血圧と同じように調整するかしないかは場合による、となります。
この関係性をPearl氏はFork（分岐経路）と呼んでいます。

最後に「薬が血圧の原因であり、病気の回復も血圧の原因である」といった状況を考えます。

図４　Collider（合流点）の関係を示した因果ダイアグラム

この場合は最初の例と逆で、調整すると薬と病気の回復に見せかけの相関関係が生まれてしまいます。
例えば、「薬を飲み、かつ病気が回復したら、血圧が下がる」といった場合に、「血圧が低い」で調整すると薬と病気の回復の関係に強い相関関係が生じますが、明らかにこれは見せかけの相関であって因果関係ではありません。
この調整（条件付け）をすると本来は独立な関係にも関わらず相関が生まれる（より一般的には情報が漏れてしまう）事象は、あまり直感的ではなく、しばしば混乱を生むそうです。その混乱の中でも一番有名な例はモンティ・ホール問題です。一流の統計学者とされる人ですら間違えたことから、旧来の統計学の欠点が垣間みえます。
この関係性をPearl氏はCollider（合流点）と呼んでいます。

任意の因果ダイアグラムはこの3種類の関係の連鎖で表現できます。

さて、こう書くとさほど難しい問題に見えませんが、連鎖経路では調整してはならず、分岐経路では調整すべきで、合流点では調整してはならない、といった簡潔な説明は因果革命以前にはなかったようです。私も大学入学後から今まで15年ほど統計学の講義やら実験計画やら実務でのデータ分析とそのレビューやらで、まぁまぁの学習・経験してきたはずですが、これほどまでに簡潔・明解な説明を受けた記憶がありません。10進法による小数点表示や繰り上がりの掛け算が発明されたことで小学校低学年の児童でも、中世ヨーロッパでは非常に困難とされた計算ができるようになったように³、統計的因果推論の概念と記述により人類のデータ分析力が格段に進歩した気がします。
私が因果革命が来ると感じている根拠その１です。

コラム：仮定した因果ダイアグラムの検証方法

上記では、この因果ダイアグラムが与えられたものとして議論しましたが、実際はどのように因果ダイアグラムを作成するのでしょうか？完全な因果ダイアグラム作成手順は発明されていないようですが、仮定が正しいかを検証する方法がいくつかあります。
基本的に「観測データ」から「それぞれが独立か否かを判定する」になります⁴。

XとYが独立な時

XとYの間に直接矢印がなく、XとYには連鎖経路や分岐経路の関係になるZもないことがわかります。

XとYは独立だが、Zで条件づけると従属する

XとYの間に共通結果Zがいます。つまり合流点の関係です。

XとYは従属だが、Zで条件づけると独立になる

XとYの間に直接の矢印はないが、連鎖経路や分岐経路の関係になるZがいることがわかります

XとYは独立だが、Zで条件づけると従属になる

XとYの間に直接の矢印はないが、合流点の関係になるZがいることがわかります

XとYには直接関係があるが、矢じるしの向きがわからない

一番手っ取り早いのはXに介入をし、Yが変化するか、あるいはその逆をみることです。
それが現実的でない場合でも、(1)XとYの関係が線形(2)その他の要因のXとYへの影響が非正規分布に従う、といった仮定ができる場合は矢じるしの向きを推定する手法が発明されています。この仮定はLiNGAMモデルと呼ばれます。
この手法の詳細は統計的因果探索｜講談社を参照していただくとして、ここではなぜ推定できるかを大雑把に解説します

方法1: 独立成分分析ベース

XとYの間が線形の関係なので、$Y=w_1 X$の様にか書けます。これをXとYの2つだけでなく因果ダイアグラム全体が線形の関係になっているとしたらXやYやZで記述していた観測地をまとめて $\vec{X}$ と表記し構造的因果モデル、$\vec{X}=W\vec{X}$ とかけます。ここでWは$\vec{X}$の長さの正方行列で、各要素は矢じるしの大きさに対応します。値が0の場合は矢じるしがない状態に対応します。ここで因果ダイアグラムの有効非循環グラフであるという仮定から、$W$は対角成分と上半分が0の三角行列でなければなりません。(私はここで「あーなるほどー」と感嘆の声が漏れました)。簡単にいえば、$\vec{X}$を独立成分分析にかけて、線形変換を施し仮定を満たす$W$を求めれば、矢じるしの向き（と大きさも）を求めることができます。

方法2: 回帰分析ベース

XからYを回帰分析したさいに、その誤差項は"XがYの原因ならば"Xと独立になります(Xに関係ないYへの直接原因への影響だけが残る)。逆に、"YがXの原因ならば"誤差項にXへの直接原因影響が残りXと独立になりません。(私はここで「なぁるほど！！」と膝を打って家族に不審がられました)。

無作為標本化実験ではない観察データからの介入効果の推定

Qiitaの読者層はWeb業界の方が多いと思うので、その方向けに書くと「A/Bテストしないでも介入効果がわかる」となります。「お前、 A/Bテスト実践ガイドではなんて訳したっけ？」と野次られそうですが、ここではその理由について書きます。

そもそもなぜ無作為標本化実験(RCT, A/Bテスト)が必要なのでしょうか？引き続き、薬と病気の回復を例にします。
病気の回復への薬の影響を調査したい、というのがRCT実施の動機とします。薬を飲むか飲まないかを無作為で割り当てます。

つまり $p(d,c)=p(c|d)p(d)$ の $p(c|d)$ が因果効果を示してくれれば良いのですが、薬と病気への回復にへの共通原因があると、うまく推測できません。極端な場合、本当の因果効果がなくても共通原因のせいで疑似相関が生まれ、観測データからの推定が$p(c|d) \neq p(c)$ になってしまうことが十分に起こり得ます。

図５　共通の原因があるときの因果ダイアグラム

因果ダイアグラムで書くとこうなります。実はRCTは因果ダイアグラムで書くと「？から薬への矢じるし」を削除する操作に対応します。

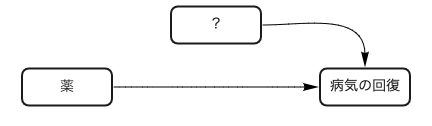
図６　共通の原因があるがRCTにより矢じるしが削除された因果ダイアグラム

なぜなら薬を飲むか飲まないかは無作為によって（強制的に）決まるので、本来あるはずの薬の原因と独立になってしまうからです。
RCTによる介入が因果ダイアグラム上の操作であり、従来の確率の記法が因果ダイアグラムの違いを区別できないため、Pearl氏は確率の世界に新たな記法を導入しました。これをdo-operator(do演算子)とよび、今回の例での薬への介入は $p(c|do(d))$ と表記されます。$p(c|do(d)) \neq p(c|d)$ です。

実際にデータ分析をするさいには、そのデータがどのような実験により得られたか（データの生成過程）を意識し、それにより分析手法を変えます。しかし、従来の確率の世界での表記上ではデータの生成過程の違いが反映されず、分析手法の決定（交絡因子の調整も含む）は半ば暗黙的に実施されてきた印象があります⁵。do演算子の追加により、確率の世界でデータ生成過程も扱えるようになり、どのような分析手法が正しいかを判断しやすくなるメリットは非常に大きいと感じています。私が因果革命が来ると感じている根拠その２です。

このdo演算子つきの確率を、それと等価なdoが無い数式に変換できれば従来の計算方法が利用できます。

Xの親たち(親の親の親の…も含む。家系図でいうところの先祖)を $pa$とし、各親を$pa_i$と表記すると

p(Y|do(X)) = \sum_i p(Y|X,pa_i)p(pa_i) 

平たく言うと「Xの全原因で調整して周辺化すればOK」です。RCTの場合は$p(Y|X,pa_i)p(pa_i)=p(Y,X,pa_i)p(pa_i)/p(X,pa_i)=p(Y,X,pa_i)p(pa_1)/p(X)p(pa_i)=p(Y,pa_i|X)$になり、$pa_i$ で周辺化されるため、$p(Y|do(X))=p(Y|X)$ になります。

しかしながら、そもそも「Xの潜在的なすべての原因paで調整」が現実的でないから、フィッシャーがRCTを発明しました。Xの原因には観測不可能な変数も大量にまざってそうです。統計的因果推論ではさらに踏み込んで介入効果を推定するために必要な変数のセットを判定する手法を開発しました。それはバックドア基準と名付けられています。これによりXの潜在的な親とXの関係性のすべてを記述できなくても介入効果が推定できるケースが格段に増えました。もちろん、任意の場合でRCTなしに介入効果が推定できるわけではありませんが、RCT以外の選択肢が増えたことで介入効果を推定できる事例が格段に増えることができました⁶。私が因果革命が来ると感じている根拠その３です。

バックドア基準以外にもフロントドア基準というものもあります。これはバックドア基準から導出できる基準ですが、多くの未観測共通原因を無視できる可能性があり、Pearl氏のお気に入りの基準だそうです。

図７　フロントドア基準を説明する因果ダイアグラム

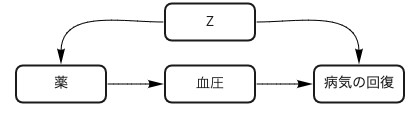
推定したい原因（上の図では薬）と結果（上の図では病気の回復）に共通原因（上の図ではZ）があったとしても、その間にZと独立な連鎖経路の関係がある要因（上の図では血圧）があり、因果の流れがその要因を必ず経由する場合は

$p(c|do(d=1))=\sum_b \Bigr( p(b|d=1) \sum_d p(Y|b,d)p(d) \Bigl)$

といったRCTを実施しなくてもZの影響を排除した介入効果の推定ができます。ただこの例だと、血圧が任意のZの結果になっていないと仮定しており、それははあまりに乱暴です。実際、今回の血圧に該当する要因の発見はかなり難しそうです。フロントドア基準の解説に統計的因果推論｜共立出版や入門　統計的因果推論｜朝倉書店では、タバコ（原因、薬に該当）、肺のタール蓄積量（血圧に該当）、肺がん（結果、病気の回復に該当）という例えでの人工データで解説していましたが、肺のタール蓄積量がZと影響しないと仮定するのは乱暴すぎだと突っ込みをうけていたことをThe Book Of Why｜Basic booksで明かしています。
ただ、The Book Of Why｜Basic booksでは、実データでRCTの結果とフロントドア基準で調整した観察データの因果効果量がかなり近しい値になった社会学の研究を紹介しています。この研究でもZと影響なしと論理的に示すのは厳しい（Zは観測不可なので実証も不可能）因子を使ってましたが、影響が少ない（無視できる）と仮定して計算を進めてみた結果、うまくいったと報告されています。

「but for~」などの司法で実際に使われる概念の定量化

実際の裁判などで、「もしhogehogeだったら犯罪的事象hugahugaは起きなかった、よってhogehogeを引き起こしたものは有罪」といった論理が用いられているそうです。実際に我々も日常的に似た論証を使っています。このような「実際は薬を飲んだけど、薬を飲まなかった場合に病気が回復する確率はどのくらいだっただろう？」といった問いの形式を従来の統計学の世界ではうまく扱えませんでした。このような形式での問題設定を反事実とおいてます⁷。

Pearl式の定式化では、反事実の操作は大まかに

1. 構造的因果モデルを作る
2. 実際の観測値を代入する
3. 「もし〜」の部分を強制的に値を書き換える（介入と同じ考え方）
4. 書き換える前後での変化を計算する

となります。
「なぜこれで反事実を扱っているとみなせるか」や「我々の素朴な論理たちはどのように定式化されるか」についての議論は、統計的因果推論｜共立出版をご参照ください。特に前者は哲学の世界で行われてきた議論と合流するため、Qiita上での簡易な説明は私には荷が重いです。後者は「強いAI」をつくるために必要だと思われ、その観点での解説はThe Book Of Why｜Basic booksの方をオススメします。Pearl氏の課題意識の原点はそこにあるとのことです。

「もしhogehogeだったらhugahugaである期待値」が正確に計算できれば、「何をどのくらいすべきか」といった行動計画を立案するさいの意思決定に極めて重要な情報提供ができます。これは、研究者だけでなく、病気の治療をしている医者や政策決定をする政治家の方やビジネス上の意思決定を迫られる起業家やサラリーマンといった現実世界で戦っている多くの人にとって有益な知見となり得ます。私が因果革命が来ると感じている根拠その４です。

因果革命がくるぞ！

さて、ここまで因果革命とは何かとその影響について簡単に書かせていただきました。まだ全然流行っていない言葉をなぜ私が推しているかという点を改めてまとめると

1. なぜそうすべきかの説明が困難だった「交絡因子の調整」が、概念が整理されることでだいぶわかりやすく明確になり、世の中のデータ分析力が大きく向上する
2. 実際の分析手法の選択に大きな影響を及ぼすにも関わらず数式上で表れなかったデータ生成過程（実験手続き）が数式に落とされ、何を暗黙的にしていたのかが、かなりわかりやすくなる
3. 無作為標本化実験（RCT、A/Bテスト）が実施できない状況下でも、現実的に介入効果の推定が可能な場合が大幅に増える
4. 我々の意思決定の考え方と近い状態で定式化されることで、意思決定に直接反映しやすい知見が得られる(もしくはAIが解決する)

となります。これらのためには、従来の統計学の定式化から概念上の飛躍が必要であり、これらの方法論を今までの計算の枠組みの中でTips的に用いることは少し難しそうです⁸。ですので、冒頭にあげた参考書、特にThe Book Of Why｜Basic booksでは統計的因果推論が必要な理由と今までなかった背景といった「なぜ」が書かれているため概念上の理解がしやすく、入門　統計的因果推論｜朝倉書店では数式上の操作が簡潔にまとまっているため、まずこれらを理解の羅針盤にすることをオススメします（逆に統計的因果推論｜共立出版を初手にすると数学の議論と哲学の議論の洪水に巻き込まれます。巻き込まれました。）

私の予想では、あと10年もすれば因果革命以前のデータ分析は非常に不便なものだと感じられ、「昔の人はよくこんなやり方でデータ分析してたな」と若者にネタにされているでしょう。

追記(2021/06/29)

なるほどです。少しわかった気がします
自分は今、Webサービス上でのデータを対象にすることが多く、全く観測できない交絡因子と因果関係に仮定を起きやすい観測値(種類も記述できる程度の量しかない)だけの世界を想定していた点にギャップがあるのかなと思いました(クローズドな世界に正にいます)

— oosugi naoya (@oosugi_naoya) June 28, 2021

統計的因果推論について、その素晴らしい点について煽りすぎた記事になっていため、その適用限界と注意点について補足します。

そもそも、因果ダイアグラムの仮定が妥当でない場合は、どんなに数式やバックドア基準をこねくり回したところで意味ある結論は導出できません。

因果ダイアグラムの仮定が妥当でない場合とは

1. 観測できない要因があまりに多すぎる
2. 因果関係の方向や存在について共通理解が乏しい
3. 扱いたい対象が複雑すぎて現実的に書き下すことが不可能

といった場合が考えられます。もちろん、独立性の確認により因果ダイアグラムの妥当性の確認や、バックドア基準などを用いることで上記の問題の軽減はできますが、銀の弾丸では決してありません。
上記のTwitterで引用させていただいた例では、経済データは妥当な因果ダイアグラムを仮定することが非常に困難な分野です（私は完全に門外漢ですが「そりゃ難しいだろうな〜」という感覚はわかります）。

とにかく注意しなければならない点は
「因果ダイアグラムを仮定した　ならば　因果関係を示せる」は間違った論理です。
他の多くの統計的分析手法と同じく、仮定が妥当でない場合はそこから得られる結論はナンセンスなものになります。

なんども強調しますが、統計的因果推論はすべての因果関係を明らかにできる魔法ではありません。

ここから個人的な見解ですが、下記のような状況が揃っている因果研究には妥当な場合が比較的多そうです。

1. すでに（暗黙的にでも）因果関係に仮定をおいている
2. RCTで部分的に因果効果を明確に推定できる
3. 関連する要素が高々数十未満の領域で、既存の因果関係をアップデートしたい

もちろん、この条件が揃っているからといって、統計的因果推論が適用可能かはわかりません。
The Book Of Why｜Basic booksでも書かれているように、因果ダイアグラムの仮定は、”マニュアル化されたルーチン”とは遠い作業になります。

私の学生時代に専攻した認知科学や、今の仕事のWebサービス内での行動分析などでは

1. 脳活動やらメンタルモデルやらのブラックボックスを扱い、暗黙的にも明示的にも因果関係を仮定していることが多い
2. RCTを用いた行動実験やA/Bテストなどで部分的な因果効果の検証を行いやすい
3. スキナー箱や一部機能の改修などで閉鎖的な環境が作れなくもない

と好条件が揃ってるため、統計的因果推論は実験室環境と現実世界の間のミッシングリンクを埋める一助になるのでは？と考えています

最後に

DAGはコミニュケーションツールとしてはとても役立つと思う。
そういう意味で使うことを躊躇しないで欲しい。

— Sato Shuntaro (@Shuntarooo3) June 28, 2021

因果関係について言及することをタブー視し暗黙的に仮定されるくらいだったら、不完全でいいので因果ダイアグラムを明示化して議論できたほうが１００００倍くらいマシだと思います。仮定のどこがおかしいかについて建設的な会話がしやすくなります ⁹。

1. 喫煙の肺がんへの因果効果についての歴史的議論については、統計学史の側面をThe Book Of Why｜Basic booksではまるまる１章割いています。また、がん‐4000年の歴史‐ 下では戦いの主要プレイヤーが医師、統計学者、弁護士、市民と移り変わる様が書かれておりこちらもオススメです。 ↩

2. A/Bテスト実践ガイドではここの記述がわかりにくく、私も訳注で補足したのですが、やっぱりわかりにくかったので、改めて補足します。A/Bテスト実践ガイドであった例では、「薬」が「A/Bテストの介入群」で、「血圧」が時間帯で、「病気の回復」が「コンバージョン」に対応します。もし、実験実施時の制約で「時間帯によってA/Bテストの割合を変更した」場合は、時間帯が両者の共通原因となり、シンプソンズのパラドックスが発声する可能性があります。この場合の正解は本記事で書かれているように「時間帯で調整する」になります。 ↩

3. 中世ヨーロッパのきっつい計算事情についてはあちこちで書かれていますが、自分はこの本でまず知ったのでそれを共有します。小数と対数の発見｜日本評論社 ↩

4. データからの独立性の判定はいくつかの計算方法が提案されています。お互いに正規分布の場合は独立ならば無相関になるのでわかりやすいのですが、そうでない場合は相関係数による判定はできません。与えられた非正規分布同士の独立性の判定基準は独立成分分析の分野で発展しています。そこではネゲントロピーやら高次キュムラントやらを基準としております。 ↩

5. 私は学部では認知科学を専攻し、そこでは統制のとれた実験からの適切な統計処理（主に仮説検定）が重要視されていました。あくまで私見ですが、その実験計画から適切な統計処理の決定までのフローがArtと化している様に感じ、データ分析には経験が必要だと考えていました。また、民間の営利企業での実務でデータ分析のレビューを受ける/実施することも多く、そのさいに相関分析で何を仮定としているかもっと明確にしてほしいと思うことが多かったです。今では、因果関係を確率の世界で適切に扱えなかったことがこれらの「気持ち悪さ」の主要な要因であると思うようになりました。因果革命後の世界では因果的過程の明示化とそれに応じた適切な代数的操作によって語られる、より明確かつ再現性の高い世界が訪れると確信しています ↩

6. 所属する会社での業務で実施したため、内容の公開はできませんが、RCTができない条件下の実データで介入効果を推定し、かなり信頼できそうな結果が得られた経験があり、私はこの威力を実感しています。具体的な応用例はThe Book Of Why｜Basic booksにも書かれているので、興味ある方は是非ご覧ください。 ↩

7. 反事実といえば、欠損値補完の統計手法をベースとしたルービン因果モデルが有名です。しかし、Pearl氏の定式化ではルービン因果モデルは従来の関連（association）の方法論に閉じているため、因果のはしごの方法論的に上位に位置づけられる反事実（と介入も）の問題を解くことはできないとされています。この議論は統計的因果推論｜共立出版では避けられているようにも見えますが（様々な因果に関する哲学的な考え方との比較を実施しているにも関わらず触れられていないため）、The Book Of Why｜Basic booksでは直接言及されています。 ↩

8. 最近はcausalgraphicalmodelsや、DoWhyといったPearl流の統計的因果推論を実行するための計算ツールも出ていますが、このツールを活用するためには自己の概念からアップデートしないと難しいのでは、というのが私の感想です ↩

9. やはり個人的な感想ですが「介入効果の推定の話がしたいのに、因果関係を仮定せず同時確率の数字だけを持ってくるんじゃねぇ」というのを会話しなくて済むようになるだけで、非常にありがたい話です。 ↩