音とFM音源の軽い紹介と今昔物語

自分がハマり、今も楽しんでいる FM音源 の面白さ、奥深さについて紹介します。
プログラミングは抜きにして、音の成り立ちからFM音源の原理、実例を書いてみました。

そもそも音とは

空気中を伝播する微弱な圧力変化の波動を「音」と呼びます。
真空中など、伝播する物質の無い場所に音は伝わりません。

普段我々が耳にする音によって生じる気圧変化は μPa から Pa 程度の範囲であり、
天気予報で耳にする 1,013hPa という大気圧と比較して非常に微弱な変化です。
$(※μ=10^{-6},　h=10^2)$

低気圧や高気圧によって外気圧は常に変化します。
しかし、その変化を我々は耳で聞くことはできません。

音に比べれば十分に巨大な変化であるはずの気圧の変化を感知できないのは、
変化の速さが極端に低いことが原因です。

音と周波数

音は波の性質を持ちます。
波の押し引きの速さは 周波数 (単位: Hz) で表し、1秒間に1回の押し引きがあるときに 1 Hz と表現します。
実際の音は、様々な周波数の波が合成されてできています。（関連: 重ね合わせの原理）

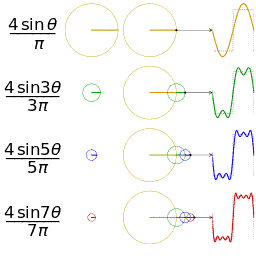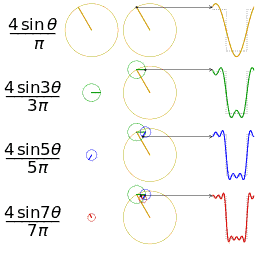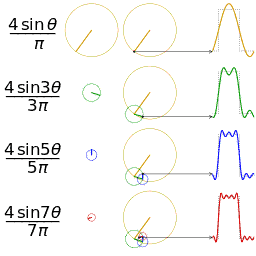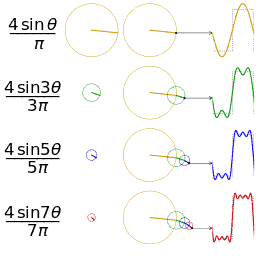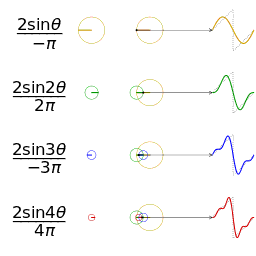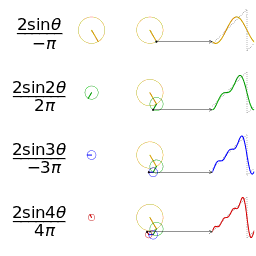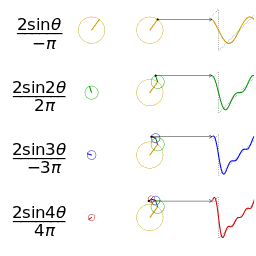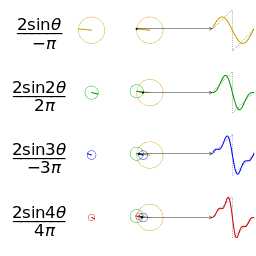__矩形波__に対応する針の動き	__鋸歯波__に対応する針の動き

一つの波を表現したいとき、逆向きに進む時計の針の進み方で例えると理解がしやすいです。
波の押し引き1回分を、時計の針1周分と表現します。

針が進むと角度が $0° → 90° → 180° → 270° → 360°$ と変化します。
$360° = 0°$ ですから、これで押し引き1回分と考えます。

現実的には、波の表現には正弦関数（サイン関数）を用い、角度はラジアン法を用います。
ラジアン法により $0° = 0 \text{ rad}$、 $180° = \pi \text{ rad}$、 $360° = 2\pi \text{ rad}$ とそれぞれ表現されます。

波が押し引き1回分で $2\pi$、2回分で $4\pi$、 $f$ 回分で $2\pi f$ です。
これが1秒後なら $2\pi f$、2秒後なら $4\pi f$、$t$ 秒後なら $2\pi ft$です。

これを正弦関数に当てはめると、一つの周波数の波の式が完成します¹。

x(t) = A\sin2\pi ft

正弦波のプロット (アニメーション)

アニメーションのリンク先では、実際に針が動く様子が観察できます。

ここで $A$ は波形の振れ幅、音の大きさを表すパラメータです。
ところで、時計の針がどの角度にあるかを表す $2\pi ft$ の部分は 位相 と呼ばれます。

「機械的」な音の発生

1983年、任天堂によってファミリーコンピューターが発売されました。
リコー製 2A03 と呼ばれるCPU内部に、いわゆるピコピコ音を鳴らすための音源が内蔵されていました。

pAPU と呼ばれる音源ユニットは、矩形波、擬似三角波、ノイズ、DPCM といった多様な波形を生成することができました。
これらは今日私たちが耳にしている PCM と呼ばれる音源と比べ、より「機械的」、幾何的な波形を生成します。

参考: 2A03で作られた作品例 (他者作品)
Everlasting Saturday (2A03 chiptune) - https://www.youtube.com/watch?v=n3nzb_xDm34

耳で聞こえた通りのリアルな音を再現できる PCM と比べ、「機械的」な音源の利点は、発音に必要なデータの大きさがはるかに少量で済む点です。
PCM で CD の音質ならば1分で約10MBも消費する一方、pAPU であればどんなに大きくても 数百バイトから数KB程度です。

pAPUはその後、ゲームボーイ、ゲームボーイアドバイスに採用され、現在ではこれを再現できるフリーウェアも多数存在します。

FM音源

pAPUよりも遥かに多彩な音の表現を可能にしたのが、メガドライブやMSX、PC98の拡張音源などに搭載された、FM音源です。

FM とは、周波数変調 (Frequency Modulation) の略で、先ほど説明した時計の針の進む速度を周期的に加減速させて「機械的」な波形を生成する手法です。
この原理は、FMラジオ放送でも応用されています。

先ほどの式、

x(t) = A\sin2\pi ft

の位相部分を周期的に変化させると以下の式ができます。

x(t) = A\sin(2\pi f_ct + \beta\sin2\pi f_mt)

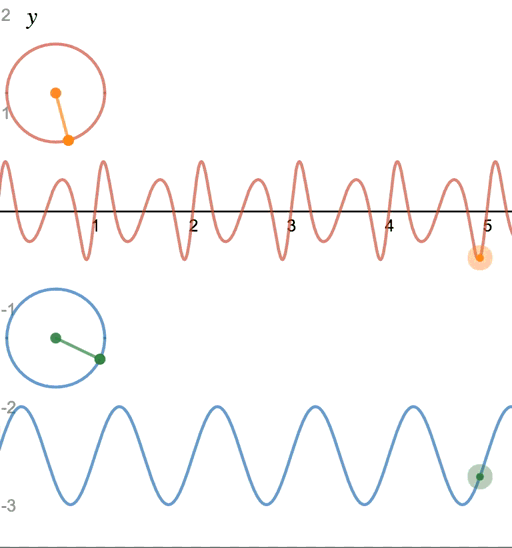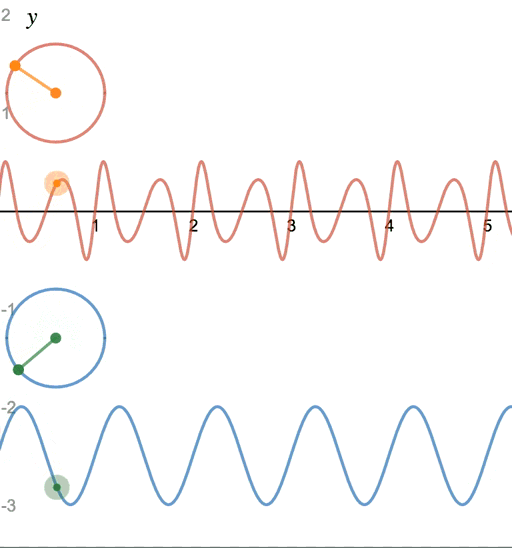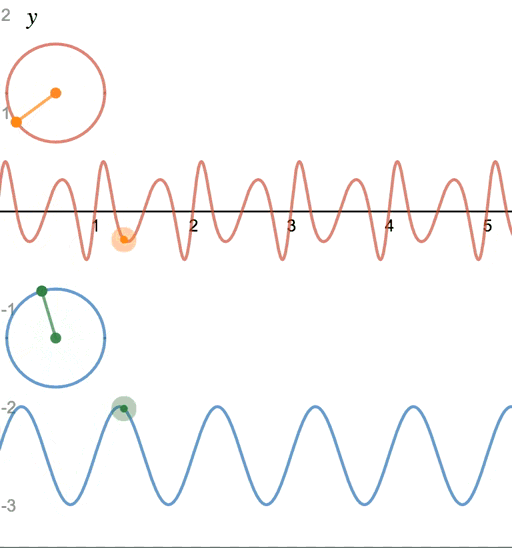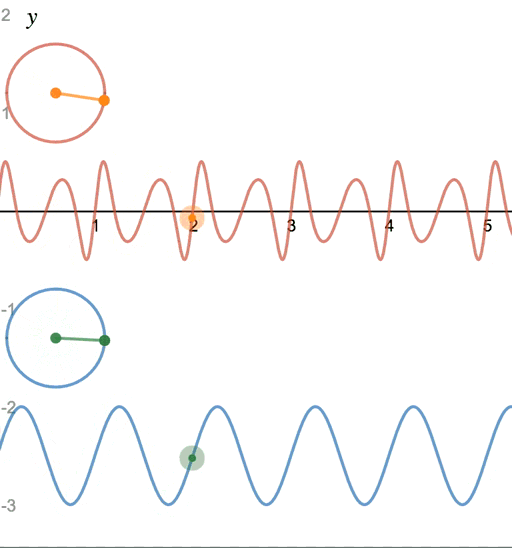上: FM音源、下: 正弦波 (アニメーション)

$\beta\sin2\pi f_mt$ の部分が新たに加わりました。これがFM音源の波形の式です。
よく見ると、正弦関数の中に別の正弦関数が入っているように見えます。

$\beta$ は 変調指数、$f_m$ は モジュレータ周波数 と呼ばれます。
$\beta$ が大きいほど音の歪みが強くなります。

時計の針が早く進んだり、逆行する様子が周期的に繰り返されるのが、FM音源の特徴です。
アニメーションをぜひ開いて、パラメータを操作してみてください。

FM音源は先ほどのpAPUとは原理的に発生方法が異なり、ピコピコ音とはまた異なった音となります。
しばしば金属的、「みょーーん」といった擬音語で表現されます。

参考: FM音源で作られた作品例 (他者作品)
[Original Song] Happiness Awaits - https://soundcloud.com/pedipanol/happiness-awaits

さらにFM音源発生器を直列に繋げることで、複雑な倍音、ノイズを生成できます。
一つのFM音源発生器は オペレータ と呼ばれ、オペレータの組み合わせを アルゴリズム と呼びます。

すごいぞヤマハ

秋葉原のガチャガチャで手に入れた、YM2608 (下)

1985年にヤマハによって開発され、PC98シリーズの拡張音源として搭載された YM2608 は、pAPU を凌ぐ音源性能を持っていました。

ステレオFM音源6チャネル (1チャネルにつき4オペレータ)、矩形波3チャネル、リズム音源6チャネル、DPCMの合計16チャネルを同時に発音できる性能を持っています。

さらに特徴的なのが、YM2608 はデジタル処理によってFM音源を生成していることです (矩形波を除く)。

YM2203 をブレッドボード上にて動作させているところ

いわゆる YM シリーズは多岐に渡り、ゲーム機のみならず一般のPCにも搭載されていた時期がありました。
外部にRAM、DACなどの周辺ICは必要であるものの、これらのICは 5V で駆動ができ、LSIさえ入手できればブレッドボードに載せて発音が可能です。

FM音源伝説 - 何が出るかはお楽しみ！	キットを購入、はんだ付けしてPCと接続

私は、秋葉原にある FM音源伝説 というガチャガチャで YM2203 を入手したことに始まり、PCからMIDIを演奏させるためのソフトウェアをC#で書いていたり、ブレッドボードから半田付けが必要なユニバーサル基板上で動作するキットを購入して音を楽しんだり... といった用途で使っています。

30年以上前のLSIとはいえ、生成される音は今も色褪せません。

日常の中のFM音源

90年代後半からストレージサイズの増大、CPU の性能向上、MP3 などの圧縮技術の進歩もあり、PCM の問題点であった容量の問題は解決されました。
MIDI は FM音源からサンプリング音源になり、携帯電話に搭載されていたFM音源も次第に姿を消し、今ではほぼ全ての音源が PCM になったと言っても過言ではありません。

しかし、FM音源は今でも私たちの生活の中で生きています。

例えば、JR の発車メロディ、実はFM音源です。

最後に。

どんなにハイレゾが普及しても、FM音源の音は FM音源にしか作れません²。
シミュレータなどによりゲーム機搭載の FM音源を真似ることはできますが、実機の音とは似て非なるものです。

IC/LSIを入手して、データシートを読んで、部品を組み立て、プログラムを書いて...
やっと鳴った瞬間、自分だけの音を手に入れたという喜びを得るのです。

---

注: 引用物の出典は画像の title に示しました。

1. 実際は初期位相など他のパラメータも登場しますが、ここでは最も単純な式を示しました。 ↩

2. 実機から録音した場合を除きます。 ↩