STM32F303K8でリアルタイム波形合成と出力

前回は STM32F303K8 の DAC を使って正弦波を出力 させました。バッファ上のデータは変更せず、出力周波数はサンプリング周波数に依存していました。

今回は他の波形や任意の周波数をリアルタイムに波形合成、出力を考えます。

やりたいこと

• STM32F303K8 で DMA を介して DAC から出力する
• リアルタイムに任意周波数の波形を合成する
• オーディオ出力としてその波形を収録する

前提として NUCLEO-F303K8 を使い、PLL によるシステムクロックを 64 MHz に引き上げて使います。

バッファリング

F303K8 は FPU を搭載していますが、fast_math.h の sinf 関数はリアルタイム波形合成に使えるほど高速ではありません。システムクロックを 64 MHz に引き上げてもサンプリング周波数が 2 kHz 程度の速さしか達成できません。

そこで今回は sinf 関数をリアルタイムの波形合成に直接使わず、LUT を使った方法で種々の波形を合成させます。

LUT

計算に時間のかかる値をあらかじめ計算しておき、配列に格納します。値を使うときは位相から配列のインデクスを求め、配列から値を取得します。これを LUT (Lookup Table) と呼びます。値の精度は配列の長さとその補完方法に依存します。

配列に格納する値は実数値である必要はありませんが、インデクスは整数でなくてはならないため、位相をどう整数で表すかが鍵となります。今回は高速化を優先するため、正弦波の位相を uint32_t で表し、配列の長さを 2の冪 にします。同様の理由で、LUT に格納する正弦波は 1周期 とします。

正確には、位相と配列長は 2の冪 にする必要はありません。ただし 2の冪 以外の値を使う場合は位相値のクランプや実数演算、余剰演算が必要になります。

以下に正弦波の LUT の実装を示します。

lookup_sin

# include "fastmath.h"

# define BV(x) (1 << (x))
# define PI 3.141592654

# define LUT_BIT 10
# define LUT_SIZE BV(LUT_BIT)
# define LUT_PHASE(x) ((x) / BV(32 - LUT_BIT))

int16_t lut_sine[LUT_SIZE] = { 0 };

int32_t lookup_sin(uint32_t phase) {
  return lut_sine[LUT_PHASE(phase)];
}

void initialize() {
  for (uint32_t i = 0; i < LUT_SIZE; i++) {
    lut_sine[i] = (int16_t)(sinf(i * 2.0 * PI / LUT_SIZE) * (BV(16 - 1) - 1));
  }
}

int main(void) {
  ...
  initialize();
  ...
}

マクロ BV(x) は 2の冪 を表します。 BV(10) で 1024 です。

マクロ LUT_PHASE(x) は uint32_t の位相を LUT の位相（インデクス）に変換します。32 ビットから 10 ビットへの除算となり、コンパイルすると 22 ビットの右シフトになります。

配列 lut_sine[LUT_SIZE] は const にしません。初期化の時間コストはかかりますが、実行時に RAM から LUT を予め展開したほうが 20% ほど高速です。

LUT は int16_t ですが、高速化を狙って関数 lookup_sin の返却値は int32_t にしました。

出力周波数の計算

関数 lookup_sin(uint32_t phase) の引数に与える位相を計算します。

位相を uint32_t の範囲で与えるため、最小値は $0$、最大値は $2^{32} - 1$ です。正弦波の 1周期 を転送するのにサンプリング周波数の逆数 $\frac{1}{f_s}$ [s] かかるので、$f$ [Hz] の正弦波を出力するのに必要な1サンプルあたりの位相の増分 $\Delta\theta$ は、

$\Delta\theta = \frac{2^{32}}{f_s} \cdot f$

と計算できます。サンプリング周波数 $f_s$ [Hz] は固定とすると、$\frac{2^{32}}{f_s}$ の部分は定数となり、$f$ と乗算すれば $\Delta\theta$ がすぐに求まります。

以下に正弦波のデータをリアルタイムに生成するコードを示します。

# define DAC_BIT 12
# define VALUE_VU12(x) ((x) / (BV(16 - 1) / BV(DAC_BIT - 2)) + BV(DAC_BIT - 1))
# define BUFFER_SIZE BV(10)

uint16_t buffer[BUFFER_SIZE] = { 0 };

const float sampling_frequency = 48.0e3;
const float phase_factor       = 4294967296.0 / sampling_frequency;
float frequency                = 1000.0;

uint32_t phase       = 0;
uint32_t delta_phase = (uint32_t)round(phase_factor * frequency);

void fill_buffer(uint32_t start, uint32_t end) {
  for (uint32_t i = start; i < end; i++) {
    buffer[i] = VALUE_VU12(lookup_sin(phase));
    phase += delta_phase;
  }
}

マクロ VALUE_VU12(x) は 32 ビット整数の出力を DAC 出力に合わせて 12 ビット整数に変換します。

変数 frequency で周波数を変更できます。実行中に変更した場合は変数 delta_phase を再計算してください。

DMA 割り込み

DMA が RAM から DAC への転送を完了させると、関数 HAL_DAC_ConvCpltCallbackCh1 が実行されます。この関数は __weak が付与されているため、ユーザ側で上書きできます。

しかし、割り込みが発生してもなお DMA の転送は停止せず、バッファの冒頭にある古いデータを DAC に転送し始めます。つまり、波形合成中のデータを DAC に送ってしまうため波形が崩れてしまいます。

実は DMA 割り込みにはもう一つ、関数 HAL_DAC_ConvHalfCpltCallbackCh1 が存在します。この関数はバッファの半分の転送が終わったら実行されます。つまり同じバッファを2分して、ダブルバッファリングが可能になります。

DMA での転送が開始して前半の転送が終わると、関数 HAL_DAC_ConvHalfCpltCallbackCh1 が呼び出されます。後半データの転送中に、関数内で前半データの生成を行います。後半データの転送が終わると 関数 HAL_DAC_ConvCpltCallbackCh1 が呼び出されるので、前半データの転送中に、後半データの生成を行います。こうすることで、切れ目のないデータをリアルタイムに DAC に転送できます。

# include "stm32f3xx_hal.h"

// 前半データ転送終了
void HAL_DAC_ConvHalfCpltCallbackCh1(DAC_HandleTypeDef *hdac) {
  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_RESET);
  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_3, GPIO_PIN_SET);

  // 前半データ生成
  fill_buffer(0, BUFFER_SIZE / 2);

  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_3, GPIO_PIN_RESET);
}

// 後半データ転送終了
void HAL_DAC_ConvCpltCallbackCh1(DAC_HandleTypeDef *hdac) {
  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_SET);
  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_3, GPIO_PIN_SET);

  // 後半データ生成
  fill_buffer(BUFFER_SIZE / 2, BUFFER_SIZE);

  HAL_GPIO_WritePin(GPIOB, GPIO_PIN_3, GPIO_PIN_RESET);
}

今回は DMA 割り込みがされるごとに GPIO_PIN_4 を反転、データ生成中は GPIO_PIN_3 に H を出力して波形合成の負荷率を計測します。

実装

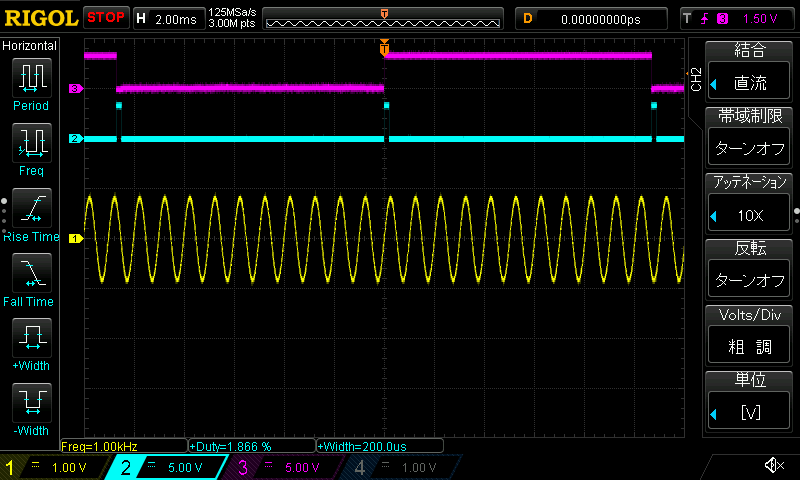
実行すると、1 kHz の正弦波が PA4 （A3） ピンから、負荷率を表す信号が PB13 (D13) ピンから、DMA の割り込みを表す信号が PB4 (D12) から出力されます。

黄色(ch1)が正弦波出力、水色(ch2)が負荷率、紫色(ch3)が DMA 割り込みです。

サンプリング周波数は 48 kHz、バッファサイズは 1024 なので、10.67 ms の余裕があります。正しく 1 kHz の正弦波が出力され、負荷率は 1.9%、時間にして 200 μs となりました。

正弦波以外の波形を作る

LUT に入れる波形を変えれば、正弦波以外の波形を作れます。配列名 lut_sine からは変わるので、本来ならば別の名前を使うべきですが、今回はこのまま使います。

sine_wave

void initialize() {
  for (uint32_t i = 0; i < LUT_SIZE; i++) {
    lut_sine[i] = (int16_t)(sinf(i * 2.0 * PI / LUT_SIZE) * (BV(16 - 1) - 1));
  }
}

矩形波、三角波、鋸歯波を作ります。

square_wave

void initialize() {
  for (uint32_t i = 0; i < LUT_SIZE; i++) {
    lut_sine[i] = (int16_t)((i < LUT_SIZE / 2 ? 1 : -1) * (BV(16 - 1) - 1));
  }
}

triangle_wave

void initialize() {
  for (uint32_t i = 0; i < LUT_SIZE; i++) {
    lut_sine[i] = (int16_t)((i < LUT_SIZE / 4 ? i :
                             i < (LUT_SIZE / 4) * 3 ? LUT_SIZE / 2 - i :
                                                      i - LUT_SIZE)
                            * (BV(16 - LUT_BIT + 1) - 1));
  }
}

sawtooth_wave

void initialize() {
  for (uint32_t i = 0; i < LUT_SIZE; i++) {
    lut_sine[i] = (int16_t)((i < LUT_SIZE / 2 ? i : i - LUT_SIZE) * (BV(16 - LUT_BIT) - 1));
  }
}

出力される波形を以下に示します。

波形	矩形波	三角波	鋸歯波
出力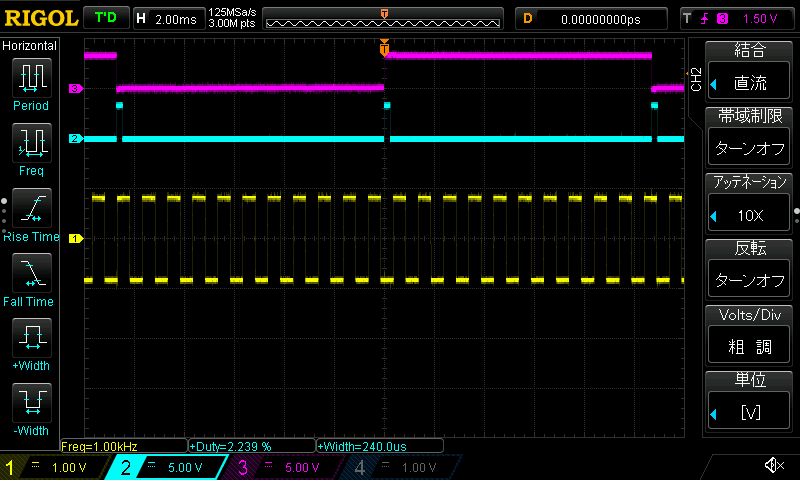
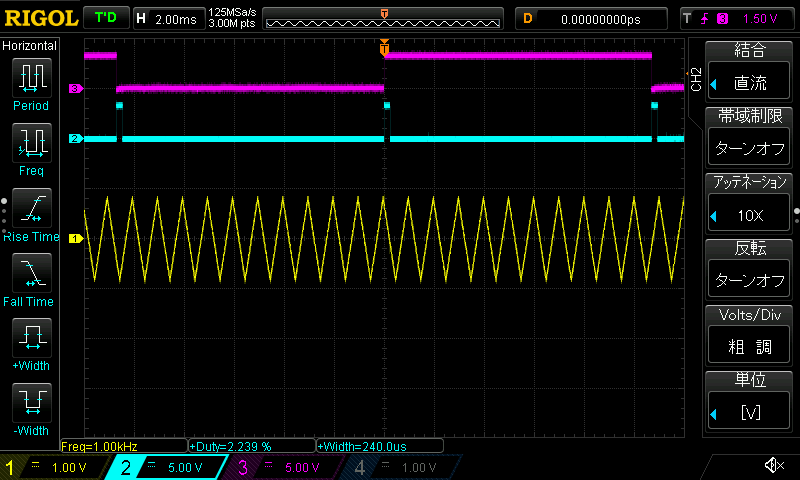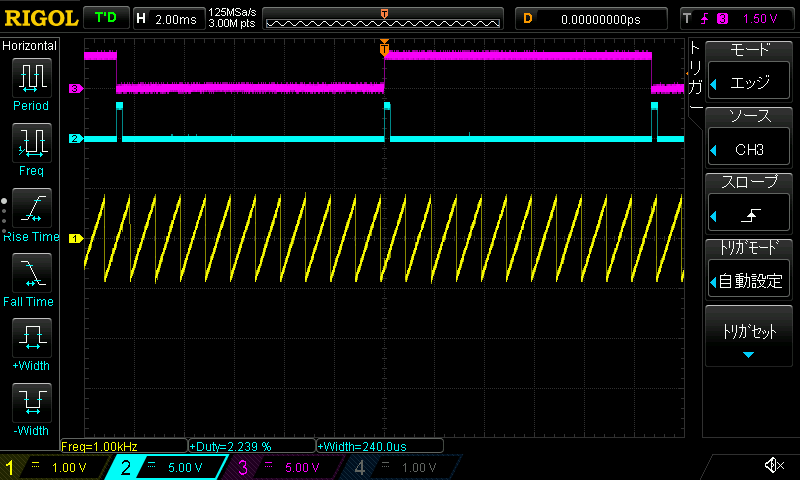負荷率	2.2%	2.2%	2.2%

若干の負荷の上昇がありますが、正しく各波形が出力されました。

回路図

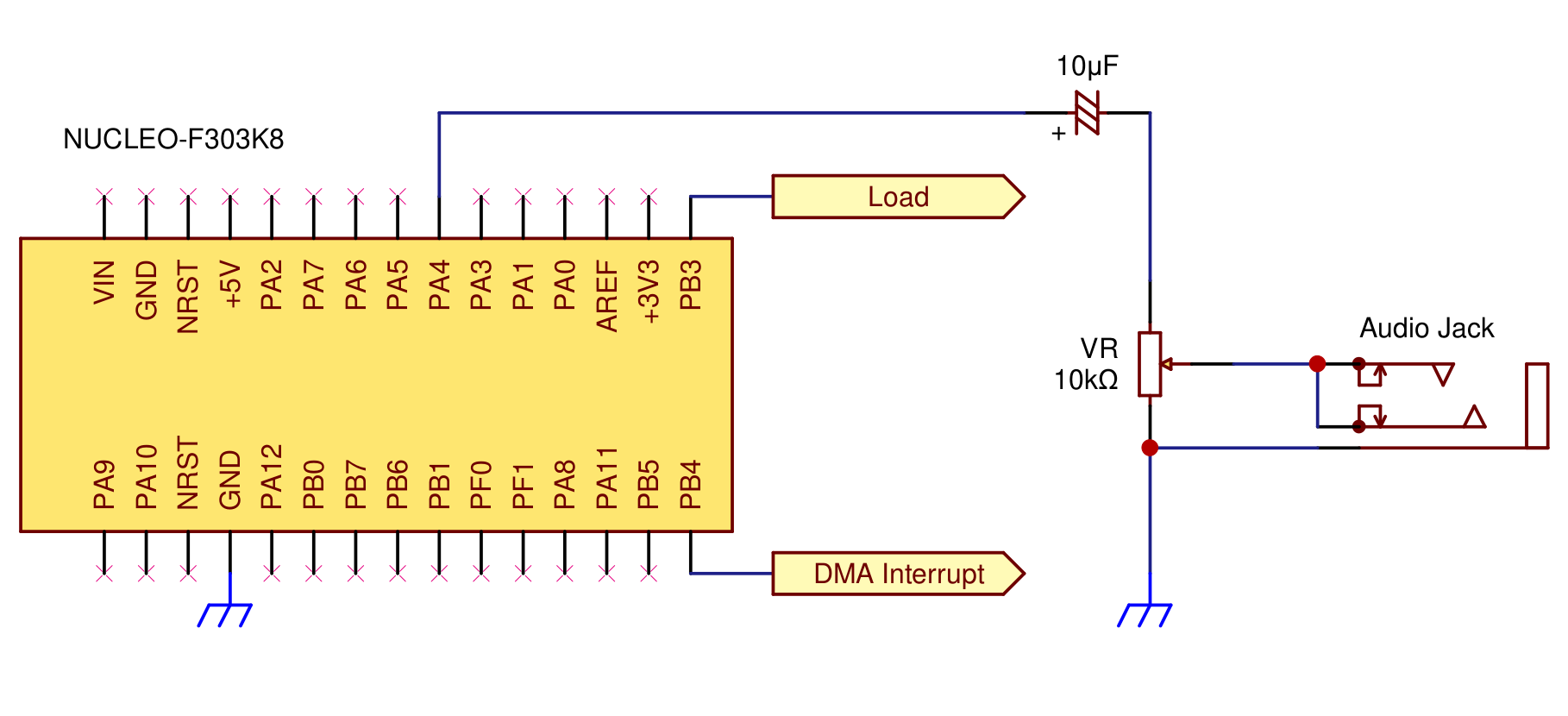
最後に、DAC から出力された波形を音声として収録するために今回使った回路を示します。

収録用 PC に直接繋いでいるため、追加のオペアンプなどはありません。しかしイヤホンなどで駆動させる場合は適宜出力を減衰させ、オペアンプでインピーダンスを下げる必要があります。

回路図

参考資料

• miniDDSとテーブル補間
  
  http://elm-chan.org/junk/mdds_ipol/report_j.html