🀄四川省🀄
四川省、とは、平面に並べられた麻雀牌から
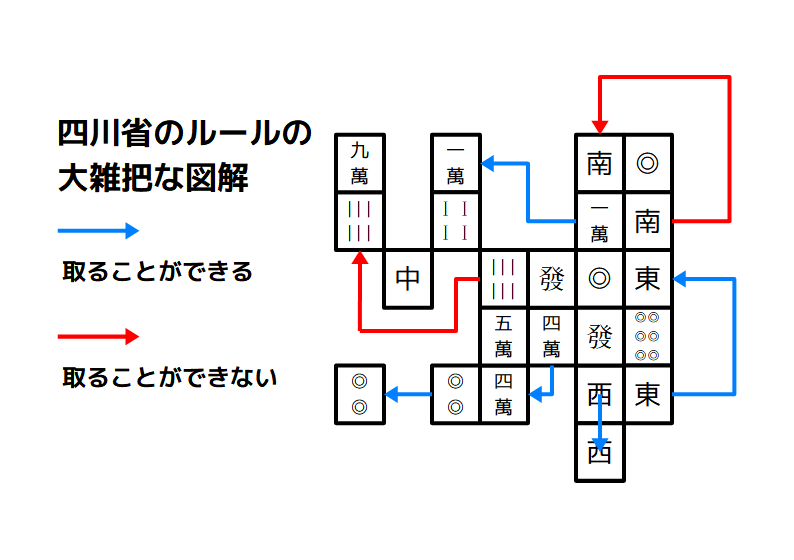
- 軸に沿った三本以内の連続した線分で結ぶことのできる同じ柄の牌
を取り除いて行き、すべてを取り除いたらクリアというパズルゲームです。
基本的には8行17列(136枚=数牌+字牌)ですが、難易度設定ができるものだと多かったり少なかったりすることもあるようです。
線分の間に、別な牌が在ってはいけません。
隣り合っているのはOKです。
「線分が三本以内」は、言い換えれば「角が二つまで」ですから、『二角取り』と呼ばれることもあるようです。
プログラムとしては、そんなに難しい類のものではないのですが、Qiita に実装例が無い(見つけられてないだけ?)ようなのでざっくり解説した後に実装例の紹介をしたいと思います。
とりあえず遊んでみよう
というわけで CodePen。
柄は適当ですがご容赦ください。
See the Pen ShisenShoProto by nagtkk (@nagtkk) on CodePen.
- マウスクリックで選択
- 全部消せたら clear
- これ以上取ることができない状態(詰み)になったら game over と表示されます。
- 生成時に詰みチェックしているので、手順を間違えなければ解けるはず。
※ Edge で動かない、という話があったのでコードをやや修正。Babel が Spread Properties を変換してくれないらしい。
取ることができるかどうかの判定
取ることができる牌の組は、
- 軸に沿った三本以内の連続した線分で結ぶことのできる同じ柄の牌
でした。
「同じ柄の牌」の部分は、簡単なんで割愛。柄IDでも振っておけば良し。
少し考える必要があるのは「軸に沿った三本以内の連続した線分で結ぶことのできる」の部分。
とある牌からもう一方の牌への経路だと考えれば、閉じた二次元平面ですから、
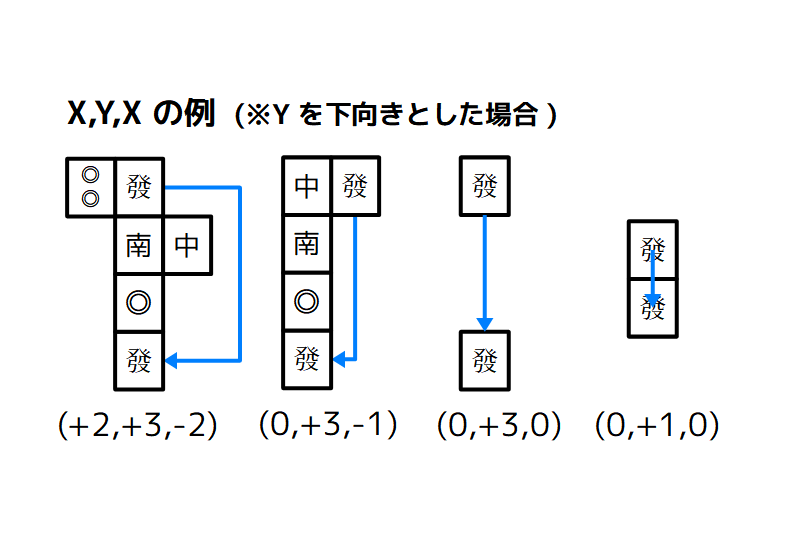
- X 方向に
i移動して、Y 方向にj移動して、X 方向にk移動 - Y 方向に
i移動して、X 方向にj移動して、Y 方向にk移動
のどちらかにしかなりません。
線分 2 本や線分 1 本、隣り合っている場合も、i,k に 0 が入っていると思えば、結局はこの条件に合致します。
というわけで、XYX と YXY のどちらかの条件に合致する経路を見つけ出す、というのが判定アルゴリズムの本体となります。
一般的な経路探索アルゴリズムを使って、出てきた経路が条件を満たしているか判定する...としてもよいのですが、牛刀割鶏に過ぎますから、ここでは四川省用のルーチンを考えます。
四川省用の経路探索
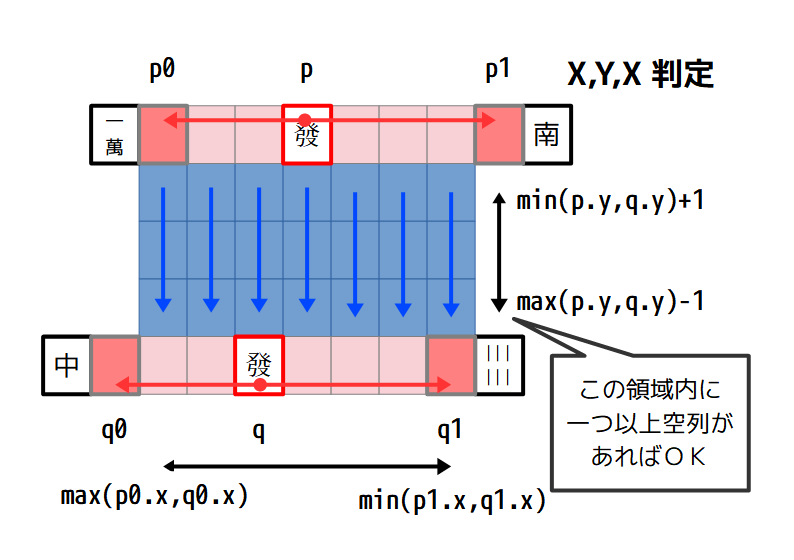
四川省用の経路探索を簡単に図示すれば、以下のようになります。
一つ目の牌の座標を p 、もう一つを q とします。
経路が XYX であった場合、最初と最後の X 方向の移動は、それぞれ p の行と q の行での移動になります。
というわけでまず、p と q の左右にどれだけ空きがあるか調べて、最も左側を p0,q0 右側を p1,q1 とします。
あとは p0-p1 と q0-q1 の X 軸方向の重複領域について、その間に一本でも縦の線を引くことができれば、つまり、空列(すべて空の列)が一つでもあれば、経路が見つかったと言うことになります。
経路が YXY の場合についても、縦横入れ替えて同じことをするだけなので省略。
理屈自体はとても単純。
JavaScript での実装例
さて、実際にゲームを作るには、これを実装すればいいわけです。
そこそこ長いのでもう作れるぜって人は、すっとばしてください。
そのまま作っても面白くないので、今回は XYX の判定と YXY の判定を共通化してみます。
言語は JavaScript で。
Qiita には解説たくさんあるからきっと大丈夫。たぶん。
一応、応用しやすいように、外部ライブラリ等使わずに作っていきます。
全実装は CodePen からどうぞ。
まずは下準備。
const { min, max, floor, ceil, random } = Math;
const pick = a => a.splice(a.length * random(), 1)[0];
const range = (start, stop, step) => {
if (stop === undefined) {
stop = start;
start = 0;
}
step = step || (stop < start ? -1 : 1);
const length = max(0, ceil((stop - start) / step));
return Array.from({ length }, (_, i) => start + step * i);
};
pick は、配列からランダムに一要素抜き取る関数です。
range は、Python の range と似たようなものですね。
指定範囲の数値が入った配列を作成します。
次は座標系。
まずは定数から。
const N = 17 * 8;
const W = 17 + 4;
const H = 8 + 4;
N は牌の数です。今回はオーソドックスに 17*8。
W と H は盤面の横幅と縦幅です。
周辺に空白と壁を設けるため、それぞれ +4 しています。
const X = p => p % W;
const Y = p => floor(p / W);
const fromXY = (x, y) => x + y * W;
const fromYX = (y, x) => fromXY(x, y);
XY座標と配列のインデックスの変換です。
fromXY だけじゃなくて fromYX を用意しているあたりがミソ。
基本的に座標はインデックスのまま扱います。
それでは盤面を作ります。
const create = () => {
const tiles = range(N).map(i => 1 + floor(i / 4));
const board = range(W * H).map(p => {
const d = min(X(p), Y(p), W - 1 - X(p), H - 1 - Y(p));
return d === 0 ? -1 : d === 1 ? 0 : pick(tiles);
});
return { board, target: -1, rest: N };
};
各麻雀牌は 1 以上の整数、空きは 0、壁は -1 として、盤面を作成しています。
麻雀牌は一度配列 tiles に連番で突っ込みます。
同じ柄の牌は各 4 枚あるので対応する整数は 1+floor(i/4)。
そこから pick でランダムに取り出しています。
ゲーム状態は盤面として扱う配列 board のほか、target (選択中のインデックス, 未選択は-1) と rest (残りの牌の数)を準備。
次はゲーム状態の更新。
クリック等で指定された座標 p を入力として状態を更新します。
const update = (state, p) => {
const { board, target, rest } = state;
if (board[p] <= 0) return state;
if (target < 0) return { ...state, target: p };
if (!test(board, target, p)) return { ...state, target: -1 };
return {
board: board.map((v, i) => i === p || i === target ? 0 : v),
target: -1,
rest: rest - 2
};
};
ゲーム状態は書き換えずに、新しいものを作って返却。
壁や空白なら何もせず。
未選択状態なら、与えられた座標を選択状態にします。
既に選択済みの牌(target)があるなら、後述の判定用関数 test で p と target の組を取り除くことができるかをチェックします。
判定に失敗したら単に未選択状態にし、成功したら、牌の組を空白に置き換え、残りの数を 2 減らしてから未選択状態にします。
さて、ここから判定ルーチン。
const move = (board, p, d) => board[p + d] ? p : move(board, p + d, d);
const pass = (board, p, q, U, V, C) => {
const e = C(1, 0);
const u0 = max(U(move(board, p, -e)), U(move(board, q, -e)));
const u1 = min(U(move(board, p, +e)), U(move(board, q, +e)));
const v0 = min(V(p), V(q)) + 1;
const v1 = max(V(p), V(q)) - 1;
const us = range(u0, u1 + 1, 1);
const vs = range(v0, v1 + 1, 1);
return us.some(u => vs.every(v => board[C(u, v)] === 0));
};
const test = (board, p, q) =>
p !== q && board[p] === board[q] && (
pass(board, p, q, X, Y, fromXY) ||
pass(board, p, q, Y, X, fromYX)
);
move は、盤面 board 上の座標 p を空白が続く限り d ずつ移動する関数です。
図解での左右に見ていく部分。
そして pass が今回記事に書いた経路判定。
経路そのものではなく、経路があったかどうかのみを返すので pass に。
引数として盤面 board と二つの座標 p,q に加えて、XYX または YXY の、
- 1つ目(=3つ目)の軸の値を得る関数
U - 2つ目の軸の値を得る関数
V - 各軸の値からインデックスを得る関数
C
を与えることで両対応にしています。
u → x, v → y と読み替えれば、解説で図示しているものと、おおよそ一致していることが確認可能かと思います。
pass 内、e は一つ目の軸の単位ベクトル相当で、
p,q から -e と +e に向かって空白を探します。
一つ目の軸の探索範囲は u0 から u1 まで。
二つ目の軸の探索範囲は v0 から v1 まで。
領域内の判定は配列使って書いちゃってますが。
あえてループで書き直すならこういうことですね。
// 領域内の各列について。
for (let u = u0; u <= u1; u++) {
let empty = true;
for (let v = v0; v <= v1; v++) {
if (board[C(u,v)] !== 0) {
empty = false;
break;
}
}
// 全要素が空なら経路発見
if (empty) return true;
}
// 見つからなければ経路なし。
return false;
最後の test 関数は、
座標 p,q が同一でなくかつ絵柄が一致しているという条件の元、
XYX と YXY について pass を呼び出して経路の有無を判定しています。
上の方で定義した fromYX はここで使いました。
さて、これでゲームモデル完成。
あとは、
-
createで新規状態を生成。 - クリックされたら
updateしてゲーム状態を更新。 - それを描画。
の繰り返しです。
描画は特に何で作ってもよい部分なので略。
今回は素直に DOM いじりしてます。
詰み判定に関して
単に、同じ柄の牌の組に順次 test を走らせてるだけです。
生成時の判定も、手当たり次第に消していって詰んでいなければ開始。
詰んでいたら、ウェイト挟んで再生成、としています。
で、実際に使われている方法としては、他に
- 事前に詰まない問題を作りためたうえで、柄だけ入れ替える
- 回数限定のシャッフル機能を入れる
などがあるようです。
そもそも何で四川省の話なんかしだしたのか
ショートコーディングにハマってて短く出来そうだったからです。
というわけで 9 行四川省。詰み判定など諸々は無し。
ascii 版 (牌の代わりに英数字)
実行:github.io
<body onload="C=[t=[b=[{max:M,min:N,random:R}=Math]]];for(n=i=136;i--;w=21)t[i]
=i>>2;X=p=>p%w;Y=p=>p/w|0;for(q=k=0;k<252;c.style=`font:9mm/1 monospace;cursor:
default`){let p=k++;d=N(x=X(p),y=Y(p),w+~x,12+~y);r=x?r:T.insertRow();C[p]=c=r.
insertCell();b[p]=v=d?d-1?1+t.splice(n--*R(c.onclick=_=>{C[q||p].style.outline=
q?'none':'solid';R=(n,s,m,f,J=n=>n<m?J(n+1,s=f(s)(n)):s)=>J(n);T=(p,q,U,V,D,E,F
=p=>b[p-D]?p:F(p-D))=>!R(M(U(F(p)),U(F(q))),D=-D,N(U(F(p)),U(F(q)))+1,n=>u=>n*R
(N(s=V(p),t=V(q))+1,0,M(s,t),n=>v=>n+b[v*E-u*D]));q=q?p-q&&b[p]==b[q]&&(T(p,q,X
,Y,1,w)||T(p,q,Y,X,w,1))?(C[p][I]=C[q][I]='',b[p]=b[q]=0):0:p}),1)[0]:0:-1;c[I=
'innerHTML']=v?v>0?`&#`+(v>9?55+v:48+v):'#':''}"><table id=T>
emoji 版 (麻雀牌の絵文字がある環境のみ)
実行:github.io
<body onload="C=[t=[b=[{max:M,min:N,random:R}=Math]]];for(n=i=136;i--;w=21)t[i]
=i>>2;X=p=>p%w;Y=p=>p/w|0;for(q=k=0;k<252;c[I='innerHTML']=v?`&#`+(126975+(~v?v
:44)):''){let p=k++;d=N(x=X(p),y=Y(p),w+~x,12+~y);r=x?r:T.insertRow();C[p]=c=r.
insertCell();b[p]=v=d?d-1?1+t.splice(n--*R(c.onclick=_=>{C[q||p].style.outline=
q?'none':'solid';R=(n,s,m,f,J=n=>n<m?J(n+1,s=f(s)(n)):s)=>J(n);T=(p,q,U,V,D,E,F
=p=>b[p-D]?p:F(p-D))=>!R(M(U(F(p)),U(F(q))),D=-D,N(U(F(p)),U(F(q)))+1,n=>u=>n*R
(N(s=V(p),t=V(q))+1,0,M(s,t),n=>v=>n+b[v*E-u*D]));q=q?p-q&&b[p]==b[q]&&(T(p,q,X
,Y,1,w)||T(p,q,Y,X,w,1))?(C[p][I]=C[q][I]='',b[p]=b[q]=0):0:p}),1)[0]:0:-1;c.
style=`cursor:default;font:6mm/1.3''`}"><table id=T>
まあ、これも実装例ということでどうかひとつ...。
ショートコーディング楽しい。