記事が削除されていた(多分誤作動で消えた)ので再投稿
この記事は 慶應義塾大学SFC村井&徳田研 RG Advent Calendar 2017 の21日目の記事です。
『コマンドのベクタ表現によるSSHセッションにおける異常検知』
1. はじめに
前回、クソみたいな記事を書いてしまったことを反省し、もう少し知識をつけてからこの分野に関して書こうと思ったので投稿した。
前回の展望では「機械学習を用いて異常検知がしたい」と抜かしていたので今回はそれに関して書いていこうと思う。
今回の内容
入力コマンドごとにベクトル表現をし、SSHのコマンド入力の際に侵入者が入力したコマンド群の1セッションを1センテンスとみなすことで自然言語処理的な発想で入力コマンドのスコアリングを行い異常検知を行う。
1'. ざっくり何をやっているか
今回の話ではWord2vecのskip-gramというモデルを使用する訳であるが、このskip-gramは入力した単語に対してその前後周辺(ウィンド)になんの単語が出現しやすいかというものをモデル化したものであり、この過程において入力層から隠れ層への重みを学習させることこそが今回の目的となる。
この入力層から隠れ層への重みこそがまさに単語ベクトルであり、この単語ベクトルの表現を分散表現という。
この分散表現は以下のskip-gramの図中の入力層から隠れ層(Hidden layer)への重み、図中では
\ W_{V×N} \
によって得ることができる。
引用元: ”word2vec Parameter Learning Explained”
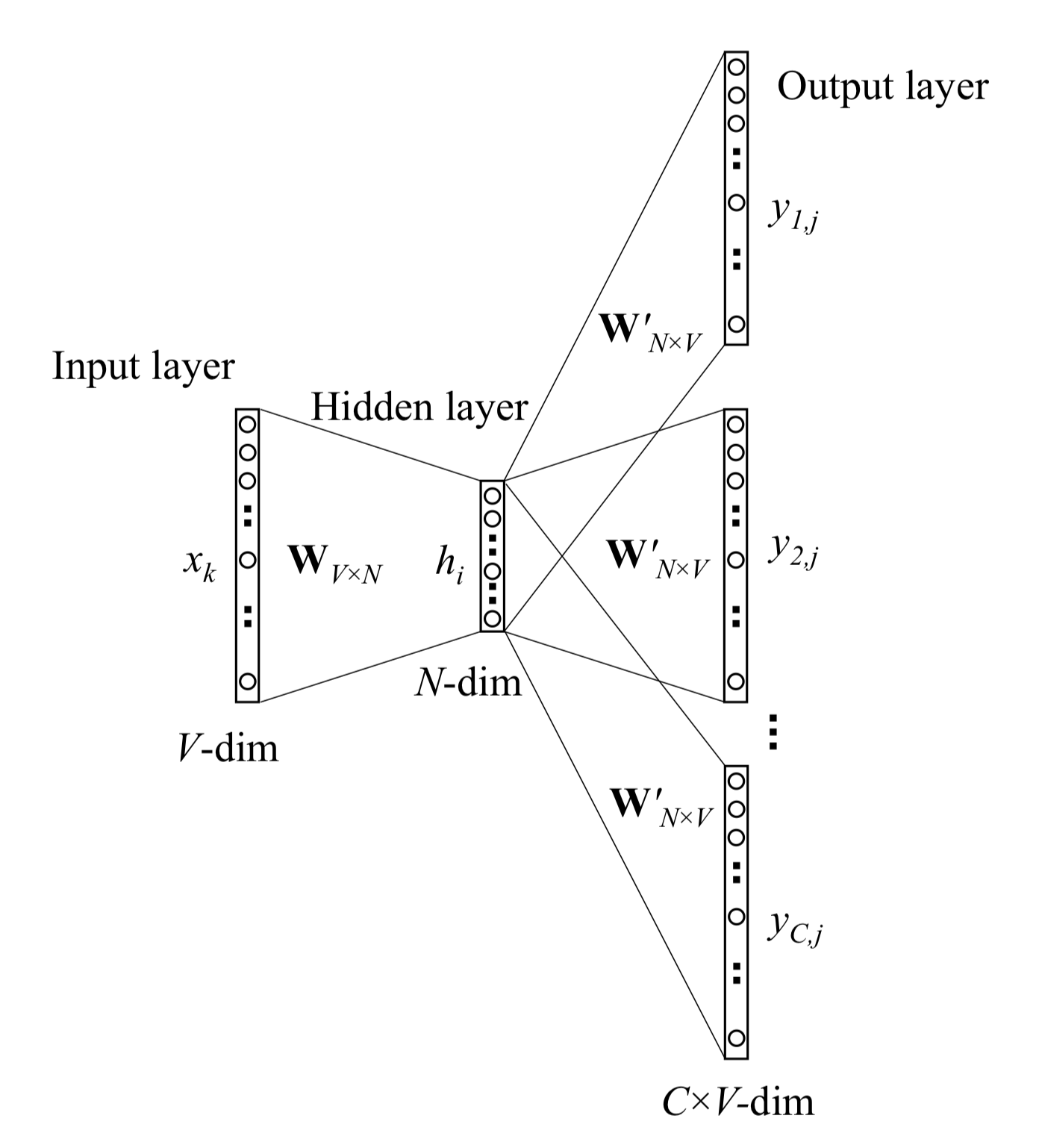
また上図のOutput layerにおける
\ y_{1j} , y_{2j} ... y_{Cj}\
はコンテキストサイズ(ウィンドサイズ)のことである。
この隠れ層の重みを抽出することこそがword2vecにおける要である。
というのも、入力層と出力層に同じデータを入れて行い、また恒等出力が出来ないくらい入力データの次元よりも遥かに小さい次元の隠れ層で学習を行わせているのである。
次の例はword2vecの単語ベクタ表現の例としてよく使われるものである。
引用元: ”word2vec Parameter Learning Explained”
king – man + woman = queen のような表し方ができる。
実際にこのword2vecを使う際の過程を見ていく。
ここでのウィンドウサイズは考慮しないこととする。
まずInput layerでは入力データをone-hotベクトルとして表す。
例えば 『 I had no progress today as well . 』 という英文があったとする。
この文のボキャブラリは
\begin{pmatrix}
as & I & had & no & progress & today & well & . \\
\end{pmatrix}
であり、ボキャブラリ数(重複のない単語の数)は8である。
このボキャブラリで**「progress」**を入力データとして入れる場合に入力されるベクトルは
\begin{bmatrix}
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
\end{bmatrix}
である。
ちなみに言うまでもないが
\begin{bmatrix}
0(as) & 0(I) & 0(had) & 0(no) & 1(progress) & 0(today) & 0(well) & 0(.) \\
\end{bmatrix}
だからである。
何かいくつかの決まったルールを決める際によくフラグメントという機能を使用するがそれと似てる。(パケットのヘッダとか)
ここで100次元の単語ベクトルを学習させることを考える。
100次元と聞くと何やそれとなるので簡単にいうと、隠れ層の100個のニューロンのことである。
また100次元の単語ベクトルのボキャブラリ数は8である。(実際にこのようなボキャブラリ数では全く足りないが、先の例で出したこともあり便宜上そうしている)
このone-hotベクトルを、学習させるデータである100(次元)×8(ボキャブラリ数)の単語ベクトルに掛けてやることでその単語のベクトルを抽出することができる。
つまり以下のような行列式ができる。
\begin{bmatrix}
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
\end{bmatrix}
\times
\begin{bmatrix}
12 & 81 & 23 & ... & (←100個 \\
41 & 32 & 8 & ... \\
7 & 63 & 61 & ... \\
96 & 2 & 85 & ... \\
29 & 99 & 17 & ... \\
19 & 61 & 88 & ... \\
45 & 49 & 69 & ... \\
39 & 31 & 7 & ... \\
\end{bmatrix}
つまり、この行列計算から導かれる行列は2項目の100×8の方の行列の5行目の
\begin{bmatrix}
29 & 99 & 17 & ... \\
\end{bmatrix}
であり、このようにone-hotベクトルはインデックス的に効率良く単語ベクトルを抽出することができる。
今の例でいうと
\begin{bmatrix}
29 & 99 & 17 & ... \\
\end{bmatrix}
が**「progress」**の単語ベクトルである。
ここまで聞いていると隠れ層はただ単に入力データを照会しているだけじゃないかと思われるかもしれないが、実際Word2vecのモデルであるskip-gramの隠れ層ではこのように活性化関数を用いていないので、実際その通りなのである。
またWord2vecに関わらず、Deep Learningでは隠れ層に活性化関数を用いる場合がある。
今回は活性化関数を用いているものではないがWord2vecの実装では活性化関数を用いるかどうかをフラグメントで指定することができる。
この入力層から隠れ層までには活性化関数を用いていないのでかなり要約して説明すると、活性化関数は入力されたデータをどのようにして活性化するかを指定する働きを持つ。
主要な活性化関数にはステップ関数、シグモイド関数、ReLU関数、ソフトマックス関数、恒等関数というものがあり、ステップ関数とシグモイド関数とソフトマックス関数に関しては入力データの総和を0.0~1.0の間に押し込める関数で、ReLU関数は入力値が0以上ならば入力値と同じ値を返し0以下なら0を返すという関数、恒等関数は入力した値をそのまま出力する関数である。
**「progress」**の単語ベクトルが導かれたところで話が逸れてしまったが、次に入力データに入力層から隠れ層の重みをかけたものを隠れ層から出力層への重みに掛ける。
ここでの単語ベクトルは先の100(次元)×8(ボキャブラリ数)の単語ベクトルを転置させて縦にしたもので、以下の通りである。
\begin{bmatrix}
12 & 41 & 7 & 96 & 29 & 19 & 45 & 39 \\
81 & 32 & 63 & 2 & 99 & 61 & 49 & 31 \\
23 & 8 & 61 & 85 & 17 & 88 & 69 & 7 \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
(↑100個 & . & . & . & . & . & . & . \\
\end{bmatrix}
これに先ほど求めた**「progress」**の単語ベクトルを掛ける。
ここで大事なことは
\begin{bmatrix}
12 & 41 & 7 & 96 & 29 & 19 & 45 & 39 \\
81 & 32 & 63 & 2 & 99 & 61 & 49 & 31 \\
23 & 8 & 61 & 85 & 17 & 88 & 69 & 7 \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
(↑100個 & . & . & . & . & . & . & . \\
\end{bmatrix}
の行列を**「progress」**の単語ベクトルを掛ける時を考えて欲しいのだが、
1列目に注目してほしい。
\begin{bmatrix}
12 \\
81 \\
23 \\
. \\
. \\
. \\
. \\
. \\
\end{bmatrix}
これは、入力層から隠れ層までの重みベクトルの1行目
\begin{bmatrix}
12 & 81 & 23 & ... & (←これ \\
41 & 32 & 8 & ... \\
7 & 63 & 61 & ... \\
96 & 2 & 85 & ... \\
29 & 99 & 17 & ... \\
19 & 61 & 88 & ... \\
45 & 49 & 69 & ... \\
39 & 31 & 7 & ... \\
\end{bmatrix}
と同じであり、つまりone-hotベクトルにおいて
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
とした時に抽出されるものと同じ、さらに言えば下図より**「as」の単語ベクトル**と言え、
\begin{bmatrix}
1(as) & 0(I) & 0(had) & 0(no) & 0(progress) & 0(today) & 0(well) & 0(.) \\
\end{bmatrix}
**「progress」**の単語ベクトルと、隠れ層から出力層への重みベクトルをかけた以下の行列式は
\begin{bmatrix}
29 & 99 & 17 & ... \\
\end{bmatrix}
\times
\begin{bmatrix}
12 & 41 & 7 & 96 & 29 & 19 & 45 & 39 \\
81 & 32 & 63 & 2 & 99 & 61 & 49 & 31 \\
23 & 8 & 61 & 85 & 17 & 88 & 69 & 7 \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
. & . & . & . & . & . & . & . \\
(↑100個 & . & . & . & . & . & . & . \\
\end{bmatrix}
↓
\begin{bmatrix}
29 & 99 & 17 & ... \\
\end{bmatrix}
\times
\begin{bmatrix}
as & I & had & no & progress & today & well & . \\
の & の & の & . & . & . & . & . \\
単 & 単 & . & . & . & . & . & . \\
語 & 語 & . & . & . & . & . & . \\
ベ & ベ & . & . & . & . & . & . \\
ク & ク & . & . & . & . & . & . \\
ト & ト & . & . & . & . & . & . \\
ル & ル & . & . & . & . & . & . \\
\end{bmatrix}
で表すことができ、これから導き出されるものは
\begin{bmatrix}
入~隠の単語ベクトル\\
\end{bmatrix}
\times
\begin{bmatrix}
隠\\
~\\
出\\
の\\
単\\
語\\
ベ\\
ク\\
ト\\
ル\\
\end{bmatrix}
なのであり、これにソフトマックス関数をかませることで各単語の予測確率を出力することが可能である。
疲れたため、 物事のニュアンス的な理解を深めるため、パラメータやNegative Samplingなどに関する説明はここでは割愛しよう。
おわかりいただけだろうか。
2. 環境
- OS
- Ubuntu --version 16.04 LTS
- システム
- Honeypot kippo
- 言語,ライブラリ等
- Python --version 3.5.2
- TensorFlow --version 1.4.0
- gensim --version 0.12.4
-- 構成 --
command_predict
├── shaping.py
├── train.py
├── similarword.py
├── command.txt
├── command.model
└── result.txt
3.ソースコード本文と手順
今回は宗教上の理由でPythonでの実装を行いたいので、GensimというライブラリのWord2Vecの実装を用いた。
まずはHoneypotのログを取得、整形していこう。
攻撃ログは自身のHoneypotでの攻撃ログを用いてもいいのではあるが(Honeypotを動かし始めてから1年以上たつのである程度は貯まっている)、データ量の観点からこちら("セキュリティ・キャンプ アワード2016"より)の攻撃ログを学習データとして用いた。
このファイル形式はtsvであるが、csvもtsvも変わらんので特に必要なことはない。
整形はこちらを大変参考にした。
# -*- coding:utf-8 -*-
import csv
with open('session_command.tsv', 'r') as f:
doc = [row for row in csv.reader(f, delimiter='\t')]
for row in doc:
row.pop(0)
with open('command.txt', 'w') as f:
w = csv.writer(f, delimiter='\t', lineterminator='\n')
w.writerows(doc)
次にgensimを使っていこう。
まずはinstallから。
apt-get install gfortan libblas-dev liblapack-dev python3-dev python3-pip
pip3 install numy scipy
pip3 install gensim
後々高速化のために使うのでこちらも入れておこう。
pip3 install cython
apt-get install ipython3
さてこれで下準備はできたので次はword2vecを用いた学習を行っていく。
パラメータの設定は個人でやっていただければいいと思う。
こちらの記事がオプションの設定に際して大変参考になった。
# -*- coding: utf-8 -*-
from gensim.models import word2vec
import logging
import sys
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.IN FO)
sentences = word2vec.LineSentence(sys.argv[1])
model = word2vec.Word2Vec(sentences,
sg=1, #skip-gramモデルの使用の有無,sg=0ならcbowモデルになる.
size=300, #単語ベクトルの次元数.先の説明で言うと隠れ層のニューロンの数である.
min_count=1, #何回未満の登場まで登場する単語を破棄するか
window=10, #ウィンドウサイズ(コンテキストサイズ).先の説明の周辺語の数である.
hs=1, #階層化ソフトマックス関数の使用の有無
negative=0) #ネガティブサンプリングに用いる単語の数
model.save(sys.argv[2])
次にモデルの作成を行う。
python train.py command.txt command.model #train.pyとcommand.txtは同dir
これで先に定めたパラメータでの入力コマンドのcommand.modelというモデルが生成できた。
次は生成モデルを用いてコマンドの類似予測を行なっていこう。
# -*- coding: utf-8 -*-
from gensim.models import word2vec
import sys
import numpy as np
model = word2vec.Word2Vec.load(sys.argv[1])
results = model.most_similar(positive=sys.argv[2], topn=10)
print('-----------------------------------------')
print('The command of your choice')
print('"', sys.argv[2] , '"')
print('Next predicted command is ...')
for result in results:
print(result[0], '\t', result[1])
print('-----------------------------------------')
では実際にコマンド類似予測を行なってみよう。
今回はコマンド"cd"の予測を行なってみる。
python similarword.py command.model cd
-----------------------------------------
The command of your choice
" cd "
Next predicted command is ...
/var/run 0.9216534495353699
/var 0.9082216024398804
/mnt 0.8984242677688599
/tmp 0.888166606426239
/dev/shm 0.8751758337020874
/ 0.846301257610321
/var/tmp 0.8359629511833191
/root 0.7447156310081482
/bin/ 0.7377800941467285
home 0.7329117655754089
-----------------------------------------
かなりいい結果になったのではないかと思われる。
あとはたくさんの単語での結果が欲しいのでBusyBoxの全コマンドを先ほどのsimilarword.pyにfor文を使ってかけてみた。
結果はこちらにあげたので気になる方はどうぞ。
4. 終わりに
前篇はここまでである。
後編があるかはわからないがに期待して欲しい。
機械学習というものを触ってから数えるほどの日しか経っておらず導入部分から説明臭い記事になってしまったので無論高度なものではなくなってしまったが、基礎から色々知ることできて勉強になったのでまぁよしとする。
5. わからなかったこと
コンテキストサイズに関して以下の図の

\ y_{1j} , y_{2j} ... y_{Cj}\
がなぜユニットがコンテキストサイズの出力がそれぞれの値を持つのかがいまいちしっくりこなかった。
\ w_{I}\
は唯一の入力のはずであるが、ユニットの数が複数ある場合に各々の出力がどのようになるのか具体的に知りたい。
参考文献
絵で理解するWord2vecの仕組み
Word2Vec のニューラルネットワーク学習過程を理解する
数式からみるWord2Vec
深層学習:ハイパーパラメータの設定に迷っている人へ
gensim/word2vec.py