前回の続き
前回は $Poisson$ 方程式を解いた.今回は時間発展する拡散方程式を解く.
コードはこちらから.
拡散方程式
\nabla^2 \boldsymbol{f} = C \frac{\partial \boldsymbol{f}}{\partial t}
時間と空間による微分
時間微分は若干トリッキー.
\frac{\partial \boldsymbol{f}}{\partial t}\Biggl|_{t=t+\Delta t} = \frac{1}{C}\nabla^2 \boldsymbol{f}(t+\Delta t) \\
\frac{\partial \boldsymbol{f}}{\partial t}\Biggl|_{t=t} = \frac{1}{C}\nabla^2 \boldsymbol{f}(t)
上のような2つの偏微分を考え,これらの内分を取る.つまり,
\frac{\partial \boldsymbol{f}}{\partial t}\simeq
\frac{\boldsymbol{f}(t + \Delta t) - \boldsymbol{f}(t)}{\Delta t} \simeq
\alpha\frac{1}{C}\nabla^2 \boldsymbol{f}(t+\Delta t) + (1 - \alpha)\frac{1}{C}\nabla^2 \boldsymbol{f}(t)
というような近似を考える.実際には $\alpha = 1$ のときの精度が高くなる(らしい).したがって,
\frac{\boldsymbol{f}(t + \Delta t) - \boldsymbol{f}(t)}{\Delta t}\simeq
\frac{1}{C}\nabla^2 \boldsymbol{f}(t+\Delta t) \\
\boldsymbol{f}(t + \Delta t) - \frac{\Delta t}{C}\nabla^2 \boldsymbol{f}(t+\Delta t) = \boldsymbol{f}(t)
前回の投稿から,$Poisson$ 方程式の立式は
\nabla^2 \boldsymbol{f} = \phi(x) \\
L\boldsymbol{f} = \boldsymbol{\psi}
となった.$\phi(x)=0$ であるときの $\boldsymbol{\psi}$ (常に一定)を代入すると,
\boldsymbol{f}(t + \Delta t) - \frac{\Delta t}{C}\bigl(L \boldsymbol{f}(t+\Delta t)- \boldsymbol{\psi}\bigl) = \boldsymbol{f}(t) \\
\Bigl(I - \frac{\Delta t}{C}L\Bigl)\boldsymbol{f}(t+\Delta t) = \boldsymbol{f}(t)-\frac{\Delta t}{C}\boldsymbol{\psi}
を得ることができる.
これによって,$I - \frac{\Delta t}{C}L$ の逆行列を求めることによって,時間発展する $\boldsymbol{f}$ を求めることができる.
実問題を解く
例えば,ある金属板の時間発展する温度の拡散を求める場合は考慮すべき拡散方程式は以下の通り.
\lambda \nabla^2 T = C_p \frac{\partial T}{\partial t}
ここで $\lambda$ は熱伝導率で $C_p$ は熱容量.上で解いた式の$C$ に $C = \frac{C_p}{\lambda}$ を代入することで,
\Bigl(I - \frac{\lambda\Delta t}{C_p}L\Bigl)\boldsymbol{f}(t+\Delta t) = \boldsymbol{f}(t)-\frac{\lambda\Delta t}{C_p}\boldsymbol{\psi} \\
\boldsymbol{f}(t+\Delta t) = \Bigl(I - \frac{\lambda\Delta t}{C_p}L\Bigl)^{-1}\Bigl(\boldsymbol{f}(t)-\frac{\lambda\Delta t}{C_p}\boldsymbol{\psi}\Bigl)・・・(A)
を得る.両辺の内,$\boldsymbol{f}(t+\Delta t)$ を除いて全ての項が既知であり,一定である.
そのため,以下のような手順で解けばよい.
1.$\Bigl(I - \frac{\lambda\Delta t}{C_p}L\Bigl)$ と $\frac{\lambda\Delta t}{C_p}\boldsymbol{\psi}$ を計算する.
2.$\Bigl(I - \frac{\lambda\Delta t}{C_p}L\Bigl)$ の逆行列を求める.
3.初期条件 $\boldsymbol{f}(0)$ を設定する.
4.(A) に前のステップで得た $\boldsymbol{f}(t)$ を代入することで次のステップの計算に使う $\boldsymbol{f}(t+\Delta t)$ を求める.
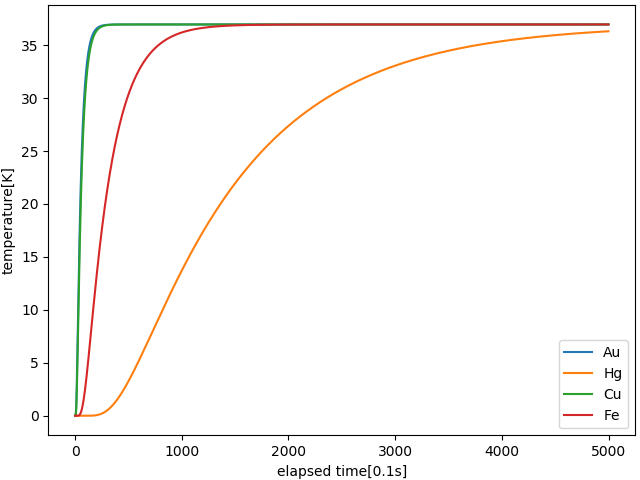
以上のようなことを繰り返すことで $\boldsymbol{f}$ の時系列データを得る.今回は金,水銀,鉄,銅の4種類の10cm四方の金属に対してある点の温度の時間推移を計算した.
結果は以下の通り.
金の温度拡散 pic.twitter.com/Xre6AwGkH6
— shuhei watanabe (@shuheiwatanabe3) March 6, 2019
銅の温度拡散 pic.twitter.com/3ct5jbr388
— shuhei watanabe (@shuheiwatanabe3) March 6, 2019
鉄の温度拡散 pic.twitter.com/hhOrfQtx9u
— shuhei watanabe (@shuheiwatanabe3) March 6, 2019
水銀の温度拡散 pic.twitter.com/pUo7uxzvQ2
— shuhei watanabe (@shuheiwatanabe3) March 6, 2019
熱伝導率の高い金属はものの数秒の間に温度拡散が終了してしまった一方で熱伝導率の低い水銀は熱が伝わるまでに時間がかかっている.時間の違いはあれど,最終的に材料によらず収束する温度が同じになる結果は面白い.