はじめに
物理学のシミュレーションにおいては微分方程式を解くことが重要である.物理現象は大きく分けると以下の形式に分類可能.
コードはこちらから.
$Poisson$ 方程式 (今回扱う)
\nabla^2 f = \phi (x)
$Laplace$ 方程式
\nabla^2 f = 0
拡散方程式
\nabla^2 f = C \frac{\partial f}{\partial t}
波動方程式
\nabla^2 f = C \frac{\partial^2 f}{\partial t^2}
差分法
微分方程式を扱う際には微分を行う必要がある.しかし,実際に微分を行うことができない場合が通常である.したがって微分の近似を考える際に差分法を用いる.差分法にはルンゲクッタ法のような精度の高い手法も存在するが,ここでは単純な手法のみ紹介.
$f(x)$ が定義域内で連続でかつ $n$ 回微分可能な関数であれば,以下のような $Taylor$ 展開を以下のように定義することができる.
f(x+\Delta x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(x)}{n!}\Delta x^n ・・・(A)\\
f(x-\Delta x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(x)}{n!}(-1)^n \Delta x^n ・・・(B)
(A)を変形すると,前進差分.
f(x+\Delta x) - f(x) = \Delta xf'(x) + o(\Delta x^2) \\
f'(x) = \frac{f(x+\Delta x) - f(x)}{\Delta x} + o(\Delta x) ・・・(A)'\\
(B)を変形すると,後退差分.
f(x-\Delta x) - f(x) = -\Delta xf'(x) + o(\Delta x) \\
f'(x) = \frac{f(x) - f(x-\Delta x)}{\Delta x} + o(\Delta x) ・・・(B)'\\
(A)ー(B)を変形すると,中心差分.
f(x+\Delta x) - f(x-\Delta x) = 2\Delta x f'(x) + o(\Delta x^3) \\
f'(x) = \frac{f(x + \Delta x) - f(x - \Delta x)}{2\Delta x} + o(\Delta x^2)・・・(C)
(A)+(B)を変形すると,2階微分の中心差分
f(x+\Delta x) + f(x-\Delta x) = 2f(x) + \Delta x^2f''(x)+o(\Delta x^3) \\
f''(x) = \frac{f(x+\Delta x) - 2f(x) + f(x-\Delta x)}{\Delta x^2} + o(\Delta x)・・・(D)
今回は$\Delta x$ が十分に小さく $o(...)$ の部分は無視できる程度であるという仮定のもとに上の微分の近似式を用いる.
プログラムに落とし込む
今回は簡単のために2次元 $Laplace$ 方程式のプログラムを行う.つまり,以下のような式を扱う.
\nabla^2 f = \phi (x) \\
\frac{\partial ^2f}{\partial x^2} + \frac{\partial ^2f}{\partial y^2} = \phi (x, y)
空間の分割
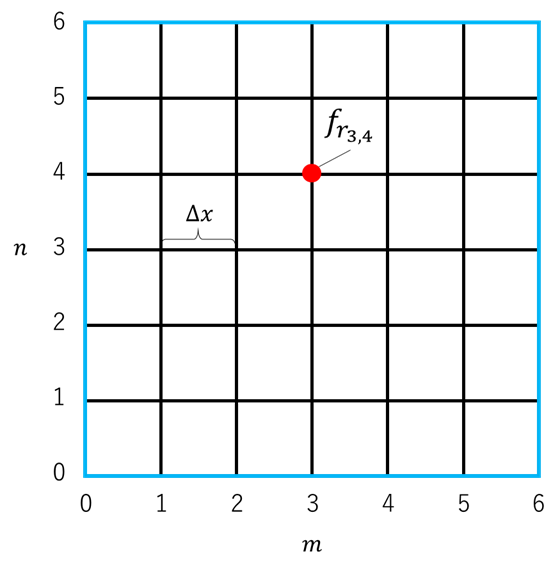
最初に差分法を用いるために空間をグリッド状に区切る必要がある.したがって,$0 \leq x \leq (m+1)\Delta x,\ 0 \leq y \leq (n+1)\Delta y$ ($m,\ n$は自然数)に区切る.$f(x,y)$ は任意の非負整数 $0 \leq i \leq m + 1, 0 \leq j \leq n + 1$ による $(i\Delta x,\ j\Delta y)$ 上でのみ定義される.シミュレーションを解くためには境界条件が必要になるため,$i=0,m+1$ または $j=0,n+1$ のグリッド上の点の値 $f$ は既知であるものとする.
また,$i,j$ によって,グリッド上の点を一意に求めることができるので,$r_{i,j} = (i-1) + m(j-1)$ とする.また,簡単のため, $f(i\Delta x,\ j\Delta y)=f_{r_{i,j}}$ とする.
上の画像の水色部分が境界条件,グリッド上の点が未知点である.
式の近似
(D)の近似式を用いると,
\frac{\partial ^2f_{r_{i,j}}}{\partial x^2} \simeq \frac{f_{r_{i+1,j}} - 2f_{r_{i,j}} + f_{r_{i-1,j}}}{\Delta x^2} \\
\frac{\partial ^2f_{r_{i,j}}}{\partial y^2} \simeq \frac{f_{r_{i,j+1}} - 2f_{r_{i,j}} + f_{r_{i,j-1}}}{\Delta y^2}
この2式を足し合わせると,
\phi _{r_{i,j}} = \frac{\partial ^2f_{r_{i,j}}}{\partial x^2} + \frac{\partial ^2f_{r_{i,j}}}{\partial y^2}
\simeq \frac{f_{r_{i+1,j}} - 2f_{r_{i,j}} + f_{r_{i-1,j}}}{\Delta x^2} + \frac{f_{r_{i,j+1}} - 2f_{r_{i,j}} + f_{r_{i,j-1}}}{\Delta y^2} \\
= \frac{1}{\Delta x^2}f_{r_{i+1,j}} + \frac{1}{\Delta x^2}f_{r_{i-1,j}} + \Biggl(\frac{-2}{\Delta x^2}+\frac{-2}{\Delta y^2}\Biggl)f_{r_{i,j}} + \frac{1}{\Delta y^2}f_{r_{i,j-1}} + \frac{1}{\Delta y^2}f_{r_{i,j+1}}
を得ることができる.これを $r_{i,j}=0,1,2,...,mn-1 $ 全てに対して求めれば良い.また,以下では $c_1=\frac{1}{\Delta x^2},c_2=\frac{1}{\Delta y^2},c_3=\Bigl(\frac{-2}{\Delta x^2}+\frac{-2}{\Delta y^2}\Bigl)$ とする.
連立方程式の構築
上でのモデルの立式をもとに以下の方程式を解き,$\boldsymbol{f}=(f_0,f_1,...,f_{mn-1})$ を決定したい.
\begin{eqnarray}
\left\{ \begin{array}{l}
c_1 f_{r_{2,1}} + c_1 f_{r_{0,1}} +c_3 f_{r_{1,1}} + c_2 f_{r_{1,0}} + c_2 f_{r_{1,2}} = \phi _{r_{1,1}} \\
c_1 f_{r_{3,1}} + c_1 f_{r_{1,1}} +c_3 f_{r_{2,1}} + c_2 f_{r_{2,0}} + c_2 f_{r_{2,2}} = \phi _{r_{2,1}} \\
. \\
. \\
. \\
c_1 f_{r_{m,n}} + c_1 f_{r_{m-2,n}} +c_3 f_{r_{m - 1,n}} + c_2 f_{r_{m-1,n-1}} + c_2 f_{r_{m-1,n+1}} = \phi _{r_{m - 1,n}} \\
c_1 f_{r_{m+1,n}} + c_1 f_{r_{m-1,n}} +c_3 f_{r_{m,n}} + c_2 f_{r_{m,n-1}} + c_2 f_{r_{m,n+1}} = \phi _{r_{m,n}}
\end{array} \right.
\end{eqnarray}
ただし,$i=0,m+1$ または $j=0,n+1$ の点における $f$ は境界条件より既知であるから,右辺の既知辺に移項する.
すると,
\begin{eqnarray}
\left\{ \begin{array}{l}
c_1 f_{r_{2,1}} +c_3 f_{r_{1,1}} + c_2 f_{r_{1,2}} = \phi _{r_{1,1}} - c_1 f_{r_{0,1}} - c_2 f_{r_{1,0}} \\
c_1 f_{r_{3,1}} + c_1 f_{r_{1,1}} +c_3 f_{r_{2,1}} + c_2 f_{r_{2,2}} = \phi _{r_{2,1}} - c_2 f_{r_{2,0}}\\
. \\
. \\
. \\
c_1 f_{r_{m,n}} + c_1 f_{r_{m-2,n}} +c_3 f_{r_{m - 1,n}} + c_2 f_{r_{m-1,n-1}} = \phi _{r_{m - 1,n}} - c_2 f_{r_{m-1,n+1}}\\
c_1 f_{r_{m-1,n}} +c_3 f_{r_{m,n}} + c_2 f_{r_{m,n-1}} = \phi _{r_{m,n}} - c_1 f_{r_{m+1,n}} - c_2 f_{r_{m,n+1}}
\end{array} \right.
\end{eqnarray}
のように変形可能.これらを行列の形式にまとめることで,
L\boldsymbol{f} = \boldsymbol{\psi}
と書ける.また,これらの行列及びベクトルの要素は
\begin{eqnarray}
L_{r_{i,j},r_{i',j'}}=\left\{ \begin{array}{ll}
c_1 & (|r_{i,j} - r_{i',j'}| = 1)\\
c_2 & (|r_{i,j} - r_{i',j'}| = m)\\
c_3 & (|r_{i,j} - r_{i',j'}| = 0)\\
0 & (otherwise)\\
\end{array} \right.
\end{eqnarray}
\begin{eqnarray}
\boldsymbol{\psi_{r_{i,j}}}= \phi_{r_{i,j}} - \left\{ \begin{array}{ll}
c_1 f_{r_{0,j}} & (i = 0)\\
c_1 f_{r_{m,j}} & (i = m)\\
c_2 f_{r_{i,0}} & (j = 0)\\
c_2 f_{r_{i,n}} & (j = n)\\
0 & (otherwise)\\
\end{array} \right.
\end{eqnarray}
となる.$\psi$ の右辺は条件に応じて必要な値を引くことで要素の値を得ることが可能.これで $Poisson$ 方程式の立式を終えた.あとは $L$ の逆行列を求めることによって $\boldsymbol{f}$ を得る.
実問題を解く
上までのモデル化によって,グリッドサイズ $\Delta x, \Delta y$, グリッド数 $m, n$,境界条件 $f_{r_{0,j}},f_{r_{m+1,j}},f_{r_{i,0}},f_{r_{i,n+1}}$ さえ与えれば,定義された空間における $\boldsymbol{f}$ を得ることができる.
今回はここにある中の熱伝導による温度分布の項目のモデル化に取り組む.
熱源の分布を $s(x)$,熱伝導率を $\lambda$,温度分布を $T$ としたときの関係性.
\nabla^2T = - \frac{s}{\lambda} = 0
を用いる.今回は特定の熱源が存在しない,つまり,$s(x)=0$ の場合の熱拡散をシミュレーションする.
LT = \boldsymbol{\psi}
の $L^{-1}$ を求めて両辺に左からかけることによって,定常状態の温度分布 $T$ が判明する.
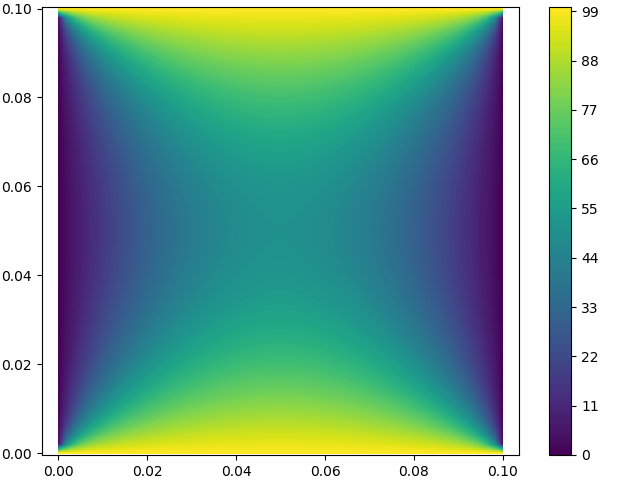
上の境界条件でかつ熱源がない状態で定常状態の温度分布を求めてみる.
実際に求めてみるとこんな感じになった.対称的になっていて直感に当てはまるような結果を得た.