学習率の調整、予め足すか？後から足すか？ #機械学習

AdaGradは言わずと知れた、特徴ごとに学習率を自動的に調整するアルゴリズムである。Hivemallの実装で初期パラメータを再考する機会があったのだけど、初期パラメータのあり方に疑問を持つ部分があって整理したかったのでこのエントリを書いている

AdaGrad recap

AdaGradではg：勾配、w：特徴の重みの配列に対して次のように更新する。

gg[i] += g * g;
η = eta / (sqrt(gg[i]) + eps);
w[i] -= η * g;

ここで、gg：初期値0.0の配列、eta：学習率の定数、ηが学習率。
AdaGradでは、勾配の二乗を訓練事例ごとに加えて、学習率をggで割ることで学習率の自動調整を行う。基本的には訓練が進むごとにαを小さくしていかないと学習が収束しない。

ChainerでもTensorFlowでもKerasでも同様に実装されている。

epsの初期値はゼロ除算を避ける為だったりで0に近い小さな値を使うことが良いとされる。
Chainerの実装だとデフォルトでeps=1e-8, etaが0.001となっている。

この記事でもあるように、epsが0に近い値だとすると最初の重みの更新がetaとほぼ等しくなり、比較的分かりやすい挙動となる。

eta / sqrt(g * g) * g = eta

ただし、最初の重みの更新が w[i] -= eta というのは理想的だろうか(?)

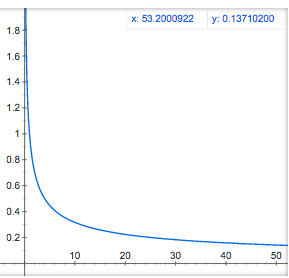
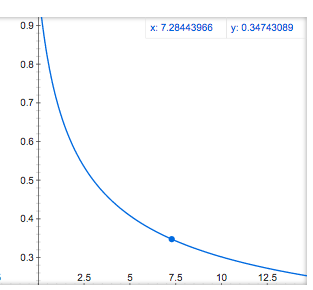
epsが0に近い場合は、1/sqrt(x)の補正が行われる。次のような感じのスロープとなる。

ggが0.01だったりするとeta * 10であったりするのでかなりaggressiveに更新が行われる。

Hivemallだとetaの初期値から基本的に学習率が下がっていくようにしたいという考えから、この記事と同様、epsの初期値は1.0として η = eta / (sqrt(eps + gg[i])) を利用している。こうすると基本的に学習率がeta以下となる。

以下のように、学習率の調整に勾配gは利用しないものとする。η * gで更新するのに学習率の調整をその時の勾配gで調整するというのがどこか引っかかる（過去の勾配なら良いけど）。

gg = gg[i];
gg[i] = gg + g * g;
η = eta / sqrt(eps + gg);
w[i] -= η * g;

この時、epsを1とすると、最初の更新時、ggは0であるので、学習率はパラメタで与えた初期学習率と等しくなる。つまり、SGDと同様の更新式となる。学習率は初期学習率etaから単調減少する。

η = eta / sqrt (1+0) = eta
w[i] -= eta * g;

論文通りにggを先に足した方が良いでしょうか？

p.s. この映画好きです。