数式(画像)をpython化するワークフロー

モチベーション

論文や教科書で数式を見つけても、それを活用するまでに時間が掛かる。ましてや、ドキュメントに落とすとなると更に時間が掛かってしまう。
そこで、数式画像をインプットとして、プログラミングに利用でき、かつ、その後のドキュメント化にも利用できるワークフローを作った。
※全自動は難しいので、人との協働作業です。

画像からlatex化

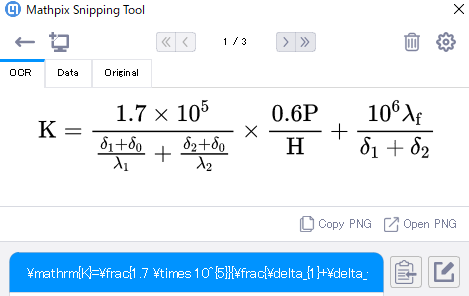
Mathpixというサービスを使用してlatex化します。登録などは必要ですが、いい感じで画像をlatex化してくれます。

こんな感じです

AsciiMathの文字列を取得する

AsciiMathの文字列を加工して、pythonで利用できる形に変換していきます

• Mathpixの"data"タブのAsciiMathをコピーする
  この文字列を元に、プログラムで利用できるようにしていきます。

前処理

文字列に前処理を施します

• a : AsciiMathの文字列をペースト
• shoki_dict : 一番最初に置換していく辞書　※随時更新

translate_1.py

import re
# a = "sigma=(E alpha DeltaT)/(1-nu)*(1)/(1.5+3.25//beta-0.5 exp(-16//beta))"
# a = "M_(max)=(w*l^(2))/(8)"
a= "delta_(max)=(5*w*l^(4))/(384 E*I)"
# a ="K=(1.7 xx10^(5))/((delta_(1)+delta_(0))/(lambda_(1))+(delta_(2)+delta_(0))/(lambda_(2)))xx(0.6P)/(H)+(10^(6)lambda_(f))/(delta_(1)+delta_(2))"
shoki_tikan_dict = {" ":"*",
                   "xx":"*",
                   "^":"**",
                   "//":"/"}
for i in shoki_tikan_dict:
    a = a.replace(i,shoki_tikan_dict[i])
    
temp = re.sub("_\((.*?)\)","0",a)#添字を無視して変数を取得できるよう、_()を0に変換
hensu = re.findall("[A-Za-z]+",temp)#変数を抜き出します
li_moji = list(set(hensu))#変数の重複を消す
print(a)
print(li_moji)

上記を実施すると、以下が出力されます。ここで式に変な所があれば、修正します。また、変数がきちんと抽出されているかを確認します。（余分に出ているのは、無視してOK　例では、"exp"は無視)
sigma=(EalphaDeltaT)/(1-nu)(1)/(1.5+3.25/beta-0.5exp(-16/beta))
['nu', 'sigma', 'DeltaT', 'beta', 'alpha', 'exp', 'E']

式を変換

ギリシャ文字や添字を変換して式の形にしていきます

• moji_dict : パラメータ抽出時に使用するリスト（ギリシャ文字）　※随時更新

translate_2.py

moji_dict = {'lambda':"λ",
             'delta':"δ",
            'sigma':"σ",
            'alpha':"α",
            'DeltaT':"ΔT",
            'nu':'ν',
            'beta':'β',
            'epsi':"ε",
            'pi':'π',
            'mu':'μ'}


def tikan(moji_retsu,taisho,moji_dict):
#     print(taisho)
    taisho_temp = taisho+"_"
    seiki_1 = taisho_temp + "\(.*?\)"
    seiki_2 = taisho_temp + "\((.*?)\)"
    b = re.findall(seiki_1,moji_retsu)

    if len(b) != 0:
        if taisho in moji_dict:
            tikan_moji = moji_dict[taisho]
        else:
            tikan_moji = taisho
#             print(tikan_moji)
            
        newList = [re.sub(seiki_2,tikan_moji+"\\1",item) for item in b]
        moji_retsu = re.sub(seiki_2,tikan_moji+"\\1",moji_retsu)

    elif taisho in moji_dict:
        tikan_moji = moji_dict[taisho]
        newList = [tikan_moji]
        moji_retsu = moji_retsu.replace(taisho,tikan_moji)

    else:
        tikan_moji = taisho
        newList = [taisho]
        
    return moji_retsu,newList

li=[]
for i in li_moji:
    a,p = tikan(a,i,moji_dict)
    li.extend(p)
li=list(set(li))
li.sort()

a = re.sub("\(([0-9])\)","\\1",a)
print(a)
print(li)

上記を実行すると、下記が出力されます
σ=(EαΔT)/(1-ν)1/(1.5+3.25/β-0.5exp(-16/β))
['E', 'exp', 'ΔT', 'α', 'β', 'ν', 'σ']

次に、添字をつけつつ、式の形にしていきます。
自動で出来るのはここまでで、後は手動でpythonで使える式にします。

result_Eq.py

import math
σ=(E*α*ΔT)/(1-ν)*1/(1.5+3.25/β-0.5*math.exp(-16/β))

式は完成したので、次はパラメータを抽出します。

paramater_print.py

print("paramater_dict= {")
for i in li:
    print("    " + "'" + i +"':['',''],")
print("    }")

上記を実行すると、下記が出力されます。

out.py

paramater_dict= {
    'E':['',''],
    'exp':['',''],
    'ΔT':['',''],
    'α':['',''],
    'β':['',''],
    'ν':['',''],
    'σ':['',''],
    }

自動はここまでで、パラメータに対して、下記処置を手動でやります

• 不要なパラメータの削除
• 順番を変える
• 説明と単位を追加

result.py

paramater_dict= {
    'E':['ヤング率','MPa'],
    'ΔT':['内外温度差','K'],
    'α':['線膨張係数','/K'],
    'β':['ビオ数',''],
    'ν':['ポアソン比',''],
    'σ':['熱応力','MPa'],
    }

折角なので、使えるか実行

run.py

import math

E = 200
ΔT = 10
α = 0.00005
β = 2
ν = 0.3

σ=(E*α*ΔT)/(1-ν)*1/(1.5+3.25/β-0.5*math.exp(-16/β))
print(σ)

上記を実行すると、ちゃんと答えが出てきます。
0.045716739515498046

ドキュメント化

ここまでしておくと、下記記事の応用で、sympyを使って、簡単にドキュメント化できます。
python+sympyで機械系設計計算書ネタを作成する

作成した式に関して

適宜式を作成し、下記で共有していきます（適宜更新）
数式と関数(適宜更新）

あとがき

latex2sympyなどのライブラリを使おうかとも思ったのですが、なかなか難しかったです。
不得手な正規表現の勉強になりました！
会社のセキュリティの関係で、Mathpixが使えない。。。切ないなぁ