モチベーション
- 画像のコントラストをいじるトーンカーブをワンパラメータで実装したかった
- 画像のコントラスト調整のためのヒストグラムに適切な関数を探しています。ではシグモイドが推されまくっているが、シグモイドは値域が$[0,1]$ではない
- $0 \rightarrow 0$, $1 \rightarrow 1$であってほしい
PseudoSigmoidの歴史
- 『シグモイド曲線の定義域が有界でないので、有界なシグモイド曲線を勝手に作ってみた』を見つけた
- 『シグモイド関数でコントラスト強調』も見つけた
- 『ガンマ曲線とシグモイド曲線による画像補正』でも似たようなことをしている
1. シグモイドをベースにちょっと縦に伸ばす
上記『シグモイド関数でコントラスト強調』や『ガンマ曲線とシグモイド曲線による画像補正』での実装
s(x) = \frac{1}{1+e^{a(b-x)}}\\
f(x) = \frac{s(x)-s(0)}{s(1)-s(0)}
結果
https://www.geogebra.org/m/ydqszvqw
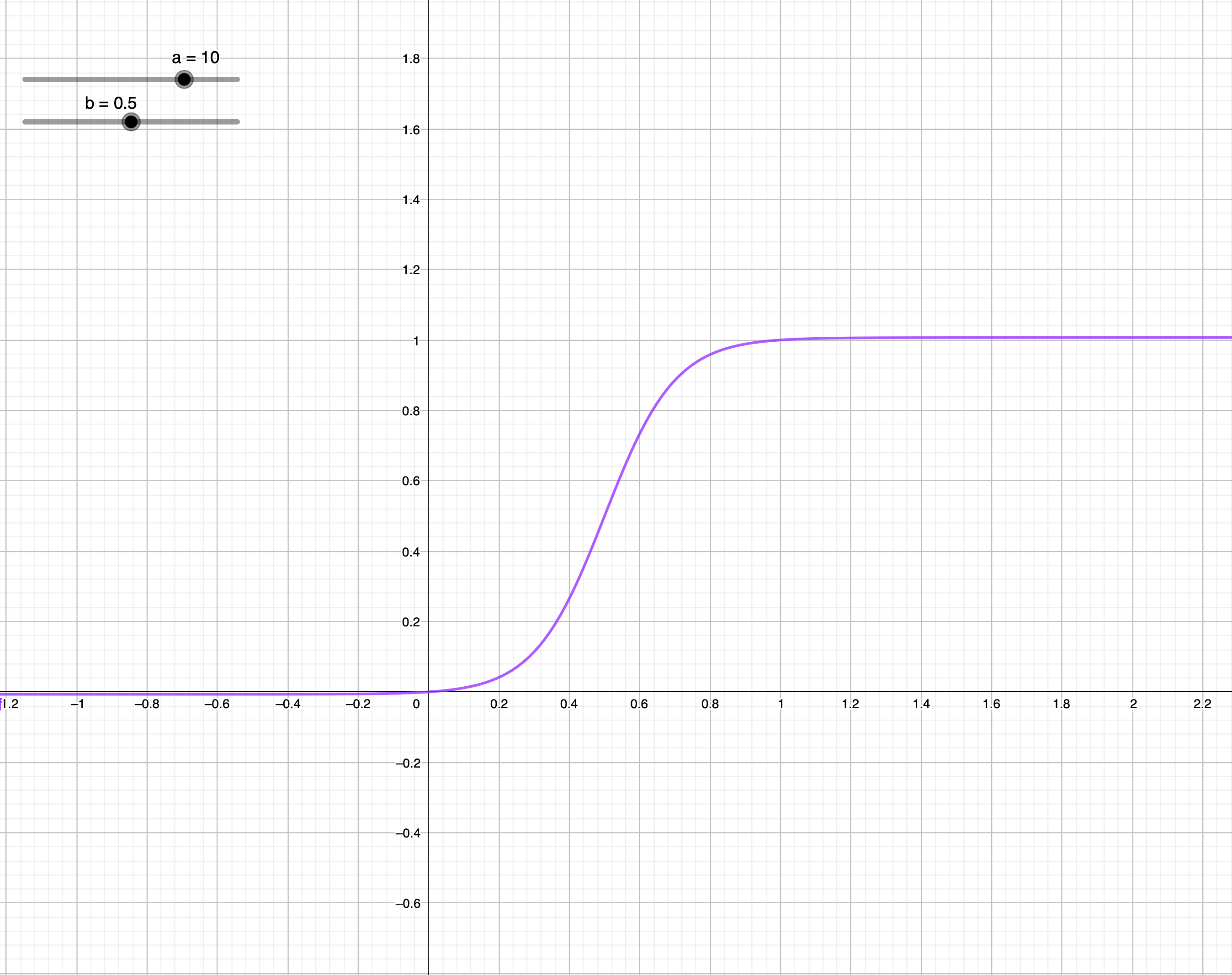
いいところ
- 滑らか
- ナイーブ
悪いところ
- コントラスト下げる方には対応できなさそう
- と思ったら『ガンマ曲線とシグモイド曲線による画像補正』ではできてるっぽい。どうして。。。
2. PseudoSigmoid
『シグモイド曲線の定義域が有界でないので、有界なシグモイド曲線を勝手に作ってみた』の実装
f(x) = \frac{sinh^{−1}[(2x−1)sinh(t)]}{2t} + \frac{1}{2}
結果
https://www.geogebra.org/m/ubnfhnzn
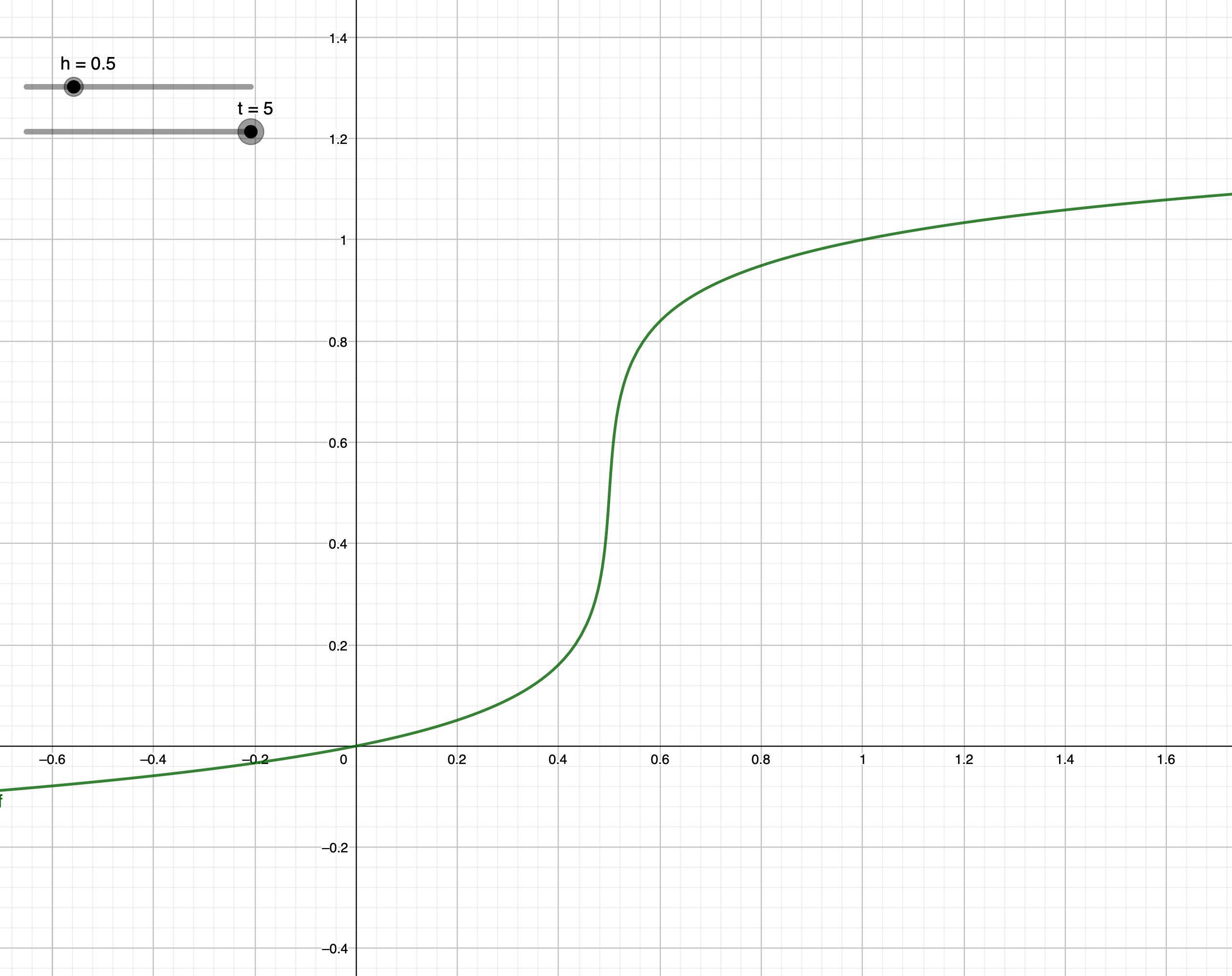
いいところ
- 綺麗
悪いところ
- 難しい
- コントラスト下げる方には対応できない
3. 指数アプローチ
指数で実装してみる。
$x^t$は$(0,0)$と$(1,1)$を通るので、これを二つひっくり返して繋げれば点対称なS字カーブができる。
以下$h$は変曲点。($[0,1]$にしたければ$h=0.5$)
f(x) = \left\{
\begin{array}{ll}
h \Big( 1 + \big( \frac{x-h}{h} \big)^{2^t} \Big) & (x \geq h) \\
h \Big( 1 - \big( \frac{h-x}{h} \big)^{2^t} \Big) & (x \lt h)
\end{array}
\right.
結果
https://www.geogebra.org/m/d4zzqtqy
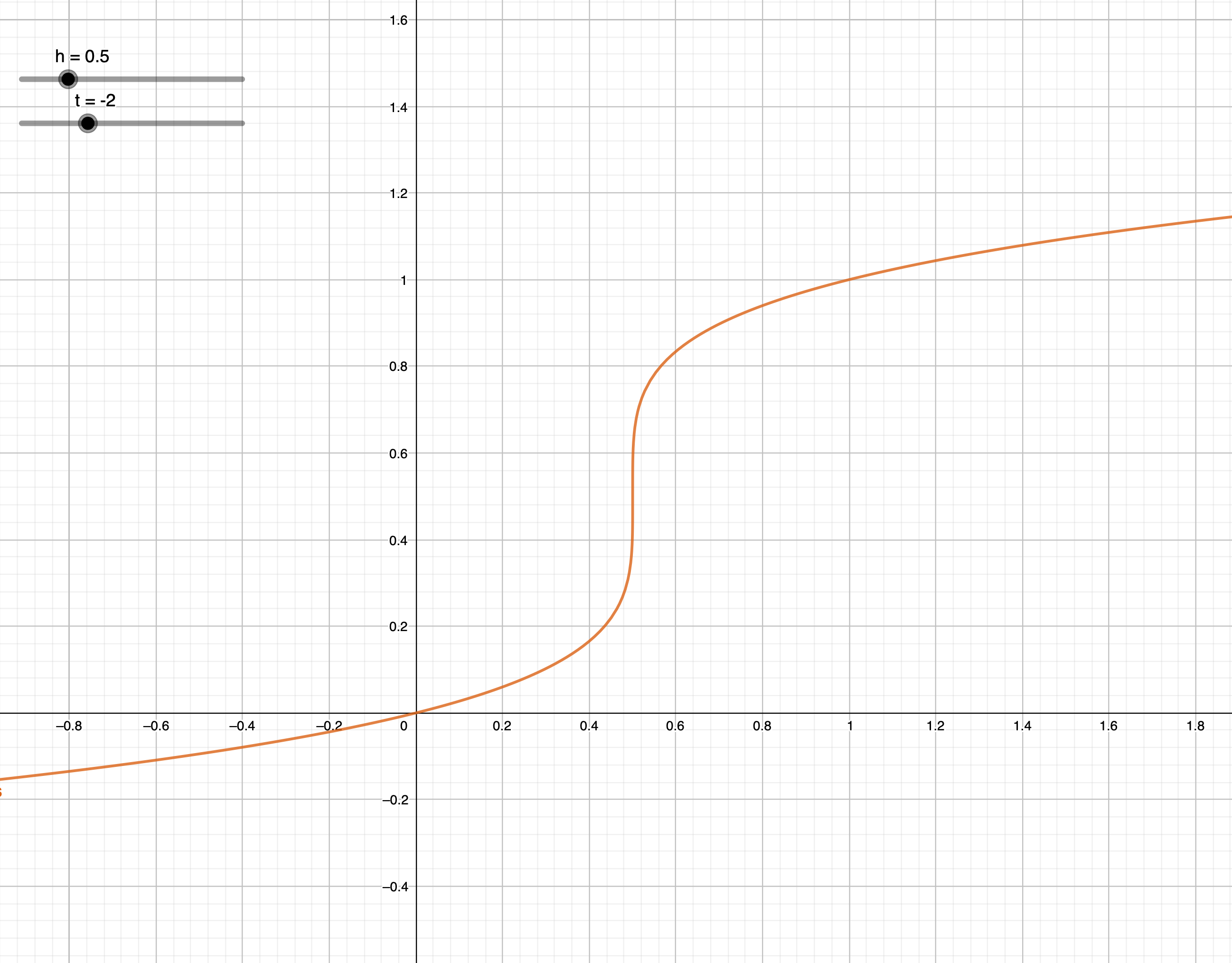
- なんかだいぶキモい
- pHジャンプだこれ
いいところ
- 負の値が実装できる
悪いところ
- 変曲点付近に張り付く
ここで気づく
f(x) = \frac{sinh^{−1}[(2x−1)sinh(t)]}{2t} + \frac{1}{2}
これ、逆関数出せるのでは?
4. 拡張PseudoSigmoid
$t$が負の時には逆関数に移行することで、コントラストを落とす方にも対応する
f(x) = \left\{
\begin{array}{ll}
0 & (t = 0)\\
\frac{sinh^{−1}[(2x−1)sinh(t)]}{2t} + \frac{1}{2} & (t \gt 0) \\
\frac{sinh[(2x−1)t]}{2sinh(t)} + \frac{1}{2} & (t \lt 0)
\end{array}
\right.
結果
https://www.geogebra.org/m/fxfwepyu

実装
そのまま書いてみた ($[0,MAX] \rightarrow [0,MAX]$)
extended_pseudosigmoid.js
function extended_pseudosigmoid(x, t, MAX){
if (t === 0) return x;
else if (t > 0) return (Math.asinh((2 * x / MAX - 1) * Math.sinh(t)) / 2 / t + 0.5) * MAX;
else return (Math.sinh(t * (2 * x / MAX - 1)) / 2 / Math.sinh(t) + 0.5) * MAX;
};
結論
$\star$Sigmoidは偉大––––––!