Wikipedia - シグモイド
タイトルの通り、シグモイド曲線の定義域は $(-\infty,\ +\infty)$ と有界ではありません。
これでは計算機で取り扱う時、閉区間でないことが原因でぴったりした値を出せないため、中途半端な値を相手にプログラミングしなければなりません。
もっと厳密に結果を出したい!ということで、同じような曲線を描く、定義域も値域も閉区間な関数を勝手に作っちゃいましょう。
PseudoSig_{t}(x)\ =\ \frac{\sinh^{-1} [ (2x-1) \sinh(t) ] }{2t}\ + \ \frac{1}{2}
次の図は $t = 4$ とした時に出力した図です。
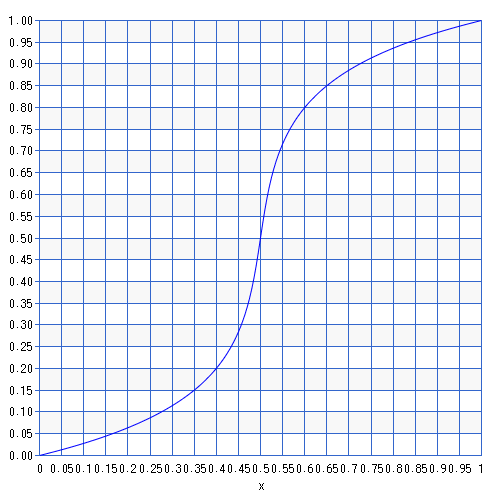
一般に、 $t$ を大きくすると曲がり具合が強くなります。
今回の例では $\frac{1}{2}$ を足すことで値域を $[0,\ 1]$ にしましたが、この項を消すことで通常のシグモイド曲線の様に変形することが可能です。
謝辞
図の出力には以下のサイトを用いました。
http://keisan.casio.jp