以前に因果推論についての記事を書きましたが、因果推論は説明できても因果関係とは何ぞやとなった場合に意外と説明できない方も多いのではないでしょうか。
因果関係は様々な考え方がありますが、ここでは「疫学」における因果関係について説明していこうと思います。
疫学と聞くと疫病を未然に防ぐ医学の学問と思われがちですが、実際には統計学に近い学問で、統計学はデータ分析とすると疫学はデータの集め方とググったら出てきます。
例えば因果関係を推定するためにデータを集めるには

ランダム化比較試験(RCT)
ある試験的操作（介入・治療など）を行うこと以外は公平になるように，対象の集団(特定の疾患患者など)を無作為に複数の群（介入群と対照群や，通常＋新治療を行う群と通常の治療のみの群など）に分け，その試験的操作の影響・効果を測定し，明らかにするための比較研究
(出典：日本理学療法学会連合)
コホート研究
ある特定の疾患の起こる可能性がある要因・特性を考え，対象集団（コホート）を決め，その要因・特性を持った群（曝露群）と持たない群（非曝露群）に分け，疾患の罹患や改善・悪化の有無などを一定期間観察し，その要因・特性と疾患との関連性を明らかにする研究方法
(出典：日本理学療法学会連合)
症例対象研究
ある疾患をもつ患者群とそれと比較する対照群に分けて，疾患の特徴や疾患の起こる可能性がある要因にさらされているかどうか，また背景因子の違いなどを比較し，関連を確認するための研究方法
(出典：日本理学療法学会連合)

等が因果関係を推定する上で使われる疫学研究に基づくデータ収集方法です。
ここでRCTの説明であった「その試験的操作の影響・効果を測定し」から分かる通り過去に書きましたこちらの記事も因果関係を推定する一つの手法になります。

では、ここから本題で、因果関係は疫学ではどう考えているかについて触れていきます。
出典は『基礎から学ぶ楽しい疫学第4版』です。

時間的関係
曝露と、これに続いて(時間的には後に)起こる疾病発生の時間的関係がきちんと確認されないと両者に因果関係があるとは言えない
一致性
種々の状況における研究で曝露と疾病発生の間に同様の関連が観察される事
強固性
相対危険が大きいほど高くなる
量反応関係
曝露(量、時間、量×時間)が増加するにつれて相対危険が大きくなる事
整合性
観察された関連が疫学以外の知見と矛盾しない事

このほかに必要条件と十分条件もありますが、今回は省略します。
では、この中でプログラム的に定量的に算出できるものとしては「強固性」と「量反応関係」があります。
ここで、「量反応関係」について「相対危険」という言葉が使われていますが、出典に使用している書籍ではオッズ比が使われており、そこから分かる通りロジスティック回帰が使用されています。
ではこの2点について実際にプログラムで考えてみましょう。

ライブラリ

import statsmodels.api as sm
import pandas as pd
import numpy as np

データの読み込み

df = pd.read_csv("leukemia.csv")
df.head()

強固性

ここではリスク比としてRx(投与)にの有無に対しstatus(効果)の有無のにどのような違いが現れるかを測定します。

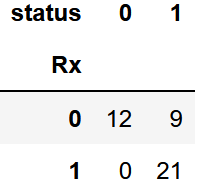
クロス集計表

crs = pd.crosstab(df["Rx"], df["status"])
crs

結果、以下のようなクロス集計表が現れます。

リスク比の算出

次にここからリスク比を算出します。リスク比の算出にはまずリスク(原因の事象に対する結果の事象の割合)を計算して、リスクを除算します。

ary = crs.values
risk = [ary[0][1]/sum(ary[0]), ary[1][1]/sum(ary[1])]
df_risk = pd.DataFrame(risk)
df_risk.columns = ["risk"]
crs = pd.concat([crs, df_risk], axis=1)
df_rr = pd.DataFrame(["NaN", risk[1]/risk[0]])
df_rr.columns = ["risk_rate"]
crs = pd.concat([crs, df_rr], axis=1)
crs

この結果以下のようにリスク比が算出されます。

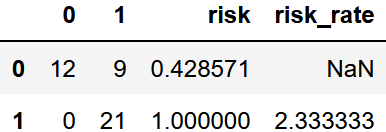
解釈としては投与した人は投与していない人に比べて約2.3倍効果が現れる事が分かります。

量反応関係

先述した通り、量反応関係にはロジスティック回帰を用いて、その後回帰係数をオッズ比にします。なお、ここでは量的変数に着目するため質的変数は除きます。そのため、白血球数と時間に着目します。

y = df["status"]
x = sm.add_constant(df.drop(["status", "sex", "Rx"], axis=1))
model = sm.Logit(y, x).fit_regularized()
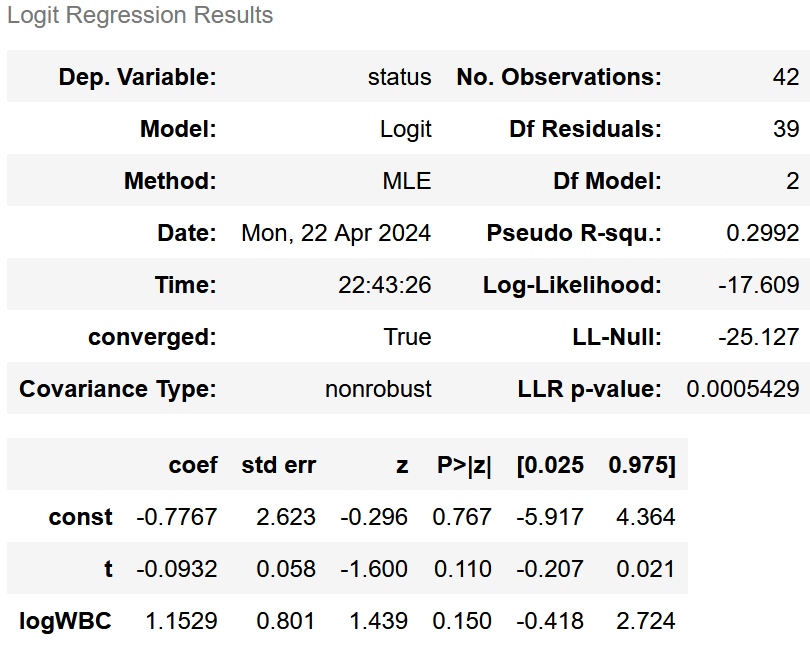
model.summary()

オッズ比の算出

オッズ比は自然対数に係数乗することで算出できます。

prms = []
for i in range(len(model.params)):
    prms.append([x.columns[i], np.exp(model.params[i])])
df_odds = pd.DataFrame(prms)
df_odds.columns = ["coef", "odds_ratio"]
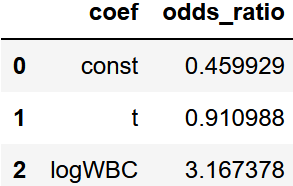
df_odds

オッズ比の解釈としては、オッズ比の値が大きいほどデータの数が大きい時に陽性(反応)になりやすいという事になります。
そのため、ここではlogWBCが大きいほど陽性になりやすいということが分かります。

まとめ

ここまで見てみると相関関係と因果関係では全く分析方法が異なり、そもそも因果関係はデータの集め方から考えて集める時点でお金も時間もかかり、なおかつ様々な指標があるため因果関係を認めることは難しいことが分かるのではないかと思います。

参考文献

ランダム化比較試験（RCT）　randomized controlled trial - 一般社団法人日本理学療法学会連合
 コホート研究　cohort study - 一般社団法人日本理学療法学会連合
 症例対照研究　case control study - 一般社団法人日本理学療法学会連合
 基礎から学ぶ楽しい疫学第4版 | 中村好一

因果関係の考え方