基本式「y=wTx」
こんにちは、mucunです。
今回は、機械学習の基本式「$y=w^Tx$」の紹介をした上で、
MATLABでの簡易の機械学習方法について紹介したいと思います。
前回の記事では、以下内容の話をさせてもらいました。
- 識別のための「重み」を算出するのことが「機械学習」
- 「重み」を算出すれば、未知のデータで予測ができる
しかし、うーん、、、
文章の説明を見返すと、何だか分かりづらいですね。
ですが、これ、数式で表現すると非常に分かりやすくなります。
数式で、機械学習を説明する
先に言っておくと「$y=w^Tx$」で表現される機械学習手法は、
最も基本となる単純な手法となります。
ただ、全ての機械学習はこの式の応用で表現できますので、
先ずは基本を押させておきましょう。
機械学習手法基本の登場人物についてまとめると、
- $x_{known}$ : 結果が既知の学習用データ
- $y_{known}$ : 学習用データに結びつく何かしらの結果
- $w$ : 学習サンプルデータとその結果から算出した重み
- $x_{unknown}$ : 結果が未知のデータ
- $y_{forecast}$ : 結果が未知のデータの予測結果
以上、5つです。
この登場人物と数式を用いて、機械学習の説明をすると、
機械学習とは、
$y_{known}=w^Tx_{known}$
が成立する「$w$」を算出し、算出した「$w$」を用いて、
$y_{forecast}=w^Tx_{unknown}$
という計算を行い、予測を実施する。
となります。
どうですか?
分かりやすくないですか?
データの性質を確認
ここで、登場人物のデータの性質を確認します。
- $x_{known}$ : 特徴次元「$d$」×学習用サンプル数「$n_{known}$」の行列
- $y_{known}$ : 学習用サンプル数「$n_{known}$」のベクトル
- $w$ : 特徴次元「$d$」のベクトル
- $x_{unknown}$ : 特徴次元「$d$」×未知のサンプル数「$n_{unknown}$」の行列
- $y_{forecast}$ : 未知のサンプル数「$n_{unknown}$」のベクトル
以上です。
未知のサンプル何れについても、共通の重み「$w$」を掛け合わせることで、
予測が実施できるという訳です。
基本原理を知らなくても、とりあえず「w」を求める方法
「$w$」を算出する際の基本的な概念は、
学習用サンプルにおいて、「$y_{known}$」と「$w^Tx_{known}$」の差が、
最も小さくなるように「$w$」を求めるというものです。
(※「$y_{known}$」と「$w^Tx_{known}$」は、基本的には一致しません)
差分を最小化するためには、少し込み入った処理が必要なのですが、
実は、MATLABを使えば簡単に「$w$」を求めることができます。
それを実現しているMATLABコードが以下です。
clear all;
rng(0);
% make data
n_sample = 50;
d = 30;
x_sample = randn(d, n_sample);
y_sample = randn(1, n_sample);
% solve weight
w = (y_sample / x_sample)';
% check result
y_approach = w' * x_sample;
figure;
plot(y_sample, '--r', 'linewidth', 2); grid on; hold on;
plot(y_approach, '-b', 'linewidth', 2);
legend({'y\_sample', 'y\_approach'});
ここで行っていることは、
$y_{sample}=w^Tx_{sample}$
という式を変形して、
$y_{sample}/x_{sample}=w^T$
$(y_{sample}/x_{sample})^T=w$
$w=(y_{sample}/x_{sample})^T$
として、「$w$」を求めてしまおう、というものです。
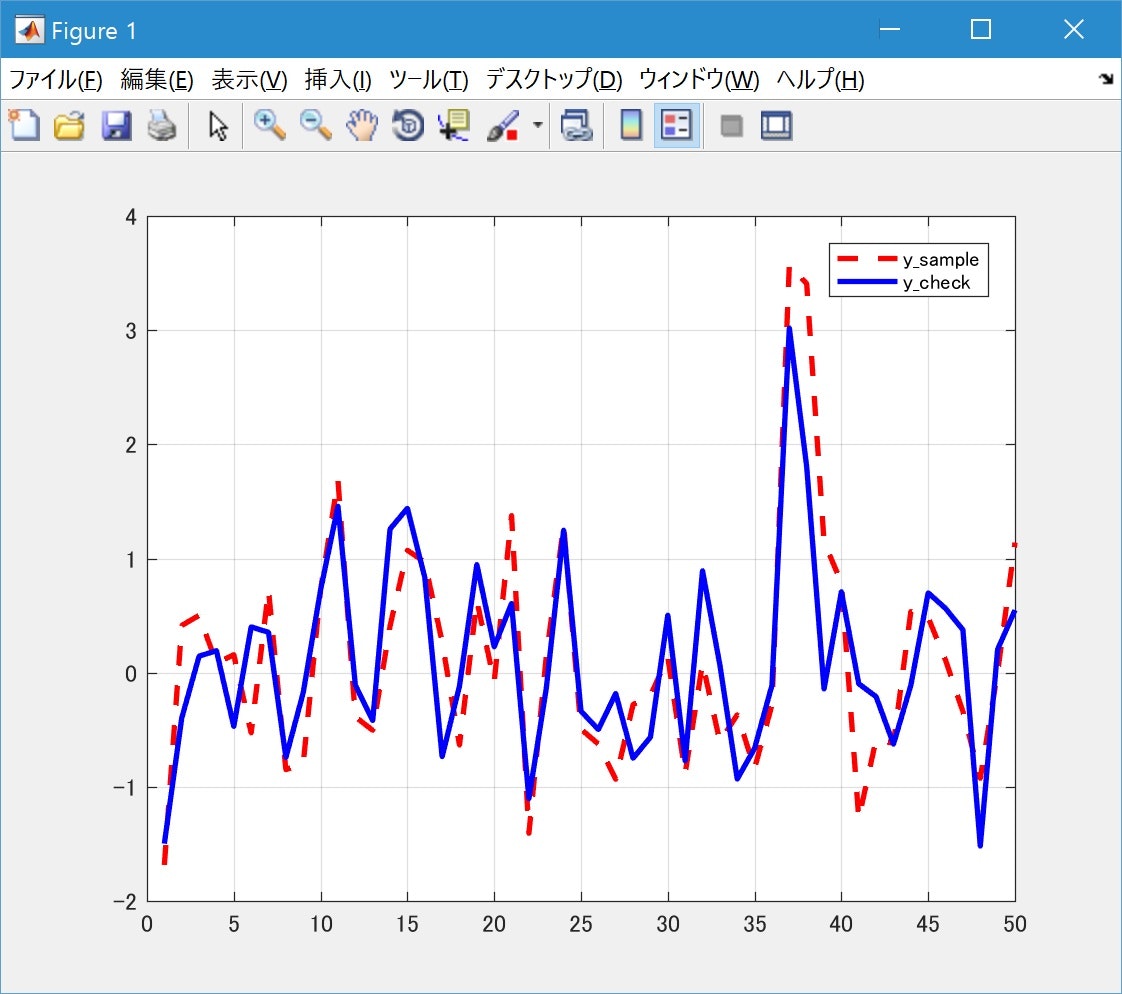
プロットは、正解値の「$y_{sample}$」と、
求めた「$w$」から「$w^Tx_{sample}$」を計算した「$y_{approach}$」との比較です。
パッと見、結果ベースで割とフィッティングできている気がします。
ここで「$x_{sample}$」は行列なので、
本来、単純に両辺を割ることができないのですが、
そこは MATLABが上手いこと解釈してくれるので、
上記のような行列での割り算ができてしまいます。
どんな解釈をしてくれているかは、次回以降詳しく説明をします。
今回の記事はここまでとなります。
読んで下さった方、ありがとうございました。('◇')ゞ