この記事は、私が参加しているオンラインセミナー「統計検定準一級勉強会」の講義ノートです。セミナーで使用しているテキスト「統計学実践ワークブック」は統計学のエッセンスを簡潔にまとめている良書ですが、数式などは結果のみで導出方法が記載されていないので、この記事で、できるだけフォローしました。このテキストを使用して勉強している人の理解の手助けに少しでもなれば幸いです。間違いや助言があればご指摘していただくとありがたいです。
$$
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
$$
23 判別分析(その1)
フィッシャーの判別分析
ここでは、テキストP.203~P.204に沿って、フィッシャーの線形判別関数の導出を行います。テキストには
ベクトル $\boldsymbol{w} \in \mathbb{R}^{p}$ による射影を考え、射影後のサンプルを
$$y_{i}^{(j)}
= \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}^{(j)},\quad j=1,2,\quad i=1,\cdots,n_j
\quad・・・\quad(1)
$$とする。
と書いてありますが、これを幾何学的に説明したものが Fig.1(左側)です。テキストには明示的に書いてはいませんが、$\boldsymbol{w}$ は単位ベクトルです($|\boldsymbol{w}|=1$)。
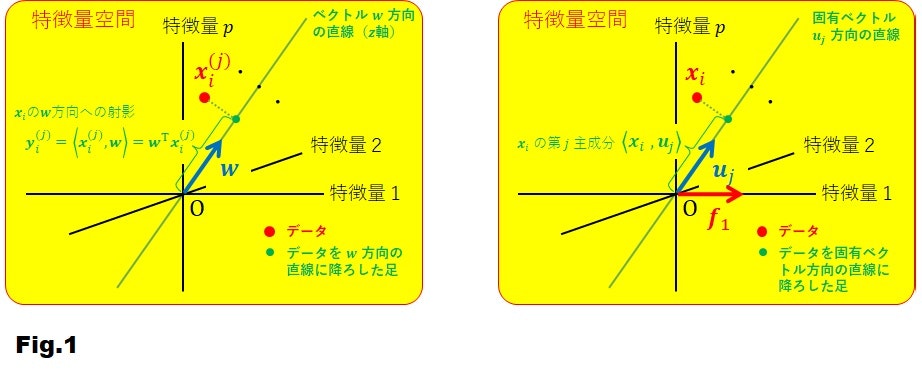
$y_{i}^{(j)}$ は、$G_j$ 群に属する観測データ $\boldsymbol{x}_{i}^{(j)}$ の、あるベクトル $\boldsymbol{w}$ 方向の直線(これを $z$ 軸とよぶ)への正射影です。これは、Fig.1(右側)に示した主成分分析の主成分に似ていますね。主成分分析の場合は、観測データ $\boldsymbol{x}_i$ は、固有ベクトル $\boldsymbol{u}_j$ 方向の直線への正射影が主成分でした。そして、ベクトル $\boldsymbol{u}_1$ は、($j$=1 すなわち第1主成分の場合)、観測データの主成分の分散が最大(つまり、観測データの広がり具合が最大)になるように選びました。では、判別分析の $\boldsymbol{w}$ はどうやって決めるのでしょうか。
それを模式的に示したのが Fig.2 です。この図は、観測するデータ群 $G_j, j=1,2$ と $\boldsymbol{w}$ 方向の直線 $z$ 軸を描いたものです。
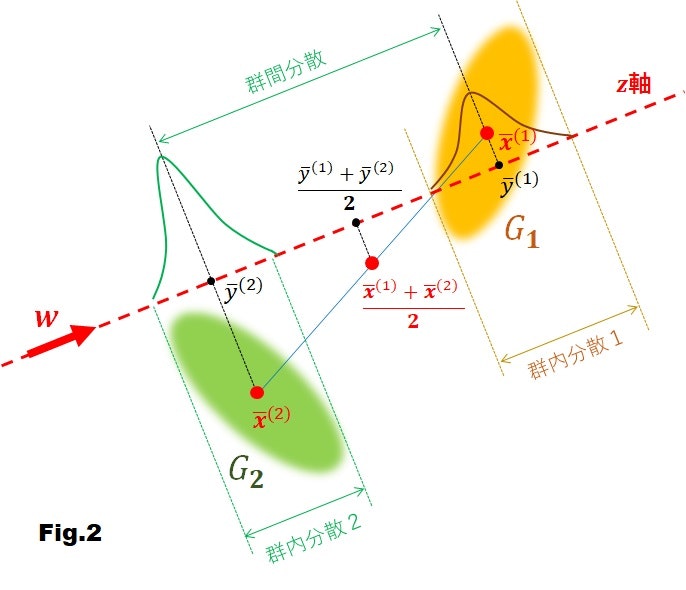
図中の $\bar{\boldsymbol{x}}^{(1)}, \bar{\boldsymbol{x}}^{(2)}$ は、それぞれ群 $G_1, G_2$ の標本平均で
$$
\bar{\boldsymbol{x}}^{(j)} = \frac{1}{n_j}\sum_{i=1}^{n_j}\boldsymbol{x}_{i}^{(j)},\quad j=1,2\quad・・・\quad(2)
$$
です。また、$\bar{y}^{1},\bar{y}^{2}$ は、それぞれ $\bar{\boldsymbol{x}}^{(1)}, \bar{\boldsymbol{x}}^{(2)}$ から $z$ 軸に下ろした足(正射影)で
$$
\bar{y}^{(j)} = \frac{1}{n_j}\sum_{i=1}^{n_j}y_{i}^{(j)}
=\frac{1}{n_j}\sum_{i=1}^{n_j}\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}^{(j)}=\boldsymbol{w}^{\mathrm{T}}\bar{\boldsymbol{x}}^{(j)}
,\quad j=1,2\quad・・・\quad(3)
$$
です。ここで、第2項から第3項へ移るときに(1)式を、第3項から第4項へ移るとき
に(2)式を使いました。
さて、$\boldsymbol{w}$ をどうやって決めるかですが、判別分析の目的は、任意の観測 $\boldsymbol{x}$ が、群 $G_1$ と $G_2$ のどちらに帰属するかを判別することなので、できるだけ群 $G_1$ と $G_2$ の間が離れていて、かつ、できるだけ各々の群内の広がりが小さく見えるような射影軸である $z$ 軸(したがってベクトル $\boldsymbol{w}$ の方向)を選ぶことが基準になります。それを定式化すると
$$
\boldsymbol{\hat{w}}=\argmax_{\boldsymbol{w}}\hspace{3pt}\lambda(\boldsymbol{w})\quad・・・\quad(4)
$$
です。ここで、$\lambda(\boldsymbol{w})$ は、テキストP.204の4行目にある
$$ \lambda(\boldsymbol{w})=\frac{群間分散}{群内分散} \quad・・・\quad(5)$$
です。
群間分散といっても、この場合群は、$G_1$ と $G_2$ のたった2つしかないので、射影 $\bar{y}^{(1)}$ と $\bar{y}^{(2)}$ の距離の2乗として定義します。すなわち
$$
\begin{eqnarray}
群間分散 \triangleq \left(\bar{y}^{(1)}-\bar{y}^{(2)}\right)^2
&=& \left(\boldsymbol{w}^{\mathrm{T}}\bar{\boldsymbol{x}}^{(1)}-\boldsymbol{w}^{\mathrm{T}}\bar{\boldsymbol{x}}^{(2)}\right)^2 \\
&=&\left[\boldsymbol{w}^{\mathrm{T}}\left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2\quad・・・\quad(6)
\end{eqnarray}
$$
となります。ここで、1行目の式変形のときに(3)式を使いました。
次に群内分散です。群 $G_j,\hspace{3pt}j=1,2$ の群内分散は、次のように求めることができます。
$$
\begin{eqnarray}
群 G_j の群内分散
&\triangleq& \frac{1}{n_{j}-1}\sum_{i=1}^{n_j}\left(y_{i}^{(j)}-\bar{y}^{(j)}\right)^{2} \\
&=& \frac{1}{n_{j}-1} \sum_{i=1}^{n_{j}} \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}^{(j)}-\boldsymbol{w}^{\mathrm{T}}\bar{\boldsymbol{x}}^{(j)}\right)^{2} \\
&=& \frac{1}{n_j-1} \sum _{i=1}^{n _{j}} \left[\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\right]^{2} \\
&=& \frac{1}{n_j-1} \sum _{i=1}^{n _{j}}\left[\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\right]\left[\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\right] \\
&=& \frac{1}{n_j-1} \sum _{i=1}^{n _{j}}\left[\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\right]\left[\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)^{\mathrm{T}}\boldsymbol{w}\right] \\
&=& \frac{1}{n_j-1} \sum _{i=1}^{n _{j}}\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)^{\mathrm{T}}\boldsymbol{w} \\
&=& \boldsymbol{w}^{\mathrm{T}}\left[\frac{1}{n_j-1} \sum _{i=1}^{n _{j}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)^{\mathrm{T}}\right]\boldsymbol{w} \\
&=& \boldsymbol{w}^{\mathrm{T}}S_j\boldsymbol{w}\quad・・・\quad(7)
\end{eqnarray}
$$
ここで、4行目から5行目へ式変形するとき、2つのベクトル $\boldsymbol{a},\boldsymbol{b}$ の内積はスカラーなので、転置しても変わらないという性質 $\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}=\left(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}\right)^{\mathrm{T}}=\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}$ を利用しています。また、5行目から6行目へ式変形するとき、$\left(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}\right)\left(\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}\right)=\boldsymbol{a}^{\mathrm{T}}\left(\boldsymbol{b}\boldsymbol{b}^{\mathrm{T}}\right)\boldsymbol{a}$ という恒等式を利用しました。
参考のために、証明を以下に書いておきます。
- $\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}=\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}$ の証明
$$
\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}=\sum_{i}a_{i}b_{i},\quad \boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}=\sum_{i}b_{i}a_{i} \quad \Longrightarrow \quad \boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}=\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a} \quad・・・\quad(8)
$$
- $\left(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}\right)\left(\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}\right)=\boldsymbol{a}^{\mathrm{T}}\left(\boldsymbol{b}\boldsymbol{b}^{\mathrm{T}}\right)\boldsymbol{a}$ の証明
$$
\begin{eqnarray}
\left(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{b}\right)\left(\boldsymbol{b}^{\mathrm{T}}\boldsymbol{a}\right)
&=&\sum_{i}a_{i}b_{i} \sum_{j}b_{j}a_{j} \\
&=& \sum_{i}a_{i} \sum_{j}b_{i}b_{j}a_{j} \\
&=& \sum_{i}a_{i}\sum_{j}\left(\boldsymbol{b}\boldsymbol{b}^{\mathrm{T}}\right)_{ij}a_j \\&=& \sum_i a_i \left(\left(\boldsymbol{b}\boldsymbol{b}^{\mathrm{T}}\right)\boldsymbol{a}\right)_i \\ &=& \boldsymbol{a}^{\mathrm{T}} \left( \boldsymbol{b}\boldsymbol{b}^{\mathrm{T}}\right) \boldsymbol{a} \quad・・・\quad(9)
\end{eqnarray}
$$
なお、(7)式の最後の行に出てくる $S_j$ は群 $G_j$ に含まれるサンプル $\lbrace\boldsymbol{x}_{i}^{(j)}\rbrace _{i=1}^{n_j}$ の標本分散共分散行列で、次式で定義されます。
$$
S_j = \frac{1}{n_j-1} \sum _{i=1}^{n _{j}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)^{\mathrm{T}} \quad・・・\quad(10)
$$
こうして、群 $G_j$ の群内分散を求めることができたので、全体の群内分散を考えてみましょう。群 $G_j$ の標本分散共分散行列は、(10)式のように偏差二乗和(サンプルの平均からの距離の二乗和)をデータの自由度(データ数から1を引いた数値)で割っています。したがって、自然な拡張として、全体の標本分散共分散行列 $S$ は次式で定義できるのではないでしょうか。
$$
\begin{eqnarray}
S
&=& \frac{1}{n_1+n_2-2} \sum _{j=1}^{2} \sum _{i=1}^{n _{j}}\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)\left(\boldsymbol{x}_i^{(j)}-\bar{\boldsymbol{x}}^{(j)}\right)^{\mathrm{T}} \\
&=& \frac{1}{n_1+n_2-2} \sum _{j=1}^{2} (n_j-1)S_j \quad・・・\quad(11)
\end{eqnarray}
$$
ここで、2行目に移るとき(10)式を用いました。また、$n_1+n_2-2$ はデータの自由度です。(11)式で与えられる全体の標本分散共分散行列を用いて全体の群内分散を次のように定義できます。
$$
全体の群内分散=\boldsymbol{w}^{\mathrm{T}}S\boldsymbol{w}\quad・・・\quad(12)
$$
(6)式と(12)式を(5)式に代入すると、次式を得ます。
$$
\lambda(\boldsymbol{w}) = \frac{\left[\boldsymbol{w}^{\mathrm{T}}\left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}{\boldsymbol{w}^{\mathrm{T}}S\boldsymbol{w}}
\quad・・・\quad(13)
$$
したがって、$\boldsymbol{w}$ を求める問題は(4)式から次式のように定式化できます。
$$
\boldsymbol{\hat{w}} = \argmax_{\boldsymbol{w}}\hspace{3pt} \frac{\left[\boldsymbol{w}^{\mathrm{T}}\left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}{\boldsymbol{w}^{\mathrm{T}}S\boldsymbol{w}} \quad \mathrm{with} \quad 制約条件 \hspace{4pt} |\boldsymbol{w}| = 1 \quad・・・\quad(14)
$$
こういった極値問題はラグランジュの未定乗数法で解くことができます。ラグランジュの未定乗数を $\kappa$ とし、ラグランジュ関数を次式で定義します。
$$
L(\boldsymbol{w},\kappa) = \frac{\left[\boldsymbol{w}^{\mathrm{T}}\left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}{\boldsymbol{w}^{\mathrm{T}}S\boldsymbol{w}} - \kappa \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w} - 1\right) \quad・・・\quad(15)
$$
ここで、制約条件 $|\boldsymbol{w}|=1$ は、計算を簡単にするため、同等な制約条件 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w}=1$ としました。
したがって、
$$
\begin{eqnarray}
\frac{\partial L(\boldsymbol{w},\kappa)}{\partial \boldsymbol{w}} &=& 0 \quad・・・\quad(16) \\
\frac{\partial L(\boldsymbol{w},\kappa)}{\partial \kappa} &=& 0 \quad・・・\quad(17) \\
\end{eqnarray}
$$
という停留値問題を解けば(14)式の最適解 $\boldsymbol{\hat{w}}$ を得ることができます。まず、計算を簡単にするために $\boldsymbol{a} = \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}$ とおくと、(16)式は
$$
\begin{eqnarray}
\frac{\partial L(\boldsymbol{w},\kappa)}{\partial \boldsymbol{w}}
&=& \frac{\partial}{\partial \boldsymbol{w}} \frac{\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2}}{\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}} \\
&=& \frac{\frac{\partial \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2}}{\partial \boldsymbol{w}}\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)-\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2} \frac{\partial \left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)}{\partial \boldsymbol{w}}}{\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)^2} = 0
\quad・・・\quad(18) \\
\end{eqnarray}
$$
ですから、
$$
\frac{\partial \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2}}{\partial \boldsymbol{w}}\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)-\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2} \frac{\partial \left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)}{\partial \boldsymbol{w}} = 0
\quad・・・\quad(19)
$$
が得られます。
ここで、
$$
\begin{eqnarray}
\frac{\partial \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2}}{\partial \boldsymbol{w}}
= 2\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) \frac{\partial \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)}{\partial \boldsymbol{w}}
= 2\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) \boldsymbol{a}
\quad・・・\quad(20) \\
\frac{\partial \left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)}{\partial \boldsymbol{w}}
= \left(S+S^{\mathrm{T}}\right) \boldsymbol{w} = 2S \boldsymbol{w}
\quad・・・\quad(21)
\end{eqnarray}
$$
なので、これらを(19)式に代入すると
$$
2\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) \boldsymbol{a}\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right)-\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)^{2} 2S\boldsymbol{w}
= 2\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right)
\lbrace
\boldsymbol{a}\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right) - \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) S\boldsymbol{w}
\rbrace
= 0
\quad・・・\quad(22)
$$
となるので、最終的に
$$
\boldsymbol{a}\left(\boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}\right) = \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) S\boldsymbol{w}
\quad・・・\quad(23)
$$
が得られます。
(23)式に $S\boldsymbol{w} = \boldsymbol{a}$ を代入すると $\boldsymbol{a}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{a}\right) = \left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}\right) \boldsymbol{a}$ となり、$\boldsymbol{w}^{\mathrm{T}}\boldsymbol{a}$ はスカラーであることに注意すると、これは恒等的に成立するので
$$
\hat{\boldsymbol{w}} = S^{-1} \boldsymbol{a} = S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)
\quad・・・\quad(24)
$$
が得られます。
フィッシャーの線形判別関数
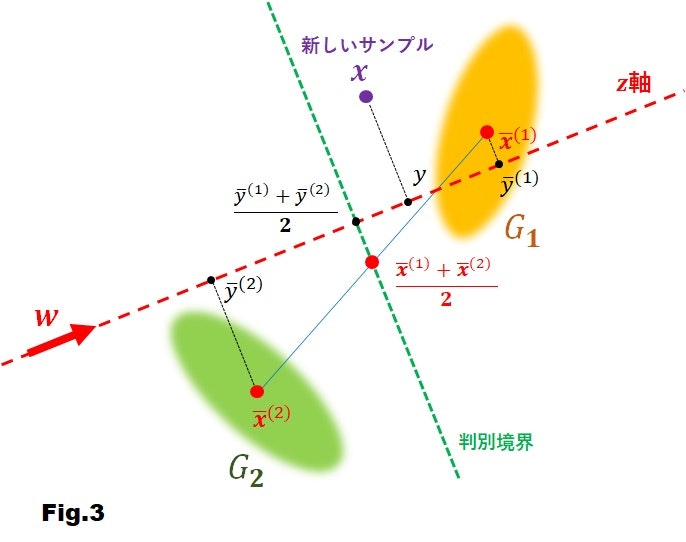
さて、Fig.3のように、新しいサンプル $\boldsymbol{x}$ が与えられたとき、これは群 $G_1, G_2$ のどちらに属するでしょうか?
テキストには、次のように書かれています。
新しいサンプル $\boldsymbol{x}$ は $y = \hat{\boldsymbol{w}}^{\mathrm{T}}\boldsymbol{x}$ のように射影される。このサンプルがどちらの群に属するかを定めるには、射影後の各群に属する標本平均を求め、その中点 $\left( \boldsymbol{w} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(1)} + \boldsymbol{w} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(1)} \right) / 2
= \left( \bar{\boldsymbol{x}} ^{(1)} - \bar{\boldsymbol{x}} ^{(2)}\right)^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}} ^{(1)} - \bar{\boldsymbol{x}} ^{(2)} \right) / 2$ と $y$ を比較すればよい。
ここで、最後の式展開について確認してみましょう。Fig.3に示すように、$\frac{1}{2} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right)$ の射影後の中点は $\frac{1}{2} \left( \bar{y} ^{(1)} + \bar{y} ^{(2)} \right)$ です。したがって
$$
\begin{eqnarray}
\frac{1}{2} \left( \bar{y} ^{(1)} + \bar{y} ^{(2)} \right)
&=& \frac{1}{2} \left( \hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(1)} + \hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \frac{1}{2} \hat{\boldsymbol{w}} ^{\mathrm{T}} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \frac{1}{2} \left[ S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) \right] ^{\mathrm{T}} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \frac{1}{2} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} \left( S^{-1} \right) ^{\mathrm{T}} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \frac{1}{2} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right)
\quad・・・\quad(25)
\end{eqnarray}
$$
となります。ここで、2行目から3行目に移るときに(24)式を、4行目から5行目に移るときに $\left( S^{-1} \right) ^{\mathrm{T}} = S^{-1}$ を用いました。
【 $\left( S^{-1} \right) ^{\mathrm{T}} = S^{-1}$ の証明 】
共通の標本分散共分散行列 $S$ は対称行列なので $S^{\mathrm{T}} = S$ である。また $SS^{-1} = I$ であるから両辺の転置をとると $\left( SS^{-1} \right) ^{\mathrm{T}} = I$ となり、これは $\left( S^{-1} \right) ^{\mathrm{T}} S^{\mathrm{T}} = I$ であるから、両辺の右から $\left( S^{\mathrm{T}} \right) ^{-1}$ を作用させると $\left( S^{-1} \right) ^{\mathrm{T}} = \left( S^{\mathrm{T}} \right) ^{-1} = S^{-1}$ となる。
したがって、判別関数 $f(\boldsymbol{x})$ は
$$
\begin{eqnarray}
f(\boldsymbol{x})
&=& y - \frac{1}{2} \left( \bar{y} ^{(1)} + \bar{y} ^{(2)} \right) \\
&=& \hat{\boldsymbol{w}}^{\mathrm{T}}\boldsymbol{x} - \frac{1}{2} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right)
\quad・・・\quad(26)
\end{eqnarray}
$$
となります。この判別関数をフィッシャーの線形判別関数といいます。この判別関数を用いると、新しいサンプル $\boldsymbol{x}$ が属する群は、次の規則に従います。
$$
\boldsymbol{x} の属する群 =
\begin{cases}
G_1 & ( f(\boldsymbol{x}) \gt 0 ) \\
G_2 & ( f(\boldsymbol{x}) \lt 0 )
\end{cases}
\quad・・・\quad(27)
$$
また、判別境界は中点 $ \frac{1}{2} \left( \bar{y} ^{(1)} + \bar{y} ^{(2)} \right)$ を通る $z$ 軸に直交する直線で、Fig.3において緑色の破線で示しています。
マハラノビス平方距離
(13)式に $\boldsymbol{w} = \hat{\boldsymbol{w}}$ を代入すると
$$
\begin{eqnarray}
\lambda(\hat{\boldsymbol{w}})
&=& \frac{\left[\hat{\boldsymbol{w}}^{\mathrm{T}}\left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}{\hat{\boldsymbol{w}}^{\mathrm{T}}S\hat{\boldsymbol{w}}} \\
&=& \frac
{\left[ \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)^{\mathrm{T}} S^{-1} \left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}
{\left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} SS^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)} \\
&=& \frac
{\left[ \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)^{\mathrm{T}} S^{-1} \left(\bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)}\right)\right]^2}
{\left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)} \\
&=& \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)
\quad・・・\quad(28)
\end{eqnarray}
$$
を得られます。ここで、(24)式と $\hat{\boldsymbol{w}} ^{\mathrm{T}} = \left[ S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) \right] ^{\mathrm{T}} = \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1}$ を用いました。この(28)式を $\bar{\boldsymbol{x}}^{(1)}$ と $\bar{\boldsymbol{x}}^{(2)}$ のマハラノビス平方距離とよび、$D^2$ で表記します。
$$
D^2
= \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right)
\quad・・・\quad(29)
$$
サンプル数に起因する判別関数の補正項
テキストP.205の冒頭には次のような記述があります。
群 $G_1, G_2$ に対する事象の生起確率が異なるときは、各群に属するデータが生じる事前確率 $\pi_1 = 1 - \pi_2$ を導入して $f(\boldsymbol{x}) - \log{(\pi_2 / \pi_1)} $ の正負を利用して判別を行うことができる。
この判別関数の補正項 $-\log{(\pi_2 / \pi_1)}$ はどこから出てくるのでしょうか?それを考察してみたいと思います2。
ベイズの定理をご存知でしょうか?ベイズの定理は、「事前確率(もともと持っている信念や考え)が尤度(新しいデータや経験)を受けて、どう変化するのかを示す事後確率を求めるための方法」です3。
判別分析でやりたいことは、新しいサンプル $\boldsymbol{x}$ が与えられたとき、それが群 $G_1, G_2$ のいずれに属するかを判定することです。これを数学的に定式化すると、
$$
\boldsymbol{x} の属する群 =
\begin{cases}
G_1 & ( P(G_1|\boldsymbol{x}) \gt P(G_2|\boldsymbol{x}) ) \\
G_2 & ( P(G_1|\boldsymbol{x}) \lt P(G_2|\boldsymbol{x}) )
\end{cases}
\quad・・・\quad(30)
$$
となります。ここで、$P(G_j|\boldsymbol{x})$ は、新しいサンプル $\boldsymbol{x}$ が与えられたとき、それが群 $G_j$ に属する条件付確率です。
ベイズの定理は、この条件付確率を求める公式で、次のように表されます。
$$
P(G_j|\boldsymbol{x}) = \frac{P(\boldsymbol{x}|G_j)P(G_j)}{P(\boldsymbol{x})}
\quad・・・\quad(31)
$$
ここで、$P(\boldsymbol{x}|G_j)$は、群が $G_j$ であるときに、サンプル $\boldsymbol{x}$ を観察する可能性(尤もらしさ)で、尤度とよびます。$P(G_j)$は、群 $G_j$ でデータ $\boldsymbol{x}$ が生起する確率で、事前確率とよびます。$P(\boldsymbol{x})$ は、データ $\boldsymbol{x}$ そのものを観察することの尤もらしさで、周辺尤度とよびます。そして、私たちが知りたい $P(G_j|\boldsymbol{x})$ を事後確率とよびます。ベイズの定理は、事前確率と尤度から事後確率を求める公式ということができます。
ここで、計算を簡単にするために、(31)式の両辺の対数をとってみましょう。すると、以下のようになります。
$$
\log{P(G_j|\boldsymbol{x})} = \log{P(\boldsymbol{x}|G_j)} + \log{P(G_j)} - \log{P(\boldsymbol{x})}
\quad・・・\quad(32)
$$
すると、(30)式で与えられる判別条件 $P(G_1|\boldsymbol{x}) \gt P(G_2|\boldsymbol{x})$ は、以下のような判別関数の正負の符号を評価することと同じになります。
$$
\begin{eqnarray}
f(\boldsymbol{x})
&=& \log{P(G_1|\boldsymbol{x})} - \log{P(G_2|\boldsymbol{x})} \\
&=& \lbrace \log{P(\boldsymbol{x}|G_1)} + \log{P(G_1)} - \log{P(\boldsymbol{x})} \rbrace - \lbrace \log{P(\boldsymbol{x}|G_2)} + \log{P(G_2)} - \log{P(\boldsymbol{x})} \rbrace \\
&=& \log{P(\boldsymbol{x}|G_{1})} - \log{P(\boldsymbol{x}|G_{2})} + \log{P(G_{1})} - \log{P(G_{2})} \\
&=& \log{\frac{P(\boldsymbol{x}|G_1)}{P(\boldsymbol{x}|G_2)}} - \log{\frac{P(G_2)}{P(G_1)}}
\quad・・・\quad(33)
\end{eqnarray}
$$
ここで、事前確率は $P(G_1) = \pi_1, P(G_2) = \pi_2$ なので、これを(33)式に代入すると、
$$
f(\boldsymbol{x})
= \log{\frac{P(\boldsymbol{x}|G_1)}{P(\boldsymbol{x}|G_2)}} - \log{\frac{\pi_2}{\pi_1}}
\quad・・・\quad(34)
$$
となって、テキストに書いてある補正項 $- \log{\pi_2/\pi_1}$ が出てきます。であれば、(34)式の右辺第1項の $\log{P(\boldsymbol{x}|G_1) / P(\boldsymbol{x}|G_2)}$ は、(26)式になるのでしょうか?テキストに書いてある(26)式の導出方法は、幾何学的なもので、確率的な要素は全く入っていません。参考文献 2 では、尤度 $P(\boldsymbol{x}|G_j)$ に多変量正規分布を仮定して(26)式を導いています。しかし、テキストでは群 $G_j$ のデータ生起過程に何ら分布は仮定していません。
これは、私の単なる妄想かもしれませんが、幾何学的に考えた場合でも、こういう風に考えてみるのはどうでしょう?(2)式で与えられる群 $G_j$ の標本平均 $\bar{\boldsymbol{x}}^{(j)}$ ですが、当然、これには誤差が含まれます。標本平均の標準誤差は $|\Sigma_j|/\sqrt{n_j}$ です。ここで、$\Sigma_j,n_j$ は、それぞれ、サンプル $\lbrace \boldsymbol{x_i} \rbrace_{i=1}^{n_j}$ の分散共分散行列、サンプル数です。つまり、標本平均は、両群の分散が同じ場合、サンプル数 $n_j$ の平方根の逆数に比例する曖昧さがあるというわけです。この曖昧さは、サンプル数 $n_j$ が小さくなると大きくなります。事前確率は $\pi_j = n_j / \sum_{j'=1}^{2} n_{j'}$ のようにサンプル数 $n_j$ と密接な関係があります。ただ、どうして補正項が両群のサンプル数の比の対数関数になるのかが説明できません。単なる比 $n_1/n_2 - 1$(あるいは $\pi_1/\pi_2 - 1$ )でもよいのではないかと思います。新しいサンプル $\boldsymbol{x}$ が、判別境界(Fig.3の緑色の破線)上にあれば、(26)式で与えられる判別関数は $0$ になるので、その場合に、サンプル数、ひいては事前確率によって、新しいサンプル $\boldsymbol{x}$ がどちらの群に属するか判別できればよいのですから、補正項が事前確率の比の対数である必要はないと思うのです。しかし、新しいサンプル $\boldsymbol{x}$ が判別境界の近傍にあるとき、事前確率の比の関数形(対数関数なのか単なる比なのか)がモノを言うのかもしれません。
【 補足:(31)式の証明 】
確率の乗法定理から
$$
P(\boldsymbol{x},G_j) = P(\boldsymbol{x}|G_j)P(G_j) = P(G_j|\boldsymbol{x})P(\boldsymbol{x})
\quad・・・\quad(35)
$$
が成り立ちます。(35)式を $P(G_j|\boldsymbol{x})$ について解くと
$$
P(G_j|\boldsymbol{x}) = \frac{P(\boldsymbol{x}|G_j)P(G_j)}{P(\boldsymbol{x})}
$$
となり、(31)式のベイズの定理を得る。
【コラム 補正項の解釈】
補正項の関数形の問題について考えてみました。下図は対数関数による補正項 $-\log{\frac{\pi_2}{\pi_1}}$ を描いたものです。横軸は事前分布の比 $\frac{\pi_1}{\pi_2}$ にとってあります。
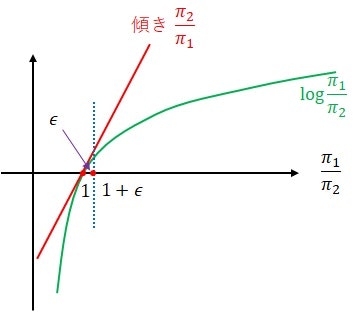
いま、$\frac{\pi_1}{\pi_2} \sim 1$ の近傍を考えてみます。$\epsilon \ll 1$ として、横座標上の $\frac{\pi_1}{\pi_2} = 1 + \epsilon$ の対数補正項を計算すると
$$
\log{\frac{\pi_1}{\pi_2}} = \log{(1 + \epsilon)} \sim \epsilon = \frac{\pi_1}{\pi_2}- 1
$$
となり、$- \log{\frac{\pi_2}{\pi_1}} = \frac{\pi_1}{\pi_2}- 1$ 、すなわち、$\frac{\pi_1}{\pi_2} \sim 1$ の近傍では、補正項の関数形は対数関数と単なる比が一致します。
マハラノビス平方距離による線形判別式の導出
テキストP.205の4行目から始まる第2段落では、(29)式で与えられるマハラノビス平方距離 $D^2$ をカスタマイズした、サンプル $\boldsymbol{x}$ と群 $G_j$ の標本平均 $\bar{\boldsymbol{x}}^{(j)}$ のマハラノビス平方距離 $D_j^2$ を使って(26)式と等価な(正確には $2f(\boldsymbol{x})$)判別関数が得られることを説明しています。テキストのこの部分の説明を以下に示します。
線形判別は共通の標本分散共分散行列 $S$ を用いて新しいサンプル $\boldsymbol{x}$ から群 $G_j$ の標本平均ベクトル $\bar{\boldsymbol{x}}^{(j)}$ までのマハラノビス平方距離 $ D_j^2 := \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(j)} \right) ^{\mathrm{T}} S^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(j)} \right) $ を計算すると、$D_2^2 - D_1^2 = 2f(\boldsymbol{x})$ なので、$D_2^2 > D_1^2$ なら $G_1$ に、$D_2^2 < D_1^2$ なら $G_2$ にサンプルを分類することと等価である。
これを証明しておきましょう。
$$
\begin{eqnarray}
D_2^2 - D_1^2
&=& \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(2)} \right) - \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(1)} \right) \\
&=& \left[ \boldsymbol{x} ^{\mathrm{T}} S^{-1} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \right] \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(2)} \right) - \left[ \boldsymbol{x} ^{\mathrm{T}} S^{-1} - \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \right] \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(1)} \right)\\
&=& \boldsymbol{x} ^{\mathrm{T}} S^{-1} \boldsymbol{x} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \boldsymbol{x} - \boldsymbol{x} ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} + \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} - \left[ \boldsymbol{x} ^{\mathrm{T}} S^{-1} \boldsymbol{x} - \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \boldsymbol{x} - \boldsymbol{x} ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} + \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} \right]\\
&=& \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \boldsymbol{x} + \boldsymbol{x} ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) + \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} - \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} \\
&=& 2 \boldsymbol{x} ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) - \left[ \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} \right] \\
&=& 2 \boldsymbol{x} ^{\mathrm{T}} \hat{\boldsymbol{w}} - \left[ \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} \right] \\
&=& 2 \hat{\boldsymbol{w}} ^{\mathrm{T}} \boldsymbol{x} - \left[ \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(1)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}}^{(2)} \right]
\quad・・・\quad(36)
\end{eqnarray}
$$
ここで、4行目から5行目に移るとき、4行目の第1項 $\left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \boldsymbol{x}$ はスカラーなので、転置しても変わらないため $ \left[ \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \boldsymbol{x} \right] ^{\mathrm{T}}= \boldsymbol{x} ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right)$ となることを用いました。さらに、5行目から6行目に移るとき、(24)式を用いました。
また、(25)式より
$$
\begin{eqnarray}
\hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(1)} + \hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(2)}
&=& \left( \bar{\boldsymbol{x}}^{(1)} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \left[ \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \right] \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(1)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(1)} +
\left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(2)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(2)} \\
&=& \left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(1)} - \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(2)}
\quad・・・\quad(37)
\end{eqnarray}
$$
となります。ここで、3行目から4行目へ移るとき、$ \left( \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(1)} =
\left( \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S^{-1} \bar{\boldsymbol{x}} ^{(2)} $ を用いました。スカラーは転置しても同じだからです。
(36)式と(37)式から
$$
\begin{eqnarray}
D_2^2 - D_1^2
&=& 2 \hat{\boldsymbol{w}} ^{\mathrm{T}} \boldsymbol{x} - \left( \hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(1)} + \hat{\boldsymbol{w}} ^{\mathrm{T}} \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& 2 \hat{\boldsymbol{w}} ^{\mathrm{T}} \boldsymbol{x} - \left( \bar{\boldsymbol{x}}^{(1)}-\bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S^{-1} \left( \bar{\boldsymbol{x}} ^{(1)} + \bar{\boldsymbol{x}} ^{(2)} \right) \\
&=& 2f(\boldsymbol{x})
\quad・・・\quad(38)
\end{eqnarray}
$$
が得られ、テキストに書いてあることが証明できました。ここで、1行目から2行目へ移るとき、(25)式を用い、2行目から3行目へ移るとき、(26)式を用いました。
2次判別分析
マハラノビス平方距離による線形判別式の導出を行ないましたが、(29)式で用いたのは共通の標本分散共分散行列 $S$ でした。ここでは、もっと直接的に、(10)式で与えられる群ごとの標本分散共分散行列 $S_j$ を用いる判別関数を求めます(テキストP.205の第3段落)。
まず、群ごとの標本分散共分散行列 $S_j$ を用いるマハラノビス平方距離を定義します。
$$
D_j^2
= \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(j)} \right) ^{\mathrm{T}} S_{j}^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(j)} \right)
\quad・・・\quad(39)
$$
これは、与えられたサンプル $\boldsymbol{x}$ と群 $G_j$ の標本平均 $\bar{\boldsymbol{x}}^{(j)}$ とのマハラノビス平方距離です。これを使えばもっとダイレクトに判別関数が得られます。つまり、サンプル $\boldsymbol{x}$ が、マハラノビス平方距離の意味で群 $G_1$ と群 $G_2$ のどちらに近いかを判定すればよいのです。したがって、この場合の判別関数は以下のようになります。
$$
\begin{eqnarray}
q(\boldsymbol{x})
&=& D_2^2 - D_1^2 \\
&=& \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(2)} \right) ^{\mathrm{T}} S_2^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(2)} \right) -
\left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(1)} \right) ^{\mathrm{T}} S_1^{-1} \left( \boldsymbol{x} - \bar{\boldsymbol{x}}^{(1)} \right)
\quad・・・\quad(40)
\end{eqnarray}
$$
そして、判別規則は次のようになります。
$$
\boldsymbol{x} の属する群 =
\begin{cases}
G_1 & ( q(\boldsymbol{x}) \gt 0 ) \\
G_2 & ( q(\boldsymbol{x}) \lt 0 )
\end{cases}
\quad・・・\quad(41)
$$
判別関数 $q(\boldsymbol{x})$ を2次判別関数とよびます。何故2次かというと、(40)式からも分かるように、判別関数が $\boldsymbol{x}$ の2次式になっているからです。それに対して(26)式で与えられるフィッシャーの線形判別関数は $\boldsymbol{x}$ の1次式です。また、判別境界の観点からいうと、フィッシャーの線形判別関数 $f(\boldsymbol{x})$ の判別境界はFig.3に示すように直線(1次関数)になりますが、2次判別関数 $q(\boldsymbol{x})$ の判別境界は後で示すように2次曲線(2次関数)になります。
線形判別分析と2次判別分析の違い
テキストP.205の第3段落の後半部分には、線形判別分析と2次判別分析の違いについての次の記述があります。
1次関数による線形判別分析と比較して柔軟な判別境界を表現することができる一方で、各クラスで異なる分散共分散行列を推定するため、サンプルサイズが小さい場合には数値的な不安定性が問題となったり、データへの過適合が生じる可能性が高くなることに注意が必要である。
まず、「サンプルサイズが小さい場合には数値的な不安定性が問題」となることについては直感的にも理解できると思います。「サンプル数に起因する判別関数の補正項」のところでも書いたように、一般に推定値のバラツキはサンプル数に依存し、サンプル数が少ないとバラツキが大きくなる傾向があります。したがって、計算結果が数値的に不安定になるのだと思います。
一方、「データへの過適合が生じる可能性が高くなる」ことについては自明ではありませんが、判別境界が直線ではなく2次曲線になるため、サンプル数が少ない場合、サンプルに鋭敏に反応して2次曲線の形が変わることを言っているのだと思います。
このことを検証するために、シミュレーションを行なってみました。まず、Fig.4に線形判別分析の結果(左側)と2次判別分析の結果(右側)を示します。

なお、このシミュレーションでは、群平均として $\bar{\boldsymbol{x}} ^{(1)} = (3,3), \hspace{4pt} \bar{\boldsymbol{x}} ^{(2)} = (-3,-3)$ を、また、群の分散共分散行列として $S_1 = \begin{pmatrix} 2 & -0.5 \\ -0.5 & 3 \end{pmatrix}, \hspace{4pt} S_2 = \begin{pmatrix} 3 & 0.3 \\ 0.3 & 1 \end{pmatrix}$ を、また、サンプル数として $n_1 = n_2 = 200$ を用いています。
Fig.4の右側から、2次判別分析の判別境界は2次曲線になっていることがわかります(右下に2次曲線から髭のようなものが出ているが、これはプログラムのバグによるものだと思われる)。次に、サンプル数を $5, 10, 20, 30, 40, 50$ と増やしながら2次判別境界を描いたものをFig.5に示します。

図から、サンプル数を変えると、判別境界がガラッと変わることが分かります(特にサンプル数を 5 から 10 に変えたとき)。このことからも、サンプル数が少ないときは、データに過適合していることがわかります(図中の直線等は、前述したようにプログラムのバグによるアーチファクトである)。
参考文献
- @pira:フィッシャーの線形判別分析法. https://qiita.com/pira/items/4c84399671be2cb598e4 (2023.9.9 確認)
- 東京大学大学院農学生命科学研究科 大森宏:判別分析. http://lbm.ab.a.u-tokyo.ac.jp/~omori/kensyu/discriminant.htm (2023.9.9 確認)
- ベイズの定理 とは?誰でも理解できるようにわかりやすく解説. https://www.headboost.jp/bayes-theorem/ (2023.9.9 確認)