オリジナル
基本例題8.33 P289 (pdf)<「材料力学演習(20221021)一括(ver.3.3)」を勉強したい。#sympy
???タブレット等で、pdfを開く事ができないかも。???
sympyで。単位荷重法で。
・(2024-12-16追加)
# p289 例題8.33
from sympy import *
EI,P1,P2,a,b,x =symbols('EI,P1,P2,a,b,x')
def myCollect(str,P1,P2):
return -collect((sympify(str).expand().simplify()),[P1,P2])
MAB_str="-a*P1-(a+b)*P2+(P1+P2)*x" ;print("#",MAB_str)
MBC_str=MAB_str +"-P1*(x-a)" ;print("#",MBC_str)
MAB =myCollect(MAB_str,P1,P2) #;print("#",MAB_str)
MBC =myCollect(MBC_str,P1,P2) #;print("#",MBC_str)
δ1 = 1/EI*Integral(-MAB*(-MAB.subs({P1:1,P2:0})),(x,0,a)) ;print("#",δ1)
δ2 =str(1/EI*Integral(-MAB*(-MAB.subs({P1:0,P2:1})),(x,0,a))) + "+" + \
str(1/EI*Integral(-MBC*(-MBC.subs({P1:0,P2:1})),(x,a,a+b))) ;print("#",δ2)
# -a*P1-(a+b)*P2+(P1+P2)*x
# -a*P1-(a+b)*P2+(P1+P2)*x-P1*(x-a)
# Integral((-a + x)*(P1*(-a + x) + P2*(-a - b + x)), (x, 0, a))/EI
# Integral((P1*(-a + x) + P2*(-a - b + x))*(-a - b + x), (x, 0, a))/EI+Integral(P2*(-a - b + x)**2, (x, a, a + b))/EI
sympyで。Castigliano's second theoremで。
・出力の順番。注意です。
# ver0.1
from sympy import *
EI,P1,P2,a,b,x =symbols('EI,P1,P2,a,b,x')
MAB_str="-a*P1-(a+b)*P2+(P1+P2)*x" #;print("#",MAB_str)
MBC_str=MAB_str +"-P1*(x-a)" #;print("#",MBC_str)
U = "1/(2*EI)*integrate((" + MAB_str+")**2,(x,0,a ))+" \
+"1/(2*EI)*integrate((" + MBC_str+")**2,(x,a,a+b))" #;print("#",U)
print("#",collect((diff(sympify(U),P1).expand()),[P1,P2]))
print("#",collect((diff(sympify(U),P2).expand()),[P1,P2]))
# P2*(a**3/(3*EI) + a**2*b/(2*EI)) + P1*a**3/(3*EI)
# P1*(a**3/(3*EI) + a**2*b/(2*EI)) + P2*(a**3/(3*EI) + a**2*b/EI + a*b**2/EI + b**3/(3*EI))
sympyで。モーメントのつりあいより。
微分方程式の直接解法で
The Myosotis Methodで
# ver0.3
from sympy import *
var('EI,P1,P2,a,b')
δ1 =(P2*b)*a**2/(2*EI)+(P1+P2)*a**3/(3*EI) ;print("#",δ1)
θ1 =(P2*b)*a / EI +(P1+P2)*a**2/(2*EI) ;print("#",θ1)
δ2d=P2*b**3/(3*EI) #;print("#",δ2d)
δ2 =factor(δ1+θ1*b+δ2d) ;print("#",δ2)
# P2*a**2*b/(2*EI) + a**3*(P1 + P2)/(3*EI)
# P2*a*b/EI + a**2*(P1 + P2)/(2*EI)
# (2*P1*a**3 + 3*P1*a**2*b + 2*P2*a**3 + 6*P2*a**2*b + 6*P2*a*b**2 + 2*P2*b**3)/(6*EI)
Castigliano's second theoremで。
# ver0.4
from sympy import *
EI,P1,P2,a,b,x =symbols('EI,P1,P2,a,b,x')
M01_str="-(P1*(a-x)+P2*(a+b-x))" ;print("#",M01_str)
M12_str= "-P2*(a+b-x)" ;print("#",M12_str)
U = "1/(2*EI)*integrate((" + M01_str+")**2,(x,0,a ))+" \
+"1/(2*EI)*integrate((" + M12_str+")**2,(x,a,a+b))" ;print("#",U)
δ1=collect((diff(sympify(U),P1).expand()),[P1,P2]) ;print("#",δ1)
δ2=collect((diff(sympify(U),P2).expand()),[P1,P2]) ;print("#",δ2)
# P2*(a**3/(3*EI) + a**2*b/(2*EI)) + P1*a**3/(3*EI)
# P1*(a**3/(3*EI) + a**2*b/(2*EI)) + P2*(a**3/(3*EI) + a**2*b/EI + a*b**2/EI + b**3/(3*EI))
割り込みでテスト2例
・以下は単体で、実行できません。ver0.4 の続き
# ver0.4 の続き
var('P,L')
rep={P1:P,a:L,P2:0,b:0}
print("#",δ1.subs(rep),diff(δ1.subs(rep),L))
rep={P1:4*P,a:L,P2:P,b:3*L}
print("#",δ1.subs(rep),diff(δ1.subs(rep),L))
print("#",δ2.subs(rep),diff(δ2.subs(rep),L))
# L**3*P/(3*EI) L**2*P/EI
# 19*L**3*P/(6*EI) 19*L**2*P/(2*EI)
# 86*L**3*P/(3*EI) 86*L**2*P/EI
(旧)sympyのBeamで。作図だけ。
# ver0.5
from sympy import *
from sympy.physics.continuum_mechanics.beam import Beam
from sympy import symbols
E,I,RO,RA,PB=symbols('E,I,RO,RA,PB')
a,b =symbols('a,b',positive=True)
var("x,P1,P2")
# def myBeam_Katamoti_RP_Tawami(a,b,E,I,PB):
# b=Beam(a+b,E,I)
# b.apply_load( RO,0, -1)
# b.apply_load( RA,a ,-1)
# # b.apply_load(-PB,a+b,-1)
# b.apply_load(-PB,2,-1)
# b.bc_deflection.append((0,0))
# b.bc_deflection.append((a,0))
# b.bc_slope .append((0,0))
# b.solve_for_reaction_loads(RO,RA)
# return b.deflection()
def myBeam_Katamoti_P1P2_Sakuzu(a,b,E,I,P1,P2):
b=Beam(a+b,E,I)
# b.apply_load(PB,a+b,-1) # error
b.apply_load (P1,0.75,-1)
b.apply_load (P2,1.00,-1)
b.apply_support(0,'fixed')
p = b.draw()
p.show()
return
# δ =myBeam_Katamoti_RP_Tawami(a,b,E,I,PB)
myBeam_Katamoti_P1P2_Sakuzu (0.75,0.25,1,1,1,1)
sympyのBeamで。計算と作図。
・作図データの値は、1です。
・教えて下さい。目盛りの数字を非表示方法。
# ver0.6
from sympy.physics.continuum_mechanics.beam import Beam
from sympy import *
var('E,I')
var('P1,P2,RA,MA,x')
var('la,lb',positive=True) # positive が必要です。
var('P1_2,P2_2,RA_2,MA_2')
var('la_2,lb_2',positive=True) # positive が必要です。
def val_P1P2_Cantilever_Draw(P1_2,P2_2,la_2,lb_2,E_2,I_2):
la_2,lb_2,P1_2,P2_2,E_2,I_2=1,1,1,1,1,1
b_2=Beam(la_2+lb_2,E_2,I_2)
b_2.apply_load(P1_2,la_2 ,-1)
b_2.apply_load(P2_2,la_2+lb_2,-1)
#
b_2.bc_slope =[(0,0)]
b_2.bc_deflection=[(0,0)]
b_2.apply_load(RA_2,0,-1)
b_2.apply_load(MA_2,0,-2)
b_2.solve_for_reaction_loads(RA_2,MA_2)
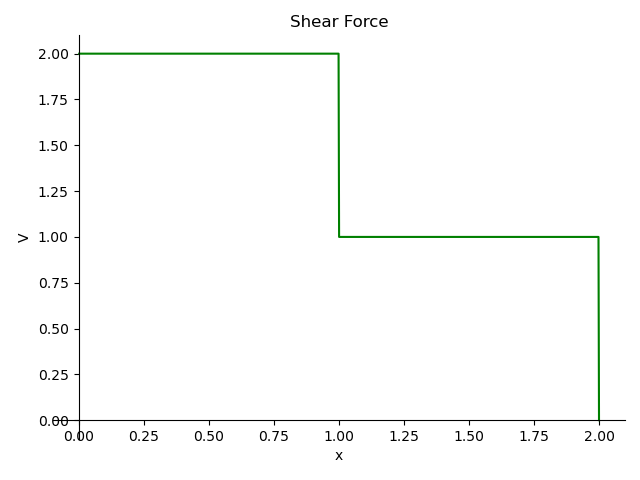
b_2.plot_shear_force()
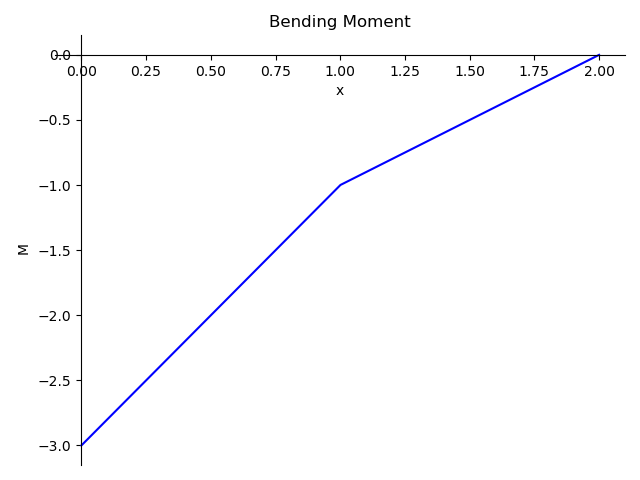
b_2.plot_bending_moment()
# remove_support が無いため、順番固定です。plot_shear_force,plot_bending_moment() → draw().show()
b_2.remove_load(RA_2,0,-1)
b_2.remove_load(MA_2,0,-2)
b_2.apply_support( 0,"fixed")
b_2.draw().show()
return b_2
def my_P1P2_Cantilever_Cal(P1,P2,la,lb,E,I):
b=Beam(la+lb,E,I)
b.apply_load(RA,0 ,-1)
b.apply_load(MA,0 ,-2)
b.apply_load(P1,la ,-1)
b.apply_load(P2,la+lb,-1)
b.bc_slope =[(0,0)]
b.bc_deflection=[(0,0)]
return b
# ----------------------------------------------------------------------------------------------
b=my_P1P2_Cantilever_Cal(P1,P2,la,lb,E,I)
b.solve_for_reaction_loads(RA,MA)
print("#",Poly(b.deflection().subs({x:la+lb}),P1,P2).args[0])
# 例1
var('P,l')
rep_Rei={la:l/2,lb:l/2}
print("#",b.deflection().subs({x:la+lb}).subs(rep_Rei))
# 例2
rep_Rei={P1:P,P2:P,la:l/2,lb:l/2}
print("#",b.deflection().subs({x:la+lb}).subs(rep_Rei))
# ----------------------------------------------------------------------------------------------
# 作図
c=val_P1P2_Cantilever_Draw(P1,P2,la,lb,E,I)
# P1*(2*la**3 + 3*la**2*lb)/(6*E*I) + P2*(la**3 + 3*la**2*lb + 3*la*lb**2 + lb**3)/(3*E*I)
# -(-5*P1*l**3/48 - P2*l**3/3)/(E*I)
# 7*P*l**3/(16*E*I)
いつもの? sympyの実行環境と 参考のおすすめです。
いつもと違うおすすめです。
・荷重が1個の場合
wikipedia
「弾性曲線方程式の様々な表示」 の表< 各諸量とたわみの関係 < wikipedia
・上記の英語版は、見つける事ができませんでした。
参考文献
>Fig.5.46 The cantilever beam subjected with the two concentrated forces.
【練習問題】【5.14】
JSME 演習 p65
>単純支持ばり 7)
>構造力学公式集 p136