2つの円の共通接線「ラ・サール高校 伝説の問題 線分AB＝？」をsympyとFreeCADでやってみたい。

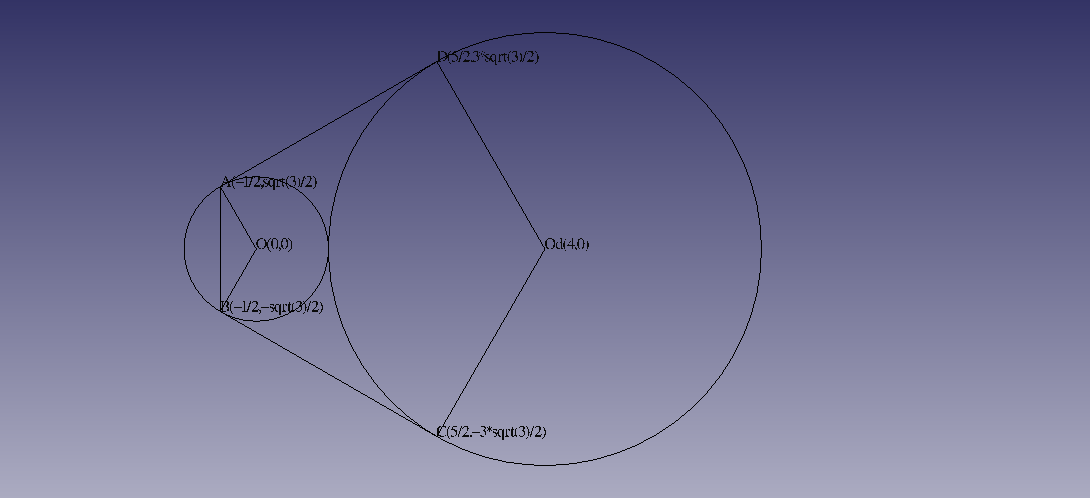
・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面上に作図しました。
・座標変換(Homogeneous coordinates)もあります。

オリジナル

・YUUU0123 様 (0:00〜4:58)

sympyで(オリジナル 様の方法を参考に)

ver0.1 ＞これは、長方形になりますので...

# ver0.1 ＞これは、長方形になりますので...
from sympy import *
r,rd=1,3
FB=sqrt((1+3)**2-(3-1)**2)/2
print("#",FB)
# sqrt(3)

sympyで(いつもの方法で)

ver0.2　円と円の交点計算です。三平方の定理の代わり。

・原点O,x軸方OO'(点名Odとします）です。
・OEを90°回転。単位ベクトル1進むです。
rotate(angle, pt=None)
Rotate angle radians counterclockwise about Point pt.
https://docs.sympy.org/latest/modules/geometry/points.html#sympy.geometry.point.Point2D.rotate

# ver0.2 円と円の交点計算です。三平方の定理の代わり。
from sympy import *
r,rd=1,3
O,Od=map(Point,[(0,0),(r+rd,0)])
OE  =sqrt((r+rd)**2-(rd-r)**2) 
E   =Circle(O,OE).intersection(Circle(Od,rd-r))[1]   
B   =E.unit.rotate(-pi/2)
print("#",B.y*(-2))
# sqrt(3)

ver0.3 座標変換です。角度計算がオモテに現れないけど、難しい。

# ver0.3 座標変換です。角度計算がオモテに現れないけど、難しい。
from sympy import *
var('t,Tx,Ty',real=true)
r,rd=1,3
OE  =sqrt((r+rd)**2-(rd-r)**2) 
O , Od=map(Matrix,([[0],[0],[1]],[[r+rd],[0] ,[1]]))
sO,sOd=map(Matrix,([[0],[r],[1]],[[OE]  ,[rd],[1]]))
myMat =    Matrix([[ cos(t),-sin(t),Tx],
                   [ sin(t), cos(t),Ty],
                   [0      ,0     ,1 ]])
sol=solve([Eq(myMat*sO,O),Eq(myMat*sOd,Od)],[t,Tx,Ty])
print("#",-sol[0][2]*2)
# sqrt(3)

ver0.4 自作三角形の連結です。内部で座標変換です。ver0.3と同じ。

・直角三角形２つの連結です。積み木です。
https://qiita.com/mrrclb48z/items/eda67f399965ea64df89
・プログラミングは、新規2行?です。無理すれば1行です。

# ver0.4 自作三角形の連結です。内部で座標変換です。ver0.3と同じ。
from sympy import *
def myMatrixToPoint(myMatrix):    
    return Point2D(myMatrix[0],myMatrix[1])
def myPoinrToMatrix(myPoint):    
    return Matrix([[myPoint.x],[myPoint.y],[1]]) 
def myTr02(tr1,tr2):
    t     =Line(tr1.args[0],tr1.args[0]+Point(1,0)).angle_between(Line(tr1.args[0],tr1.args[2]))
    myTurn=Matrix([[cos(t),-sin(t),tr1.args[0].x],[sin(t),cos(t),tr1.args[0].y],[0,0,1]])
    return Triangle(myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[0])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[1])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[2])))

r,rd=1,3
print("#",myTr02(Triangle(sss=(r+rd,rd-r,sqrt((r+rd)**2-(rd-r)**2))) ,Triangle(sas=(1,90,r))).args[2].y*2)
# sqrt(3)

FreeCADのマクロで作図

・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面に作図しました。
・計算部分は、Ver.0.2 の コピー貼り付けです。

import FreeCAD
import Part
import DraftTools
import Draft
import Mesh
############################################################################
# ver0.2 ラサール　円と円の交点計算です。三平方の定理の代わり。
from sympy import *
r,rd=1,3
O,Od=map(Point,[(0,0),(r+rd,0)])
OE  =sqrt((r+rd)**2-(rd-r)**2) 
E   =Circle(O,OE).intersection(Circle(Od,rd-r))[1]   
B   =E.unit.rotate(-pi/2)
print("#",B.y*(-2))
# sqrt(3)
############################################################################
C=Od+rd*(E-Od).unit
A=Point(B.x,-B.y)
D=Point(C.x,-C.y)
############################################################################
# 3D作図 z=0 XY平面に作図しました。
############################################################################
# 円の作図　FrecCADのdocより
# https://wiki.freecad.org/Macro_Circle
def Freecad3D_circle(x=0.0,y=0.0,z=0.0,radius=0.0,diameter=0.0,circumference=0.0,area=0.0,startangle=0.0,endangle=0.0,arc=0.0,anglecenter=0.0,cord=0.0,arrow=0.0,center=0,placemObject=""):
    from math import sqrt, pi
    if placemObject == "":
        pl = FreeCAD.Placement()
        pl.Rotation = FreeCADGui.ActiveDocument.ActiveView.getCameraOrientation()   
        pl.Base = FreeCAD.Vector(x,y,z)
    else:
        pl = FreeCAD.Placement()
        pl = placemObject                                  # placement imposted
    if diameter != 0:                                      # with diameter
        radius = diameter / 2.0
    elif circumference != 0:                               # with circumference
        radius = (circumference / pi) / 2.0
    elif area != 0:                                        # with area
        radius =  sqrt((area / pi))
    elif (cord != 0) and (arrow != 0):                     # with cord and arrow
        radius = ((arrow**2) + (cord**2) / 4.0) / (arrow*2) 
    elif (arc != 0) and (anglecenter != 0):                # with arc and anglecenter central in degrees
        radius = ((360/anglecenter)*arc) / pi/2.0
        if endangle != 0:
            startangle  = endangle - anglecenter
        endangle   = anglecenter + startangle
        startangle  = endangle - anglecenter
    if radius != 0:
        try:
            Draft.makeCircle(radius,placement=pl,face=False,startangle=startangle,endangle=endangle,support=None)
            if center != 0:
                x=pl.Base.x
                y=pl.Base.y
                z=pl.Base.z
                Draft.makePoint(x,y,z)
        except Exception:
            App.Console.PrintError("Unexpected keyword argument" + "\n")
        App.ActiveDocument.recompute()
    else:
        App.Console.PrintMessage("Unexpected keyword argument" + "\n")
        App.Console.PrintMessage("circle(x,y,z,radius,diameter,circumference,area,startangle,endangle,[arc,anglecenter],[cord,arrow],center,placemObject)" + "\n")
        App.Console.PrintMessage("circle(radius=10.0,placemObject=App.Placement(App.Vector(11,20,30), App.Rotation(30,40,0), App.Vector(0,0,0)))" + "\n")
    return
def myCircle_2D(myCi):
    x=myCi.center.x
    y=myCi.center.y
    r=myCi.radius
    Freecad3D_circle(
           x=float(x),y=float(y),z=0.0,
           radius=float(abs(r)),
           center=1,
           placemObject=App.Placement(App.Vector(float(x),float(y),0),
           App.Rotation(0,0,0),App.Vector(0,0,0)))
    return
def myXYZ2Txt_2D(A):
    return ""
def myXYZ2Txt_XY_2D(A):
    return '(' + str(A.x) + ',' + str(A.y) +  ')'
def myTxtXYZ_2D(A,myWedgei):
    P5x=float(A.x)
    P5y=float(A.y)
    P5z=0.0
    p5 = FreeCAD.Vector(P5x, P5y, P5z)
    myText = Draft.makeText(myWedgei, p5)
    myText.Label = myWedgei
    FreeCADGui.ActiveDocument.ActiveObject.FontSize = '0.2 mm'
    # FreeCADGui.ActiveDocument.ActiveObject.FontSize = '1.0 mm'
    # FreeCADGui.ActiveDocument.ActiveObject.FontSize = '0.5 mm'
    return
def myTxtXYZ_S_2D(*xy_tx):
    for i in range(1,int(len(xy_tx)/2)+1):
        myTxtXYZ_2D(xy_tx[2*i-2],xy_tx[2*i-1]+myXYZ2Txt_2D(xy_tx[2*i-2]) )
    return
def myTxtXYZ_XY_S_2D(*xy_tx):
    for i in range(1,int(len(xy_tx)/2)+1):
        myTxtXYZ_2D(xy_tx[2*i-2],xy_tx[2*i-1]+myXYZ2Txt_XY_2D(xy_tx[2*i-2]) )
    return
def myLine_2D(A,B):
    Ax,Ay,Az=float(A.x),float(A.y),0.0
    Bx,By,Bz=float(B.x),float(B.y),0.0
    pl = FreeCAD.Placement()
    pl.Rotation.Q = (0.4247081540122249, 0.17592004639554645, 0.33985110062924484, 0.8204732460821097)
    pl.Base = FreeCAD.Vector(-3.9166066876399563, -2.1670824762243774, 1.7495260956243028)
    points = [FreeCAD.Vector(Ax,Ay,Az), FreeCAD.Vector(Bx,By,Bz)]
    line = Draft.make_wire(points, placement=pl, closed=False, face=True, support=None)
    Draft.autogroup(line)
    return
def myLine_S_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    return
def myLine_C_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    myLine_2D(args[i],args[0])
    return
def myLine_H_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[0],args[i])
    return
##################################################################################
myLine_S_2D     (D,A,B,C)  
myLine_S_2D     (A,O ,B)  
myLine_S_2D     (C,Od,D)  
myTxtXYZ_XY_S_2D(O ,"O" )
myTxtXYZ_XY_S_2D(Od,"Od")
myTxtXYZ_XY_S_2D(A,"A",B,"B",C,"C",D,"D")
myCircle_2D     (Circle(O ,r ))
myCircle_2D     (Circle(Od,rd))
####################################################################################
doc = App.activeDocument()
#App.ActiveDocument.addObject("App::Origin", "Origin")
#App.ActiveDocumen!t.getObject('Origin').Visibility = True
App.ActiveDocument.recompute()
Gui.activeDocument().activeView().viewAxonometric()
Gui.SendMsgToActiveView("ViewFit")

isometric方向?です。(省略)
拡大図

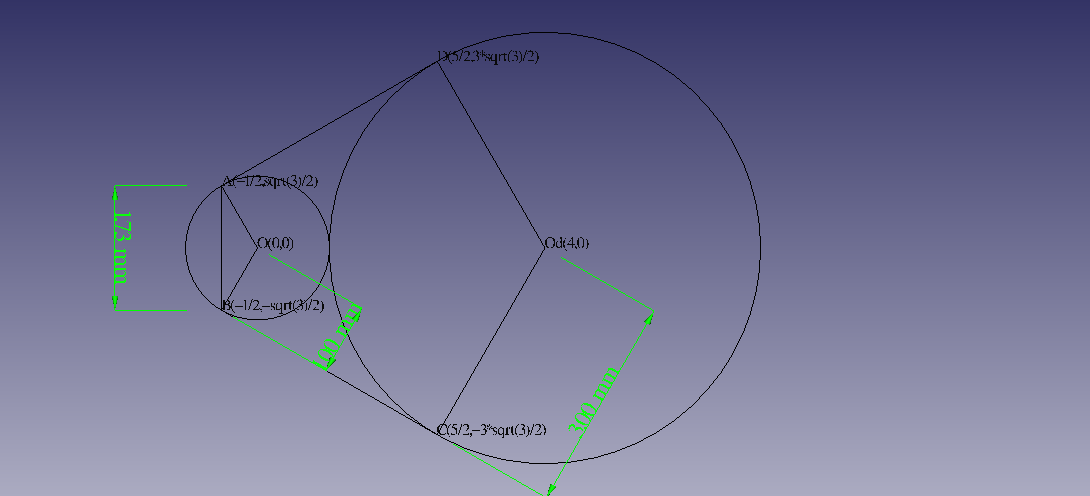
拡大図(CADの操作で寸法線を追加)
・(青色の)角度寸法は、ニセモノです。Part＞計測＞角度計算 です。
・角度寸法の表示は、まだ勉強中です。

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

・以下ができたら、助かります。指定と全部です

いつもと違うおすすめです。