>等式制約付きの関数最大化・最小化問題
・何も「ラグランジュの未定乗数法」を使わなくても?です。
別解という事でよろしくお願いします。
・WolframAlphaで3Dプロットがでます。
オリジナル
高校数学の美しい物語 様より 三変数のラグランジュ関数
ChatGPTで(xxxラグランジュの未定乗数法で、できませんでした。xxx) できました。
入力文
x2+y2=1のもとで 2x+3yの最大値、最小値をラグランジュの未定乗数法を使ってもとめよ.
>..したがって、制約条件x^2 + y^2 = 1の下で2x + 3yの最大値は13/2で、最小値は-13/2です。
すばらしいです。答えが違うけど、どこが?違うかわからない。
x2+y2=1のもとで 2x+3yの最大値、最小値をもとめよ.
>...この問題は、ラグランジュの未定乗数法を使用する必要はありません。
>...したがって、制約条件 x^2 + y^2 = 1 の下で、2x + 3y の最大値は √13 であり、最小値は -√13 です。
つづき?会話になっています。
すばらしいです。答えも正解です。 私がこう言えるのも今だけでしょうか?
Mathematicaで
勉強中。Mathematicaならではです。
WolframAlphaで(いつも?のやつ)
・ラグランジュの未定乗数法を使っていません。
・WolframAlphaで3Dプロットがでます。
結果 すばらしいです。
sympyで(高校数学の美しい物語 様の方法を参考に)
ラグランジュの未定乗数法で
from sympy import *
var('x,y',real=True)
var('λ,L',real=True)
eq=Eq(x**2+y**2,1)
f =2*x+3*y
L=f-λ*(eq.lhs-eq.rhs)
#
eq_dLdx=Eq(diff(L,x),0)
eq_dLdy=Eq(diff(L,y),0)
eq_dLdλ=Eq(diff(L,λ),0)
eq_dxdy=Eq(x,solve( Eq(solve(eq_dLdx,λ)[0],
solve(eq_dLdy,λ)[0]),x)[0])
ans=solve( [eq_dxdy,eq_dLdλ],[x,y] )
#
print("#",eq_dxdy)
print("#",ans[0])
print("#",ans[1])
print("#",f.subs({x:ans[0][0],y:ans[0][1]} ))
print("#",f.subs({x:ans[1][0],y:ans[1][1]} ))
# Eq(x, 2*y/3)
# (-2*sqrt(13)/13, -3*sqrt(13)/13)
# (2*sqrt(13)/13, 3*sqrt(13)/13)
# -sqrt(13)
# sqrt(13)
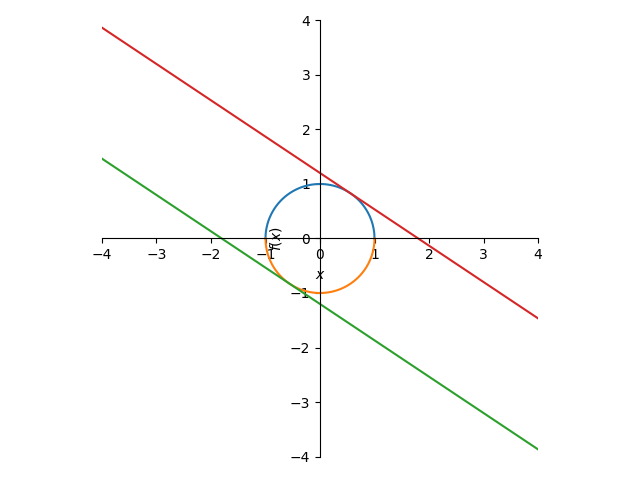
sympyで(いつものx+y=kで)Plot Moduleで作図
ラグランジュの未定乗数法を使っていません。
minimum,maximum関数です。
from sympy import *
var('x,y,k',real=True)
eq =Eq(x**2+y**2,1 )
eqk =Eq(k ,2*x+3*y)
#
y_ans=solve(eq,y)
k0 =eqk.rhs.subs({y:y_ans[0]})
k1 =eqk.rhs.subs({y:y_ans[1]})
k0_min=minimum(k0,x,Interval(-1,1))
k0_max=maximum(k0,x,Interval(-1,1))
k1_min=minimum(k1,x,Interval(-1,1))
k1_max=maximum(k1,x,Interval(-1,1))
print("#",solveset(Eq(k0,k0_min),x,Interval(-1,1)).args[0],k0_min)
print("#",solveset(Eq(k1,k1_max),x,Interval(-1,1)).args[0],k1_max)
# -2*sqrt(13)/13 -sqrt(13)
# 2*sqrt(13)/13 sqrt(13)
l0=solve( Eq(k0_min,eqk.rhs),y)[0]
l1=solve( Eq(k1_max,eqk.rhs),y)[0]
(st,en)=(-4,4)
p1=plot(sqrt(1-x**2),-sqrt(1-x**2),(x,-1,1), aspect_ratio=(1.0,1.0),xlim=(st,en),ylim=(st,en),show=False)
p2=plot(l0 ,(x,st,en), aspect_ratio=(1.0,1.0),show=False)
p3=plot(l1 ,(x,st,en), aspect_ratio=(1.0,1.0),show=False)
p1.extend(p2)
p1.extend(p3)
p1.show()
sympyで(微分で)
勉強中です。
sympyで(sin,cosで)
勉強中です。
sympyで(図形的に)
勉強中です。
sympyの実行環境
①私の環境は,pycharmです。
②よく聞くのは、Jupyterです。
③web上で、上記のソースを「SymPy Live shell」に、コピー貼り付けでもできました。
黒背景の右上に、マウスを移動すると、コピーマークが発生します。
??? タブレット環境で、コピー貼り付けが実行できませんでした。???
参考
wikipedia
2次元の場合<
以下、いつもの?おすすめです。