sinθ^3-cos^3「2021 青森公立大学前期 経営経済学部【１】問題1」をChatGPTとWolframAlphaとsympyでやってみたい。

・WolframAlphaとsympyで,グラフがでます。
・??? -(-sin(θ) + cos(θ)) ---> x 左の置き換えができません。???

オリジナル　
T氏の数学日記 様

数学入試問題 様

上と同じです。大学入試数学問題集成＞テキスト【１】問題1

公式ホームページ 2019年度〜2023年度入学者選抜

xxx ChatGPTで(できませんでした。) xxx

入力文

sinθ−cosθ=xとする．このとき，次の式をxで表せ．
sinθ^3−cos3θ^3

＞これを展開して簡略化することも可能ですが、式が非常に複雑になるため、...

xxx WolframAlphaで(できませんでした）xxx

＞代入しただけ

sympyで（1)T氏の数学日記 様の同値変形のやり方を参考に

??? -(-sin(θ) + cos(θ)) ---> x 置き換えができなかったので、???
??? factor_list関数で分解して，対応しました。???
いつの日か、ユーザー定義関数をつくってみたい。

from sympy import *
x,θ,y=symbols('x,θ,y',real=True)
Subs={sin(θ)**2+cos(θ)**2:1}
myEq_x=Eq(x,sin(θ)-cos(θ))                                                           ;print("#x",myEq_x)
myEq_y=Eq(y,sin(θ)**3-cos(θ)**3)                                                     ;print("#y",myEq_y)# 
# 
myEq_1=Eq(myEq_x.lhs**2,(myEq_x.rhs**2).expand().subs(mySubs))                       ;print("#1",myEq_1)
myEq_2=Eq(sin(θ)*cos(θ),solve(myEq_1,sin(θ)*cos(θ))[0])                               ;print("#2",myEq_2)
# ?????????  -(-sin(θ) + cos(θ))  ----> x
# print(           factor(myEq_y.rhs)                              )
# myEq_3=Eq(myEq_y,factor(myEq_y.rhs).subs({myEq_x.rhs:myEq_x.lhs}))                   ;print("#3",myEq_3)
# 
myList=factor_list(myEq_y.rhs)
myList=(myList[0]*myList[1][0][0]).subs({myEq_x.rhs:myEq_x.lhs})*myList[1][1][0]
myEq_3=Eq(myEq_y.lhs,myList)                                                         ;print("#3",myEq_3)
# 
myEq_4=Eq(myEq_y.lhs,myEq_3.rhs.subs({myEq_2.lhs:myEq_2.rhs}).subs(mySubs).expand()) ;print("#4",myEq_4)
#x Eq(x, sin(θ) - cos(θ))
#y Eq(y, sin(θ)**3 - cos(θ)**3)
#1 Eq(x**2, -2*sin(θ)*cos(θ) + 1)
#2 Eq(sin(θ)*cos(θ), 1/2 - x**2/2)
#3 Eq(y, x*(sin(θ)**2 + sin(θ)*cos(θ) + cos(θ)**2))
#4 Eq(y, -x**3/2 + 3*x/2)

sympyで（2)θの逆関数で

from sympy import *
x,θ=symbols('x,θ',real=True)
myEq=Eq(x,sin(θ)-cos(θ))
y   =sin(θ)**3-cos(θ)**3
θ_ans=solve(myEq,θ)
print("#",θ_ans)
print("#",y.subs({θ:θ_ans[0]}).simplify().expand() )
print("#",y.subs({θ:θ_ans[1]}).simplify().expand() )
# 
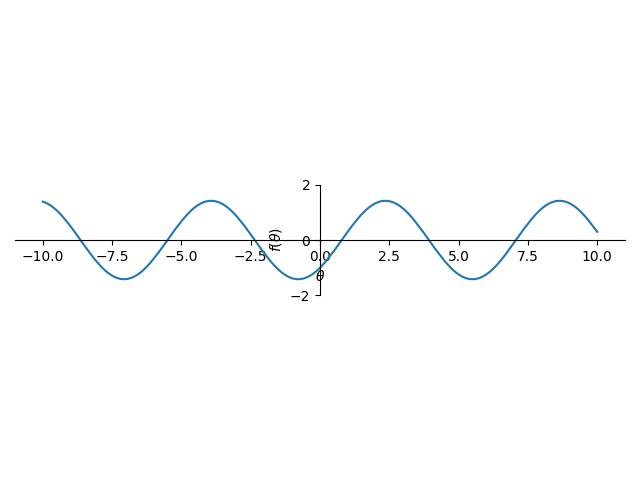
plot(myEq.rhs          ,aspect_ratio=(1.0,1.0)            ,ylim=(-2,2))
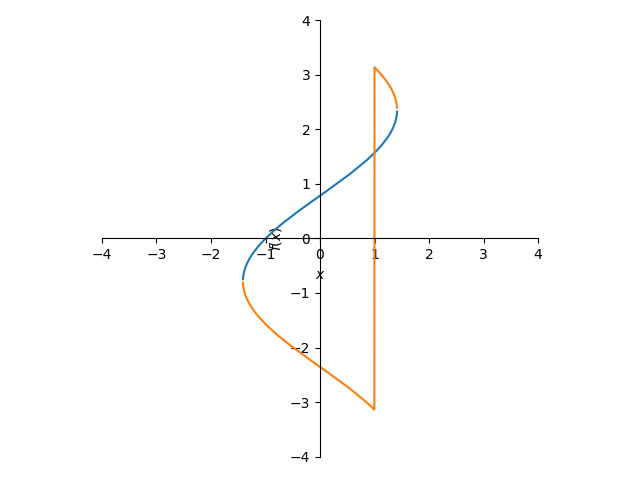
plot(θ_ans[0],θ_ans[1] ,aspect_ratio=(1.0,1.0),xlim=(-4,4),ylim=(-4,4))
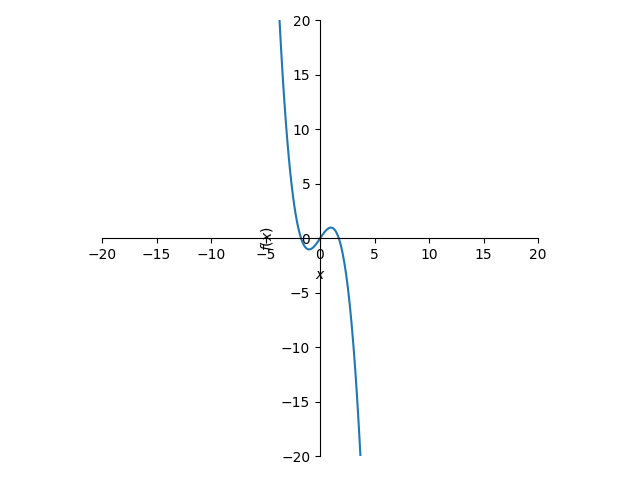
plot(y.subs({θ:θ_ans[0]}).simplify().expand(),(x,-4,4),aspect_ratio=(1.0,1.0),xlim=(-20,20),ylim=(-20,20))
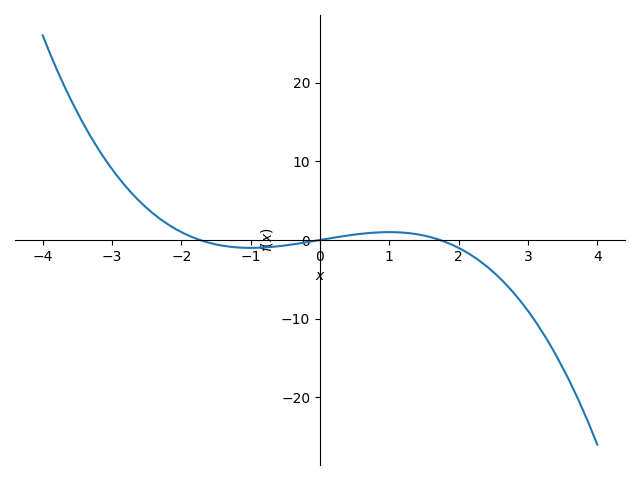
plot(y.subs({θ:θ_ans[0]}).simplify().expand(),(x,-4,4) )
# [-2*atan((sqrt(2 - x**2) - 1)/(x - 1)), 2*atan((sqrt(2 - x**2) + 1)/(x - 1))]
# -x**3/2 + 3*x/2
# -x**3/2 + 3*x/2

θ-x

x-θ

x-y

(詳細)x-y

sympyで（3)θの合成の逆関数で

from sympy import *
# from sympy.simplify.fu import TR9
x,θ=symbols('x,θ',real=True)
myEq  =Eq(x,sin(θ)-cos(θ))
y     =sin(θ)**3-cos(θ)**3
myEq1 =Eq(x,trigsimp( myEq.rhs ))
θ_ans1=solve(myEq1,θ);
# 
print("#",myEq1 )
print("#",θ_ans1)
print("#",y.subs({θ:θ_ans1[0]}).simplify().expand() )
print("#",y.subs({θ:θ_ans1[1]}).simplify().expand() )
# 
plot(myEq1.rhs           ,aspect_ratio=(1.0,1.0)            ,ylim=(-2,2))
plot(θ_ans1[0],θ_ans1[1] ,aspect_ratio=(1.0,1.0),xlim=(-4,4),ylim=(-4,4))
# Eq(x, -sqrt(2)*cos(θ + pi/4))
# [-acos(-sqrt(2)*x/2) + 7*pi/4, acos(-sqrt(2)*x/2) - pi/4]
# -x**3/2 + 3*x/2
# -x**3/2 + 3*x/2

θ-x

x-y 不思議？？？

sympyの実行環境

①私の環境は,pycharmです。
②よく聞くのは、Jupyterです。
③web上で、上記のソースを「SymPy Live shell」に、コピー貼り付けでもできました。
黒背景の右上に、マウスを移動すると、コピーマークが発生します。
???　タブレット環境で、コピー貼り付けが実行できませんでした。???

参考

以下、いつもの?おすすめです。